Министерство образования Российской Федерации
Уральский Государственный Технический Университет
филиал г. Краснотурьинска.
Тема: «Линейные электрические цепи постоянного тока. Линейные магнитные цепи».
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №1.
Руководитель Федотова Л. А.
Студент Боярских А. О.
Группа Э-2132
г. Краснотуринск
2002 г.
Вариант 52.
Задача 1.1: Анализ линейной цепи постоянного тока.
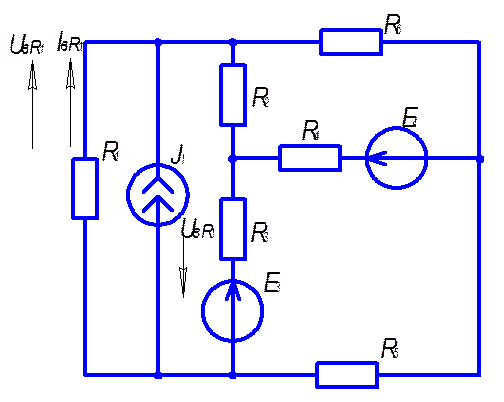 Дано:
Дано:
R1=6 ОМ; Е3=8 В;
R2=16 ОМ; Е4=12 В;
R3=2 ОМ; J1=1 A;
R4=4 ОМ; R5=8 ОМ;
R6=10 ОМ;
1. Анализ по методу контурных токов:
1.1. Преобразование источника тока в эквивалентный источник ЭДС.
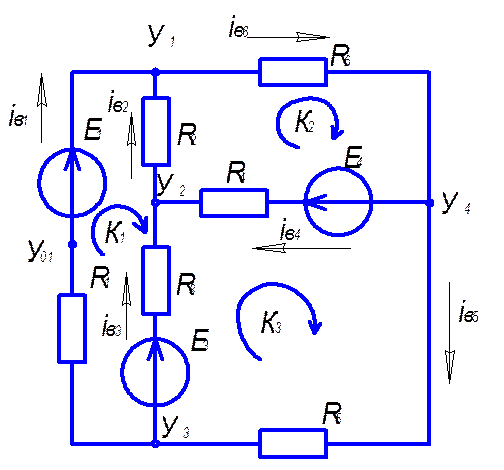 Е1=J1∙R1=1∙6=6 В
Е1=J1∙R1=1∙6=6 В
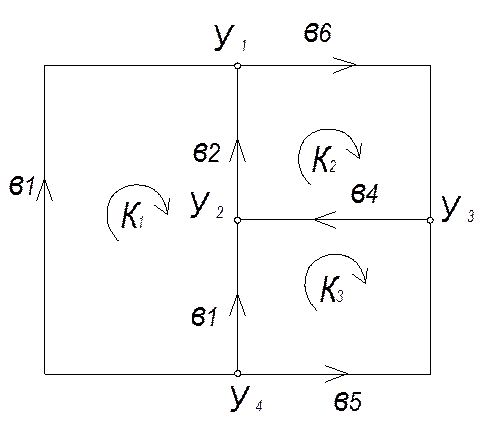
к=4; n=6;
n1=к-1=3; n2=n-n1=3;
Дерево графа: в2, в4, в3;
Связи графа: в1, в5,
в6;
1.2. Расчет полученной схемы методом контурных токов.
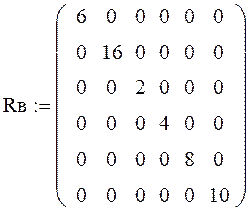
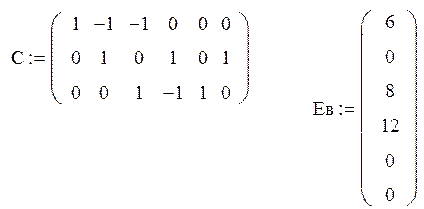
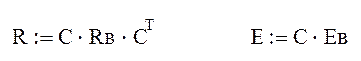
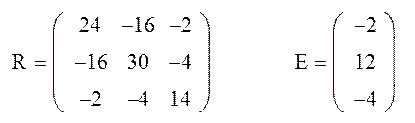
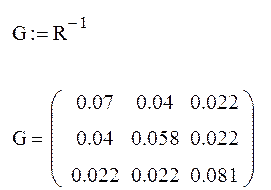
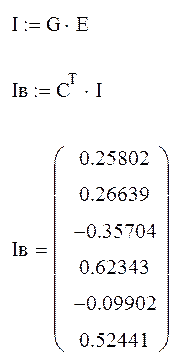
1.3. Определение напряжений каждого участка схемы.
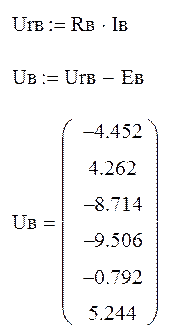
1.4. Проверка полученного решения по законам Кирхгофа.
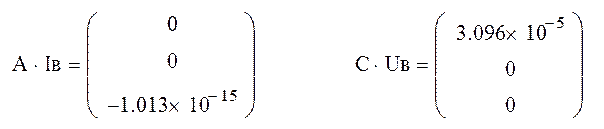
1.5. Составление баланса мощностей в исходной схеме (в схеме с источником тока).
IвR1=Iв1-J1=-0742 А
UвR1= IвR1∙R1=-4,452 В
PJ1=-J1∙R1=4,452 Вт
E3∙I3+E4∙I4+PJ1=IвR12∙R1+ Iв22∙R2+ Iв62∙R6+ Iв32∙R3+ Iв42∙R4+ Iв52∙R5
9,077=9,077
2. Расчет токов методом узловых потенциалов.
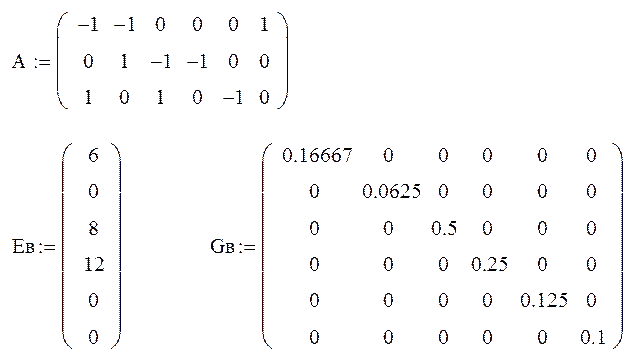
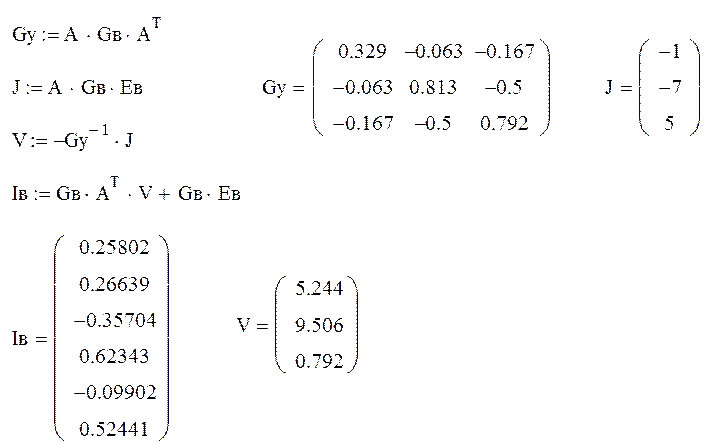
3. Изображение схемы с указанием истинных направлений токов.
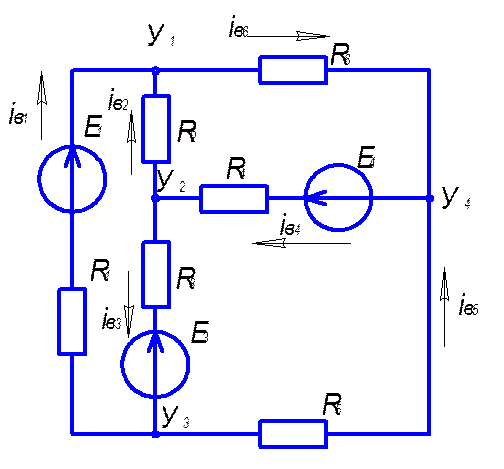
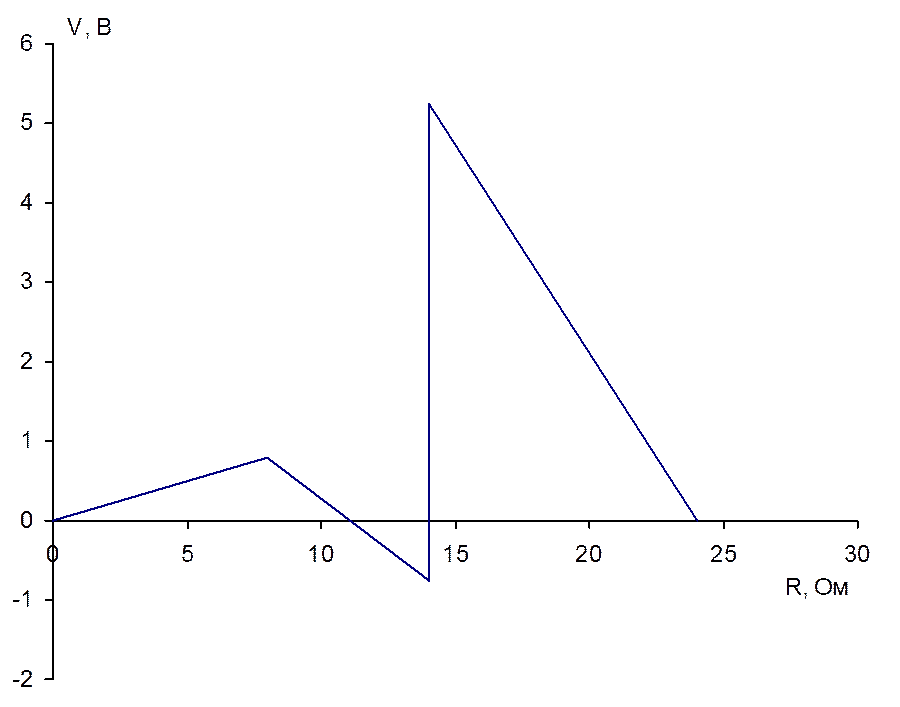
4. Построение потенциальной диаграммы для наружного контура.
V1=5,244 В; V3=0,792 В;
V4=0 В; V01=V3-Iв1∙R1=-0,75594 В;
R=R1+R5+R6=6+8+10=24 Ом.
5. Определение тока в третьей ветви методом эквивалентного генератора.
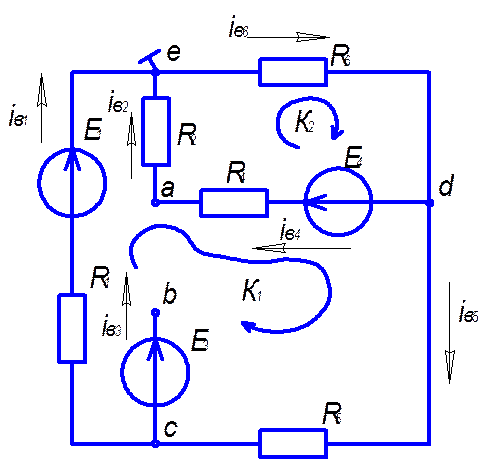 Iк1∙(R4+R2+R6)- Iк2∙(R4+R2)=E4
Iк1∙(R4+R2+R6)- Iк2∙(R4+R2)=E4
Iк2∙(R4+R2+R6)-Iк1∙(R4+R2)=E1-E4
![]() 30∙ Iк1-20∙ Iк2=12
30∙ Iк1-20∙ Iк2=12
36∙ Iк2-20∙ Iк1=-6
Iк1=0,4588 А
Iк2=0,088 А
I= Iк1- Iк2=0,3708 F
Va=Ve+I∙R2=5,9328 В
Vd=Ve- Iк1∙R6=-4,588 В
Vc=Vd- Iк2∙R5=-5,292 В
Vb=Vc+E3=2,708 В
Vab=Va-Vb=3,2248 В

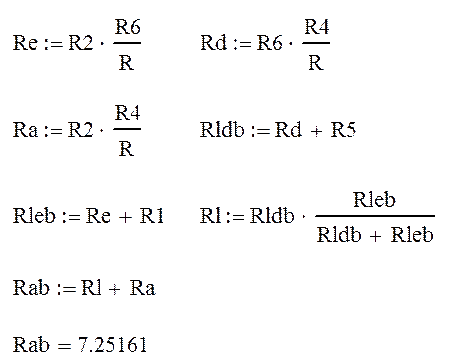
Ux=Uab; Rвх=Rab
Iв3=Ux/(R3+Rвх)=-0,34857 А
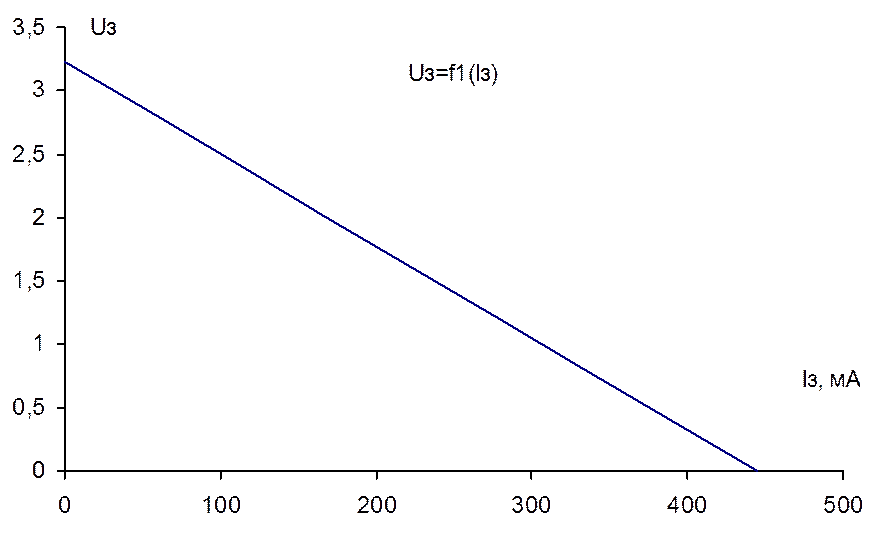
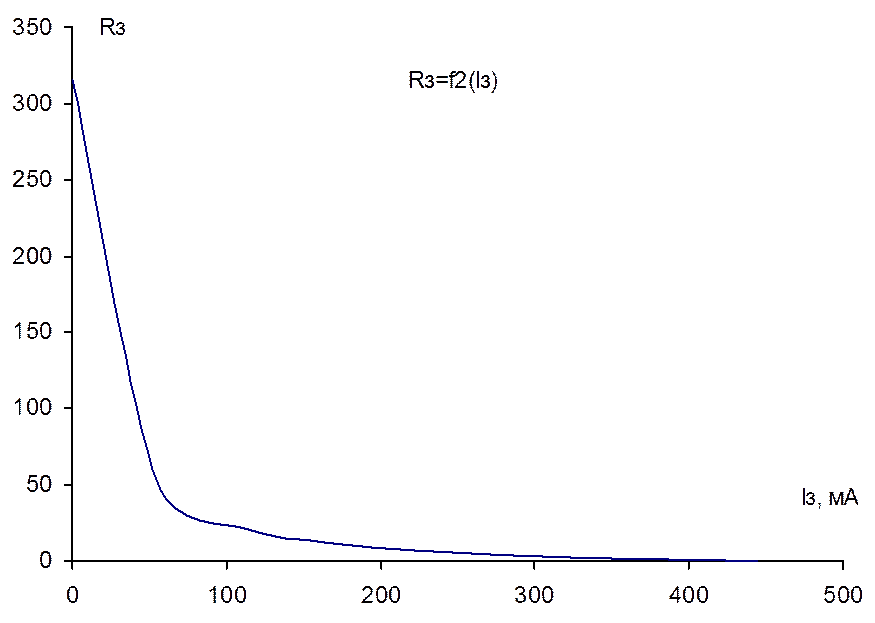
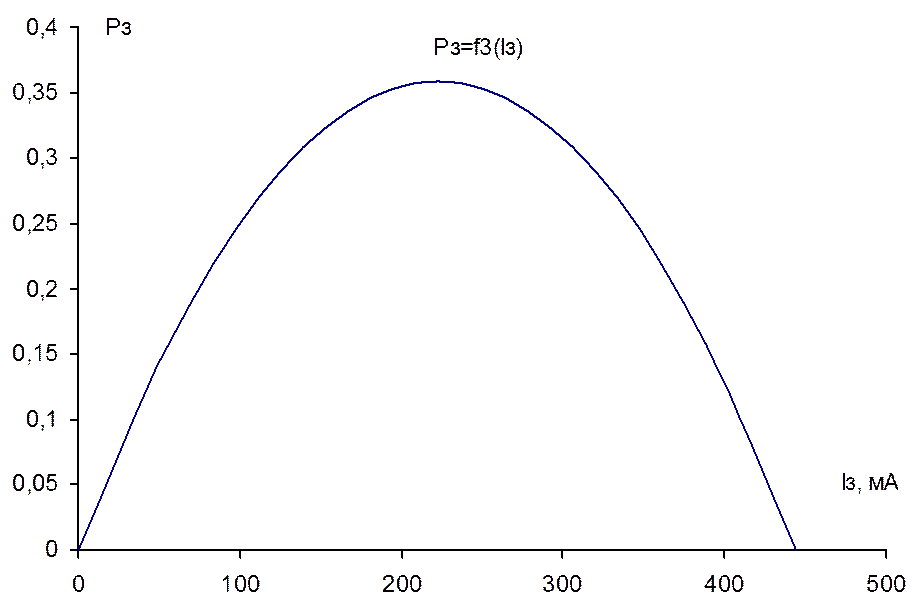
6. Расчет и построение графиков зависимостей U3=f1(I3), P3=f2(I3), R3=f3(I3), при условии, что R3 изменяется от 0 до ∞.
I3кз=Eэ/Rэ=0,4447 А I3кз/2=0,22235 А
U3= Eэ-I3∙Rэ
R3=Eэ/I3-Rэ
P3=I32∙R3
|
I3, мА |
0 |
55,586 |
111,18 |
166,76 |
222,35 |
277,94 |
333,53 |
389,11 |
444,7 |
|
U3, В |
3,2248 |
2,8217 |
2,4186 |
2,0155 |
1,6124 |
1,2093 |
0,8017 |
0,4031 |
9,03∙10-6 |
|
R3, Ом |
∞ |
50,763 |
21,754 |
12,086 |
7,2517 |
4,3509 |
2,4171 |
1,036 |
2,03∙10-6 |
|
Р3, Вт |
0 |
0,1568 |
0,2689 |
0,3361 |
0,3585 |
0,3361 |
0,2689 |
0,1568 |
0 |
Задача 1.2: Расчет линейной магнитной цепи.
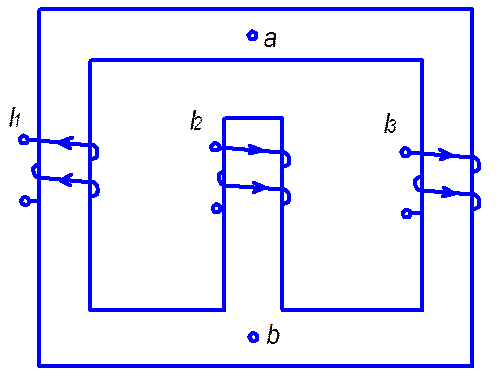 Дано:
Дано:
I1=0,15 А;
I2=0,1 А;
Ф2=15∙10-6 Вб;
ω1=400;
ω2=210;
ω3=150;
|
l1, см |
S1, см2 |
l2, см |
S2, см2 |
l3 , см |
S3, см2 |
lδ, см |
μr |
|
18 |
5 |
8 |
6 |
18 |
5 |
1 |
2∙103 |
1. Составление эквивалентной расчетной схемы замещения линейной магнитной цепи с указанием всех элементов и условно положительных направлений магнитных потоков.
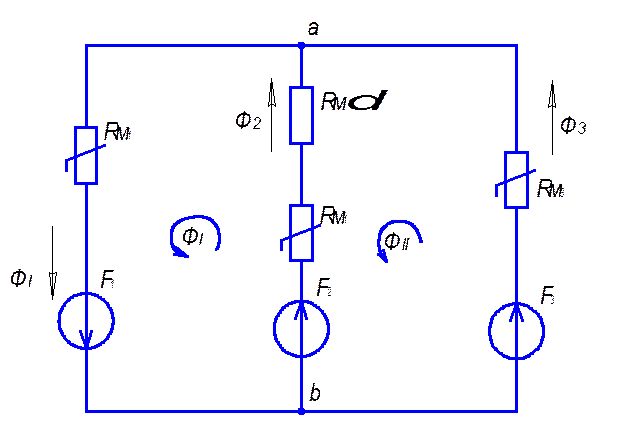 F1=I1∙ω1=60
F1=I1∙ω1=60
F2=I2∙ω2=21
μ= μ0∙ μR=2,512∙10-3
Rmδ=lδ/S2∙μ0=
=1,327∙106 Гн-1
Rm2=(l2-lδ)/S2∙ μ=
=5,242∙104 Гн-1
Rm1=Rm3=l1/S1∙ μ=
=1,433∙105
2. Определение Ф1, Ф3, I3, путем расчета схемы замещения магнитной цепи и использованием законов и методов расчета линейных магнитных цепей.
МКТ:
![]() ФI∙(Rm1+ Rm2+ Rmδ)- ФII∙( Rm2+ Rmδ)=F1+F2
ФI∙(Rm1+ Rm2+ Rmδ)- ФII∙( Rm2+ Rmδ)=F1+F2
ФII∙(Rm1+ Rm2+ Rmδ)- ФI∙( Rm2+ Rmδ)=F3-F2
ФI= Ф3 Ф2= ФII- ФI= Ф1- Ф3; Ф3= Ф1- Ф2
ФII= Ф1
![]() Ф3∙(Rm1+ Rm2+ Rmδ)- Ф1∙( Rm2+ Rmδ)=F1+F2
Ф3∙(Rm1+ Rm2+ Rmδ)- Ф1∙( Rm2+ Rmδ)=F1+F2
Ф1∙(Rm1+ Rm2+ Rmδ)- Ф3∙( Rm2+ Rmδ)=F3-F2
Ф1=(F1+F2+ Ф2∙(Rm1+ Rm2+ Rmδ))/Rm1=2,159∙10-3 Вб
Ф3= Ф1- Ф2=2,009∙10-3 Вб
F3=F2+Ф1∙(Rm1+ Rm2+ Rmδ)-Ф3∙(Rm2+ Rmδ)=537,311 А
I3=F3/ ω3=3,582 А
3. Определение значений магнитной индукции во всех участках магнитной цепи.
В1=Ф1/S1=4,138 Тл; В2=Ф2/S2=0,25 Тл; В3=Ф3/S3=4,018 Тл;
4. Проверка полученного решения по законам Кирхгофа.
Первый закон Кирхгофа:
а: Ф1=Ф2+Ф3
2,159∙10-3=2,159∙10-3
Второй закон Кирхгофа:
Ф1∙Rm1+ Ф2∙(Rm2+ Rmδ)=F3-F2
516,311=516,311
Ф3∙Rm3-Ф2∙(Rm2+ Rmδ)=F1+F2
81=81
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.