Изучение цепи постоянного тока, состоящей из трёх участков

Министерство высшего образования Российской Федерации

Уральский государственный технический университет – УПИ

филиал г. Краснотурьинска

Кафедра электротехники и электротехнологических систем

Лабораторная работа №1

ЦЕПЬ ПОСТОЯННОГО ТОКА

Студенты                   Боярских А. О.

Бронских О. В.

Колесников П. С.

Группа                        Э-2132

Преподаватель Федотова Л. А.

г. Краснотурьинск

2002

Цель работы:

Проверить принцип наложения и свойство взаимности в цепях постоянного тока, состоящих из участков с постоянными сопротивлениями, в которых зависимость напряжения от тока выражается прямой линией (линейных цепях).

Объект исследования:

В работе исследуется сложная цепь, состоящая из трёх участков, в каждом из которых имеется ЭДС. В цепи измеряются токи всех участков как при действии всех ЭДС, так и при действии каждой из этих ЭДС порознь.

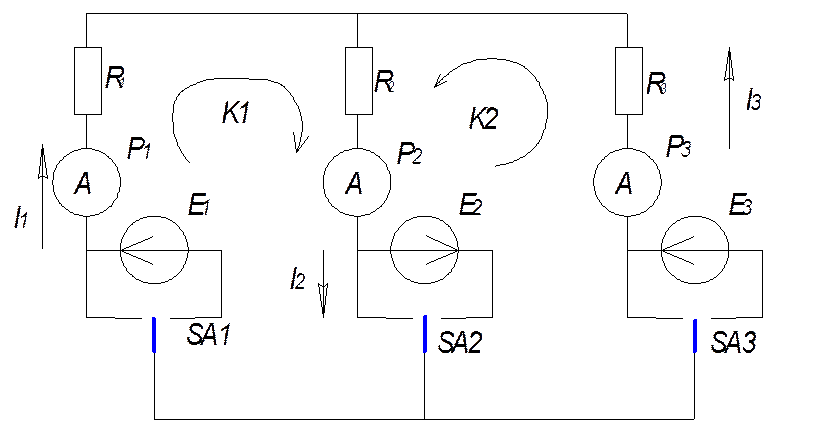
1. Проверка принципа наложения.

Таблица 1. 1.

Токи ветвей	Включены источники
	Е1	Е2	Е3	Е1, Е2, Е3
I1, A	0,5	0,25	-0,25	0,45
I2, A	-0,25	-0,5	-0,25	-0,9
I3, A	-0,25	0,25	0,5	0,45
Алгебр. сумма токов в узле	0	0	0	0

Из таблицы 1.1. видно, что принцип наложения выполняется:

I₁=0,5+0,25-0,25≈0,45 A

I₂=-0,25-0,5-0,25≈-0,9 А

I₃=-0,25+0,25+0,5≈0,45 А

2. Проверка свойства взаимности.

При действии Е₂:

I₁=0,25 A;

                                   I₁=I₂, т. е. свойство взаимности выполняется.

При дествии Е₁:

I₂=-0,25 А; 

Как видно из таблицы 1.1. свойство взаимности выполняется.

3. Определение собственных и взаимных контурных сопротивлений.

Таблица 1.2.

Ветви	Е, В	UR, В	I, A	R, Ом
1	8	5	0,45	11,1
2	8	11	0,9	12,2
3	8	5	0,45	11,1

R=U_R/I

R₁=5/0,45=11,1 Ом                               R₃=5/0,45=11,1 Ом

R₂=11/0,9=12,2 Ом

Нахождение собственных и взаимных контурных сопротивлений по измеренным сопротивлениям ветвей (табл. 1.2.):

R_{I I}=R₁+R₂=23,3 Ом

R_{II II}=R₃+R₂=23,3 Ом

R_{I II}=R_{II I}=R₂=12,2 Ом

Проверка контурных уравнений:

I_I∙R_{I I}+I_II∙R_{I II}=E_I

I_II∙R_{II II}+I_I∙R_{II I}=E_II

I_I=I₁=0,45 A             E_I=E₁+E₂=16 B              

I_II=I₃=0,45 A            E_II=E₃+E₂=16 B

15,975=16

15,975=16

4. Определение собственных и взаимных проводимостей.

4.1. Определение собственных и взаимных проводимостей (по данным, занесенным в табл 1.1.):

Е₂=0, Е₃=0, тогда:

G_{I I}=I_I/E_I=0,5/8=0,0625 Cм

Е₁=0, Е₂=0, тогда:

G_{II II}=I_II­/E­_II=0,5/8=0,0625 См

Е₁=0, E₂=0, тогда:

G_{I II}=I­_I/E_II=-0,25/8=-0,03125 См

E₂=0, E₃=0, тогда:

G_{II I}=I_II/E_I=-0,25/8=-0,03125 См

Проверка  полученных результатов:

I_I=G_{I I}∙E_I+G_{I II}∙E_II               0,5=0,0625∙16-0,03125∙16                  0,5=0,5

I_II=G_{II I}∙E_I+G_{II II}∙E_II                  0,5=-0,03125∙16+0,0625∙16                0,5=0,5

4.2. Вычисление собственных и взаимных проводимостей по найденным контурным сопротивлениям (п. 3) и сравнение их с ранее определенными проводимостями в п. 4.1.

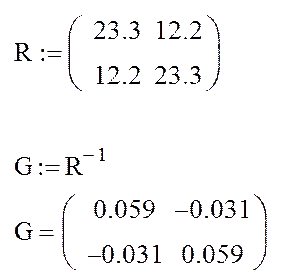
G_{I I}=0,059 Cм

G_{II II}=0,059 Cм

G_{I II}=G_{II I}=-0,031 См

С учетом погрешностей измерительных приборов можно сказать, что данные результаты равны ранее определенным проводимостям в пункте 4.1.

5. Проверка метода эквивалентного генератора.

Для первой ветви:

U_X=8 B

R_BX=R₂∙R₃/( R₂+R₃)=5,82 Ом

I₁=U_X/(R_BX+R₁)=0,47 А

Вывод: в результате лабораторной работы №1 мы проверили принцип наложения и свойство взаимности в цепях постоянного тока, состоящих из участков с постоянными сопротивлениями, в которых зависимость напряжения от тока выражается прямой линией (линейных цепях).