




Министерство образования Российской Федерации
Уральский Государственный Технический Университет
филиал г. Краснотурьинска.
Тема: «Линейные электрические цепи переменного тока в установившихся режимах».
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №2.3
Руководитель Федотова Л. А.
Студент Храмцов А. В.
Группа Э-2132
г. Краснотуринск
2002 г.
Вариант 62.
Задача 2.3: Анализ линейной цепи несинусоидального тока в установившемся режиме.
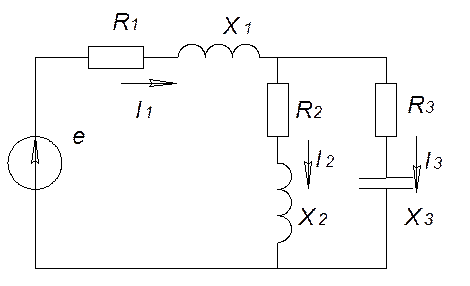
R1=14 Ом; X1=14 Ом;
R2=14 Ом; X2=14 Ом;
R3=14 Ом; X3=14 Ом;
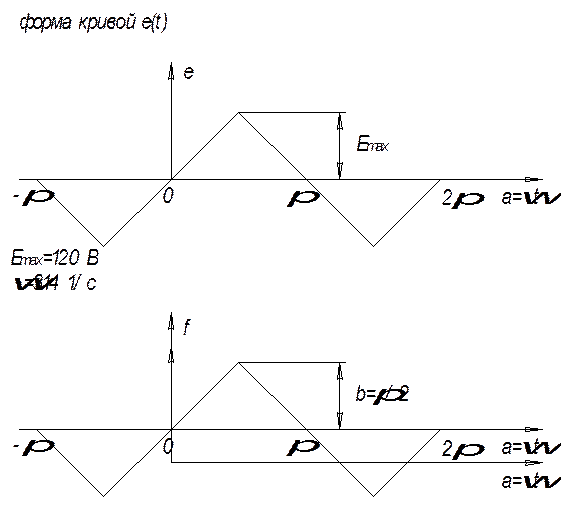
![]() -p-а, -p<a<p/2;
-p-а, -p<a<p/2;
f(a)= a, -p/2<a<p/2;
p-а, p/2<a<p;
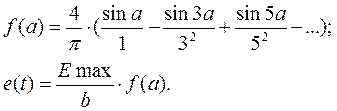
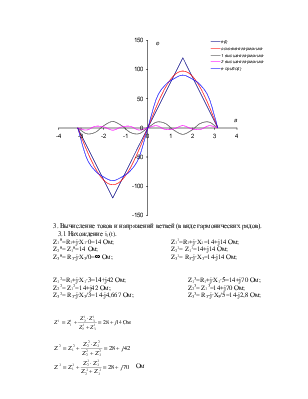
1. Разложение в ряд Фурье заданной несинусоидальной ЭДС e(t).
![]()
2. Построение графиков заданной ЭДС e(t) и приближенной ЭДС еприбл(t), вычисленной в соответствии с рядом Фурье с учётом четырёх его членов: постоянной составляющей, основной гармоники и двух высших гармоник.
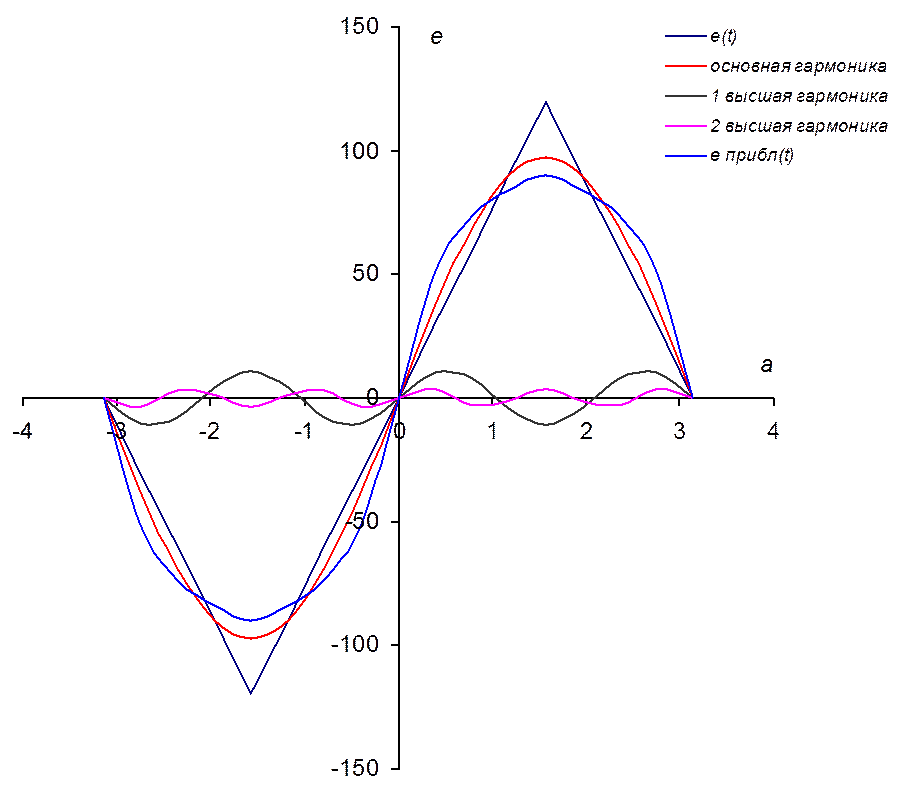
3. Вычисление токов и напряжений ветвей (в виде гармонических рядов).
3.1 Нахождение i1(t).
Z10=R1+j∙X1∙0=14 Ом; Z11=R1+j∙X1=14+j14 Ом;
Z20= Z10=14 Ом; Z21= Z11=14+j14 Ом;
Z30= R3-j∙X3/0=¥ Ом; Z31= R3-j∙X3=14-j14 Ом;
Z12=R1+j∙X1∙3=14+j42 Ом; Z13=R1+j∙X1∙5=14+j70 Ом;
Z22= Z12=14+j42 Ом; Z23= Z13=14+j70 Ом;
Z32= R3-j∙X3/3=14-j4,667 Ом; Z33= R3-j∙X3/5=14-j2,8 Ом;
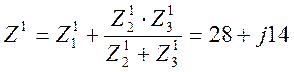 Ом
Ом
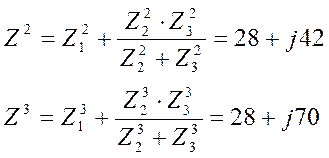
Ом
I01=0 A;
Inm=Enm/Zn
I11m=3,107∙e-j26,565° A;
I12m=0,214∙e-j56,31° A;
I13m=0,052∙e-j68,199° A;
i1(t)=i0+i1+i2+i3=3,107sin(314t-26,565°)+0,214sin(942t-56,31°)+0,052∙ ∙sin(1570t-68,199°)
3.2 Нахождение u1(t).
U01=0 B;
Unm=Inm∙Zn
U11m=61,518∙ej18,435° B;
U12m=9,479∙ej15,255° B;
U13m=3,684∙ej10,491° B;
u1(t)=u0+u1+u2+u3=61,518∙sin(314t+18,435°)+9,479∙sin(942t+15,255°)+ +3,684∙sin(1570t+10,491°)
3.3 Нахождение u23(t).
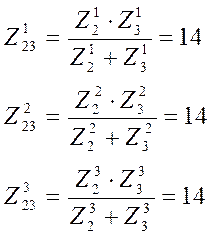
U023=0 B;
Un=Inm∙Zn23
U231m=43,5∙e-j26,565° B;
U232m=2,998∙e-j56,31° B;
U233m=0,723∙e-j68,199° B;
u23(t)=u023+u123+u223+u323=43,5∙sin(314t-26,565°)+2,998∙sin(942t-56,31°)+ +0,723∙sin(1570-68,199°)
3.4 Нахождение i2(t).
I02=0 A;
Inm=U23nm/Zn2
I21m=2,197∙e-j71,565° A;
I22m=0,068∙e-j127,875° A;
I23m=0,01∙e-j146,889° A;
i2(t)=i20+i21+i22+i23=2,197sin(314t-71,565)+0,068sin(942t-127,875°)+ +0,01∙sin(1570t-146,889°)
3.5 Нахождение i3(t).
I03=0 A;
Inm=U23nm/Zn2
I31m=2,197∙ej18,435° A;
I32m=0,203∙e-j37,875° A;
I33m=0,051∙e-j56,889° A;
i3(t)=i30+i31+i32+i33=2,197sin(314t+18,435)+0,203sin(942t-37,875°)+ +0,051∙sin(1570t-56,889°)
4. Вычисление действующих значений токов и напряжений ветвей.
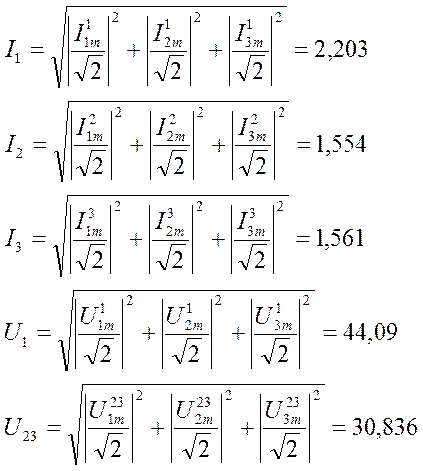
5. Проверка баланса мощностей по активной ее составляющей.
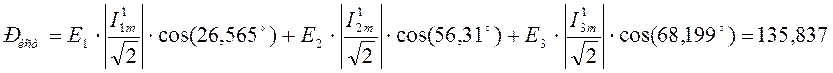 Вт
Вт
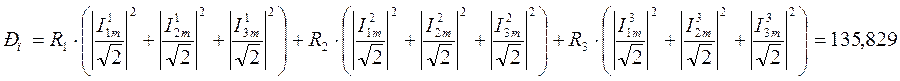 Вт
Вт6. На примере рассматриваемой цепи, исключив из кривой ЭДС постоянную составляющую, показать, что наличие в кривой ЭДС высших гармоник уменьшает коэффициент мощности цепи l по сравнению с коэффициентом мощности cosj этой же цепи при чисто синусоидальной ЭДС основной частоты.
l=P/S=P/(E∙I)
P=P1+P2+P3=135,829 Вт
I=I1=2,203 А
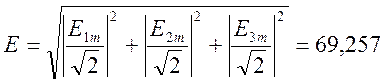 В
В
l=0,8291
cosj=cos(26,565°)=0,8444
cosj>l
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.