







Смысл – там, где змеи интегралы
Меж цифр и букв, меж d и f!
В. Брюсов
ПЛАН
1. Введение.
2. Числа. Действия с числами.
3. Проценты. Задачи на процентный прирост.
4. Действия с приближенными числами.
5. Заключение.
В жизни мы неоднократно встречаемся с различными проявлениями одного из основных законов философии, утверждающего, что движущей силой развития является закон единства и борьбы противоположностей. Верх и низ, впереди и сзади, направо и налево – таковы проявления этого закона в положениях. Построение и разрушение, победа и поражение, эмиграция и иммиграция, отдаление и приближение – это единство и борьба противоположностей в действиях. Субсидирование и изъятие средств, приумножение капитала и банкротство – такого рода явления наблюдаются в экономике. В математике у этого закона своя специфика. О взаимно обратных операциях подробно говорилось уже в школе, таковы сложение и вычитание, умножение и деление, возведение в степень и извлечение корня.
Важнейшей операцией математического анализа является дифференцирование, которое на заданной функции определяет новую функцию – её производную. В свете сказанного вполне естественно поставить вопрос об обратной операции для дифференцирования, которая по заданной производной восстанавливала бы исходную функцию. Интегрирование – так называется эта операция – наряду с дифференцированием является важнейшей составляющей высшей математики, в той или иной форме встречается во всех областях знаний, использующих математические средства для решения своих конкретных задач. Глубинный смысл этого понятия раскрывается в латинской первооснове слова интегрирование – что значит объединение, собирание воедино, в противоположность дифференцированию, которое означает – разделение, разобщение. Слегка перефразируя Библию, скажем так: всему своё время – время разбрасывать камни (дифференцировать) и время собирать камни (интегрировать).
Итак, наступило время интегрировать.
Определение. Функция F(x) называется первообразной (первообразной функцией) для функции f(x) на некотором интервале, если для всех x из этого интервала выполняется равенство:
![]() .
(1.1)
.
(1.1)
Например, функция ![]() является
первообразной для функции
является
первообразной для функции ![]() на бесконечном
интервале (–¥;+¥), так как при любых x выполняется
равенство
на бесконечном
интервале (–¥;+¥), так как при любых x выполняется
равенство ![]() .
.
Функция ![]() является
первообразной для функции
является
первообразной для функции ![]() на интервале
(0;+¥), так как в каждой точке этого интервала выполняется
равенство
на интервале
(0;+¥), так как в каждой точке этого интервала выполняется
равенство ![]() .
.
Функция ![]() первообразная
для функции
первообразная
для функции ![]() на всей числовой прямой, так как в
каждой точке этого интервала выполняется равенство
на всей числовой прямой, так как в
каждой точке этого интервала выполняется равенство ![]() .
.
Легко заметить, что если для данной функции f(x) существует первообразная, то эта первообразная не является единственной. Так, если F(x) есть первообразная для функции f(x), то и функция F(x)+C, где C – произвольная постоянная, также будет первообразной для функции f(x), т.к.
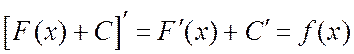 .
.
Отсюда следует, что если функция f(x) имеет хотя бы одну первообразную, то она будет иметь бесконечно много первообразных. Задача интегрирования заключается в том, чтобы для заданной функции найти все ее первообразные. При решении этой задачи основную роль играет следующая теорема.
Теорема 1. Если две различные функции F1(x) и F2(x) являются первообразными для одной и той же функции f(x) на некотором промежутке, то разность между ними равна постоянной величине.
Действительно, по условию
![]() и
и ![]() .
.
Следовательно
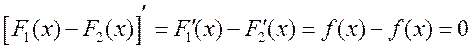 .
.
Из курса дифференциального исчисления известно, что если производная какой-либо функции на некотором промежутке равна нулю, то эта функция является постоянной величиной на всём этом промежутке. Тогда
F1(x) – F2(x) = C,
что и требовалось доказать.
Из приведенной теоремы следует, что все первообразные для одной и той же функции отличаются друг от друга только на постоянную величину. Это означает, например, что по скорости и промежутку времени можно определить величину пройденного точкой пути, однако нельзя определить ее положение.
Определение. Множество всех первообразных для некоторой функции f(x) называется неопределенным интегралом и обозначается символом
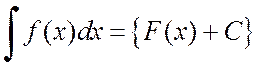 .
(1.2)
.
(1.2)
Символ ò называют знаком интеграла, произведение f(x)dx – подынтегральным выражением, а саму функцию f(x) – подынтегральной функцией.
Следует помнить, что любое равенство, которое содержит неопределенный интеграл, есть равенство между множествами. Однако, чтобы не загромождать формулы, фигурные скобки, обозначающие множество, обычно опускают.
Например,
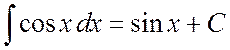 ,
,
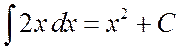 ,
,
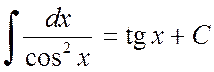 .
.
Далее, естественно, возникает вопрос: для каких функций существуют первообразные, а значит и неопределенные интегралы. Здесь только отметим без обоснования, что если функция f(x) непрерывна на некотором интервале, то для этой функции существуют первообразные F(x). Функции, для которых существую первообразные, называются интегрируемыми. Таким образом, любая непрерывная функция интегрируема, однако не всякая интегрируемая функция непрерывна.
Трудность операции интегрирования состоит в том, что для нее нет универсального правила нахождения первообразных, в отличие от операции дифференцирования. В этом смысле задача интегрирования функций является более творческой и содержательной по сравнению с задачей дифференцирования функций, а потому более сложной (ломать – не строить!). Искусство интегрирования требует определенных навыков, не лишней может оказаться и некоторая изобретательность. Для успеха необходимы не только знания, но и развивающий вкус и воображение собственный опыт, приобретаемый лишь большим самостоятельно вычисленных интегралов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.