Отметим, что неопределенный интеграл даже от элементарной функции может не быть элементарной функцией, тогда как операция дифференцирования не выводит нас из класса элементарных функций, т.е. производная любой элементарной функции представляет собой тоже элементарную функцию. Можно доказать, что интегралы от некоторых элементарных функций уже не являются элементарными функциями. Примерами таких интегралов могут служить следующие интегралы:
|
1.
|
2.
|
3.
|
|
4.
|
5.
|
6.
|
Такие интегралы обычно называют «неберущимися». Однако это не означает, что такие интегралы (первообразные) не существуют. Каждый из указанных интегралов представляет собой функцию, которую нельзя выразить при помощи элементарных функций. Более того, указанные функции не только реально существуют, но и играют большую роль в различных приложениях. Так, например, интеграл 1, называемый интегралом Пуассона или интегралом ошибок, широко используется в теории вероятностей и математической статистике.
В дальнейшем мы будем иметь дело только с такими функциями, которые интегрируются в элементарных функциях, т.е. их первообразные есть элементарные функции.
Суть различных методов интегрирования состоит в том, чтобы при помощи различных преобразований подынтегрального выражения, используя свойства интегралов, свести исходные интегралы к уже известным интегралам. Набор таких известных интегралов можно получить, если переписать наоборот таблицу производных основных элементарных функций. В результате, можно получить следующую таблицу неопределенных интегралов:
|
1.
|
6.
|
|
2. |
7.
|
|
2а. |
8. |
|
2б. |
9. |
|
2в. |
10. |
|
3. |
11. |
|
4. |
12. |
|
4а. |
13. |
|
5. |
14. |
Сделаем замечания в отношении формул 3, 13 и 14.
Формула 3 справедлива для любых значений ![]() .
В самом деле, если u>0, то
.
В самом деле, если u>0, то ![]() , если u<0,
то
, если u<0,
то ![]() . Формулы 13 и 14 занимают
исключительное положение в таблице, ибо эти формулы не имеют аналогов в таблице
производных. Однако в справедливости этих равенств можно убедиться,
продифференцировав их правые части.
. Формулы 13 и 14 занимают
исключительное положение в таблице, ибо эти формулы не имеют аналогов в таблице
производных. Однако в справедливости этих равенств можно убедиться,
продифференцировав их правые части.
Приведенные здесь интегралы называются табличными. В справедливости приведенных равенств можно убедиться при помощи дифференцирования этих равенств. В дальнейшем, мы будем пытаться свести любой интеграл к табличному. Однако для этого нужно знать свойства неопределенных интегралов, вытекающие непосредственно из определения первообразной.
Свойство 1. 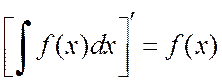 .
.
Свойство 2. 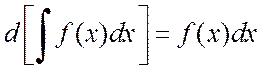 .
.
Свойство 3. 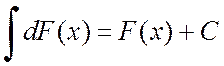 .
.
Эти свойства непосредственно вытекают из определения производной. Действительно
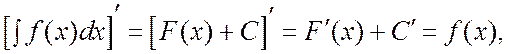
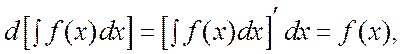
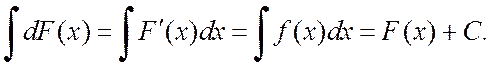
Из данных свойств следует, что интегрирование и дифференцирование – взаимно обратные операции.
Следующие два свойства обычно называют линейными свойствами интеграла:
Свойство 4. 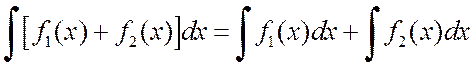 .
.
Свойство 5. 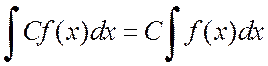 , где C
= const.
, где C
= const.
Чтобы доказать эти свойства, нужно взять производную от обеих частей данных равенств и сравнить их. Подчеркнем, что рассматриваемые равенства имеют условный характер: их следует понимать как равенства двух множеств. Это означает, что данные равенства справедливы с точностью до произвольной постоянной.
Зная свойства интегралов и проводя элементарные преобразования подынтегрального выражения, можно легко свести некоторые интегралы к табличным. Вычисление интегралов, которые легко сводятся к табличным, называют иногда табличным интегрированием. При этом полезно иметь в виду следующее свойство:
Свойство 6. 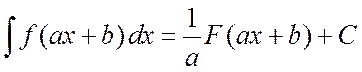 .
.
Чтобы доказать это свойство, нужно продифференцировать обе части данного равенства. Действительно, получаем
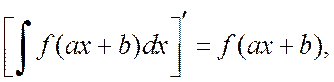
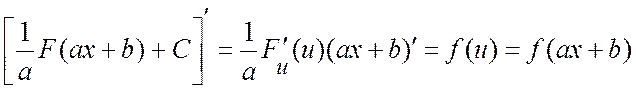 .
.
Примеры 1.1. Вычислить интегралы
а) 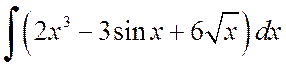 , б)
, б) 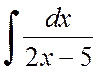 , в)
, в) 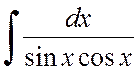 .
.
Решение. а) Используя свойства 4 и 5, получим
![]()
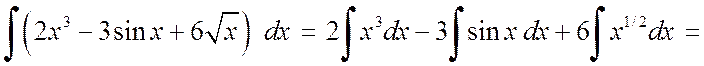
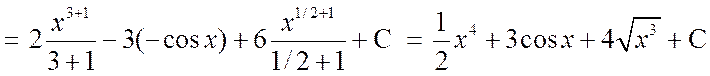 .
.
б) Воспользуемся свойством 6, где a=2, и табличным интегралом 3. Тогда получим
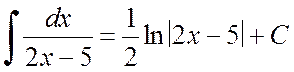 .
.
в) Предварительно произведем тригонометрические преобразования подынтегрального выражения, воспользовавшись тождеством: cos2x + sin2x = 1. В результате получим
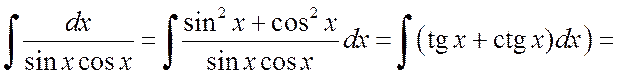
![]() .
.
Рассмотрим теперь интегралы, которые сводятся к табличным интегралам вида:
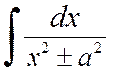 ,
, 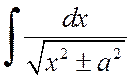 или
или 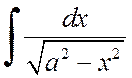 .
.
Обычно к таким интегралам сводятся выражения, которые содержат квадратный трехчлен:
ax2+bx+c.
Подобные интегралы обычно решают методом выделения полного квадрата. Записывая квадратный трехчлен в виде:
a(t2 ± k2),
где
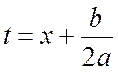 ,
, 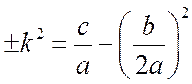 ,
можно прийти к табличным интегралам, рассматриваемого типа.
,
можно прийти к табличным интегралам, рассматриваемого типа.
Примеры 1.2. Вычислить интегралы
а) 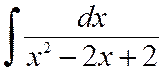 , б)
, б) 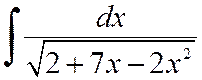 .
.
Решение. а) Выделим из квадратного трехчлена полный квадрат:
x2–2x+2 = (x2–2x+1)+1 = (x–1)2+1.
Тогда
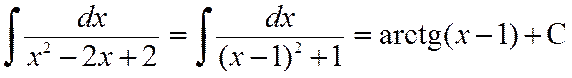 .
.
б) Выделим полный квадрат из квадратного трехчлена

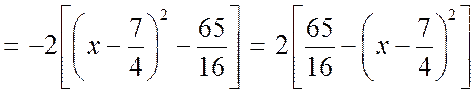 .
.
Тогда
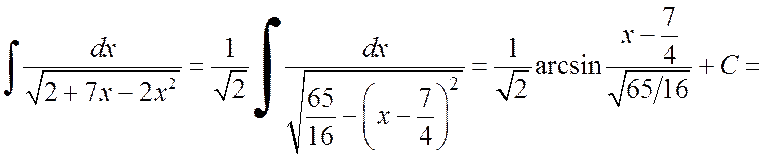
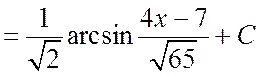 .
.
1. Дайте определение первообразной.
2. Сколько существует первообразных для одной и той же функции? Как они отличаются дуг от друга
3. Что такое неопределенный интеграл?
4. Как составляется таблица интегралов? Запишите по памяти таблицу интегралов.
5. Какие интегралы называются неберущимися?
6. Для всех ли функций существуют первообразные? Как такие функции называются?
7. Перечислите свойства интегралов.
1. Вычислить интегралы
|
а) |
б) |
в) |
г) |
д) |
2. Вычислить интегралы
|
а) |
б) |
в) |
3. Вычислить интегралы
|
а) |
б) |
в) |
4. Вычислить интегралы
|
а) |
б) |
в) |
д) |
5. Вычислить интегралы
|
а) |
б) |
в) |
д) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.