Первичная обработка наблюдений двух измеримых признаков исследуемого объекта, страница 6

·  в ячейках H3:H31 представлены значения произведения  х₂y;

·  в ячейках D32,E32,F32,G32,H32 представлена сумма соответствующих значений, которую высчитываем с помощью клавиши “ автосумма “ на понели инструментов, предварительно выделив соответствующий массив ячеек.

3. 

Высчитав необходимые суммы коэффициентов и произведений, вводим их в отдельные массивы ячеек, т.е. представляем их в виде матриц для удобства расчетов. Отобразим полученные матрицы  окном  Excel, обозначив как рисунок 1.

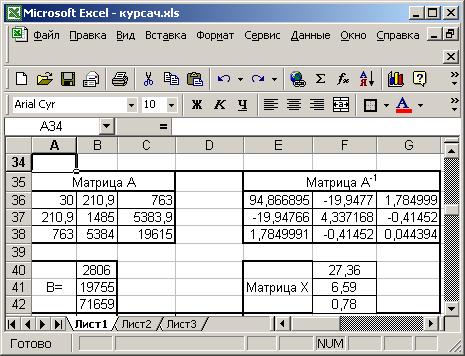Рис.1 Вид окна Excel с отображаемыми данными

Комментарии к таблице 5:

·  в ячейки А36:С38 введены соответствующие значения:

1) ячейка А36- n –число наблюдений;

2)в ячейки В36,С36,А37:С38-соответствующие суммы Σх₁, Σх₂, Σх₁, Σх₁², Σх₁х₂, Σх₂, Σх₁х₂, Σх₂².

·  в ячейках Е36:G38 представлены данные матрицы А^-1, являющейся обратной матрице А. Вычисляют А^-1 с помощью “мастера функций” , а именно функции МОБР, предварительно выделив интервал ячеек, который необходим для отображения матрицы А^-1и после введения определенного интервала ячеек, одновременно нажимаем клавиши Ctrl+Shift+Enter.

·  в ячейках В40:В42 представлены соответствующие значения: Σy, Σх₁y, Σх₂y, в виде матрицы В.

·  в ячейках F40:F42 представлены итоговые результаты в виде матрицы Х. Эти результаты получены умножением матрицы А^-1на В. В среде Excel умножение двух матриц выполняется с помощью "мастера функций” , а именно функции МУМНОЖ .

Таким образом, нашли неизвестные коэффициенты a₀,a₁,a₂ , следовательно, можно составить уравнение регрессии , оно будет выглядеть так

y(х₁, x₂) = 27.36+ 6.59 x₁+ 0.78 x₂.

4.  Следующим шагом  является нахождение теоретических значений отклика (у_Т) по полученному уравнению регрессии и вычислению разности между экспериментальными значениями отклика и значениями  у_Т.

Таблица 6

Продолжение

Комментарии к таблице 6:

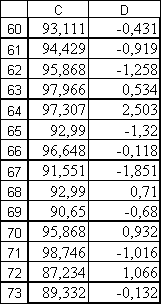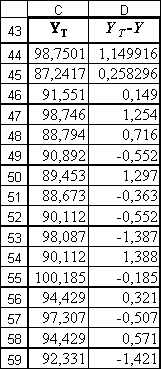
·  в ячейках С43:С73 представлены теоретические данные отклика (у_Т), вычисленные по уравнению регрессии, полученному предыдущим третьим  шагом 

y(х₁, x₂) = 27.36+ 6.59 x₁+ 0.78 x₂.

·  в ячейках D43:D73 представлены результаты вычисления разности у_Т –у.

5)Для построения графика зависимости заданных и найденных (теоретических) значений отклика от номера наблюдения, воспользуемся функцией среды Excel “мастер диаграмм”(порядок выполнение в комментариях). Графики представлены на рисунке1.