Определение 7.4. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний от двух заданных точек, называемых фокусами, есть величина постоянная, равная 2а, при условии, что 2а > 2с, где 2с – расстояние между фокусами.
Фокусы эллипса лежат на оси абсцисс, начало координат
– в середине отрезка между фокусами, их координаты соответственно 
. Они располагаются внутри эллипса.
Уравнение эллипса:
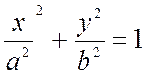, (7.12)
где
(рис.7.9).
Если
центр симметрии эллипса смещен в точку 
),
то уравнение эллипса будет записано так:
.
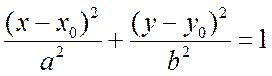(7.13)
Как видно из уравнений эллипса, его график симметричен
относительно обеих осей координат и каждому значению х соответствует два
значения у. Кроме того график пересекает оси координат в точках 
и 
.
Эти точки называют вершинами эллипса. Для удобства его построения строят
основной прямоугольник со сторонами, параллельными осям координат: х = а,
х = –а, у = b, у = –b,
и вписывают в него эллипс.
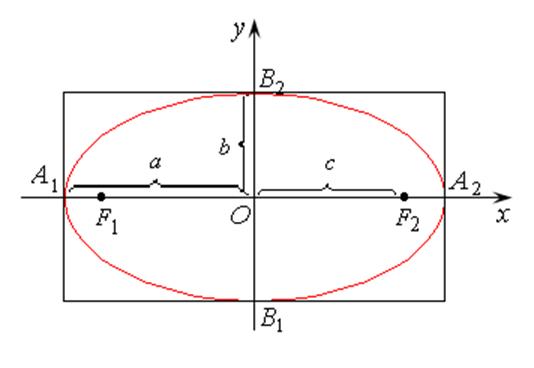
Рис. 7.9
Определение 7.5. Гиперболой называется
геометрическое место точек плоскости, для каждой из которых модуль разности
расстояний до двух заданных, называемых фокусами, есть величина
постоянная, равная 2а, при условии, что 
,
где 2с – расстояние между фокусами.
Фокусы гиперболы располагают
на оси ОХ, которую называют фокальной и действительной
осью, потому что только с ней пересекаются вершины гиперболы в точках . Фокусы гиперболы лежат на более
удаленном расстоянии от начала координат, чем вершины, так как по условию . Пересечения с осью ОУ нет,
поэтому ее называют еще мнимой осью гиперболы.
Уравнение гиперболы:
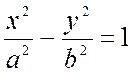, (7.14)
где 
(рис.
7.10).
То же уравнение гиперболы со смещенным центром
симметрии в точке (
запишется в виде:
.
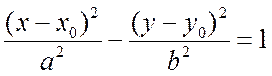(7.15)
Гипербола также симметрична относительно обеих осей
координат. При построении ее графика также строится основной прямоугольник со
сторонами
и 
,
затем проводят его диагонали. Они будут служить асимптотами – прямыми, к
которым стремятся точки графика гиперболы, но не достигают при неограниченном удалении
x от начала координат. Если x
неограниченно удаляется от начала координат, то y тоже будет
уходить в бесконечность. График гиперболы приведен на рис. 7.10. Если фокальной
и действительной осью будет служить ось ОY, то
уравнение такой гиперболы будет записано так:
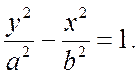
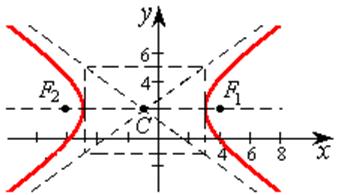
На рис. 7.10 она изображена пунктирной линией.
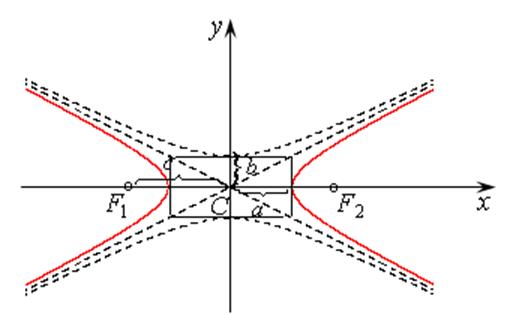
Рис. 7.10
Все перечисленные уравнения носят название канонических уравнений, так как для их вывода использовался один и тот же прием.
Итак, мы рассмотрели четыре кривых второго порядка:
окружность, параболу, эллипс и гиперболу. Возникает вопрос: существуют ли
другие линии, определяемые уравнением второй степени 
?
Чтобы ответить на этот вопрос, приведем примеры.
1) 
.
Этому уравнению удовлетворяет только одна точка на плоскости О(0,0), т.к. сумма
квадратов двух чисел всегда больше нуля.
2) 
.
Это уравнение можно переписать в виде (х – у)(х + у)=0,
и приравнять каждый из сомножителей нулю. Получим две пересекающиеся прямые х
= у и х = –у.
3) х
–
2ху + у = 0. Оно равносильно 
уравнению 
=
0, которое представляет две слившиеся прямые х – у = 0.
4) 
, 
. Каждое из этих уравнений также
представляет пары прямых х = 
, у = 
.
5) 
.
Это уравнение не может определять никакую линию на плоскости, так как сумма
положительных чисел не может быть равно нулю.
Приведенные примеры показывают, что нельзя однозначно ответить на поставленный вопрос. Необходимо подходить к каждому случаю отдельно.
Рассматривая уравнения второго порядка, не содержащие члена с произведением координат, можно привести его к одному из рассмотренных выше видов с помощью выделения полного квадрата по каждой из переменных. Покажем, как это делается, на примере.
Пример 7.7. Привести уравнение к каноническому виду, указать вид кривой.
.
Решение. Представим левую часть в виде суммы квадратов:
(х
– 1 + (у
– 9 – 7 = 0,
или
.
Это уравнение представляет
окружность с центром в точке (–1,–3) и радиусом, равным 
.
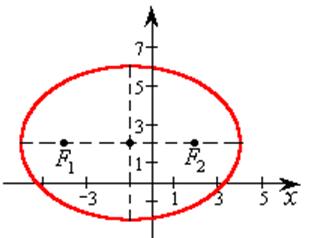
Пример 7.8. Показать, что данное уравнение
16x2 + 25y2 + 32x – 100y – 284 = 0
определяет эллипс, приведя его к каноническому виду. Найти центр эллипса, его полуоси и фокусы. Сделать чертеж
Решение.
Сгруппируем слагаемые, содержащие x и y:
16(x2 + 2x) + 25(y2– 4y) – 284 = 0
После этого выражения в скобках преобразуем таким образом, чтобы можно было воспользоваться формулой полного квадрата, т.е. в каждой скобке добавим и отнимем такое число, чтобы можно было воспользоваться формулой: a2 + 2ab + b2 = (a + b)2:
.
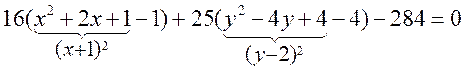Отсюда получаем:
16(x2+1)2 – 16 + 25(y2–2)2 – 100 – 284 = 0,
или
16(x2+1)2 + 25(y2–2)2 = 400.
Разделив это уравнение на 400, получим
.
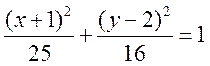Это уравнение – каноническое
уравнение эллипса, центр которого находится в точке С(–1,2). Большая
полуось равна a=4, малая b=3,
фокальное расстояние 
.
Пример 7.9. Показать, что уравнение
9x2 –16y2 + 18x + 64y – 199 = 0
определяет гиперболу, приведя его к каноническому виду. Найти центр гиперболы, ее полуоси, фокусы и уравнения асимптот. Сделать чертеж.
Решение. Дополняя члены, содержащие x и y, до полного квадрата:
9(x2 + 2x) – 16(y2 – 4y) – 199 = 0,
или
9(x + 1)2 – 9 – 16(y – 2)2 + 64 – 199 = 0.
Отсюда получаем каноническое уравнение гиперболы:
.
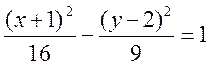Следовательно, центр гиперболы
находится в точке С(–1;2), действительная полуось a=4,
мнимая b=3, фокальное расстояние 
. Уравнения асимптот имеют вид
,
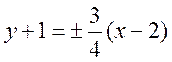или 3x–4y–10 = 0 и 3x+4y–2 = 0.
Построение гиперболы лучше начинать с построения асимптот, а затем уже отмечать вершины, фокусы и другие точки.
На этом мы закончим знакомство с аналитической геометрии, и перейдем к новой теме, которая называется математический анализ. Основным понятием этого раздела высшей математики является понятие функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.