Кстати, последнее неравенство как раз и говорит о непараллельности их нормальных векторов.
Если прямые параллельны, то система решения не имеет. Аналитически это будет выглядеть так:
.
Но если все три дроби равны, то прямые совпадают друг с другом, и поэтому система имеет бесконечное множество решений.
Угол между двумя прямыми можно найти по двум формулам.
Если прямые заданы общими уравнениями, то угол между ними совпадает с углом между их нормальными векторами. Его вычисляют по формуле (6.9) из предыдущей лекции. Для нашего случая она будет иметь вид:
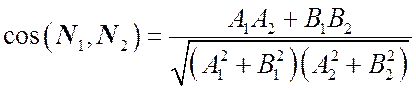. (7.7)
Условие параллельности прямых:
;
Условие перпендикулярности:
.
Если прямые заданы уравнениями с угловыми коэффициентами вида:
и 
,
то тангенс угла между ними определится по формуле:
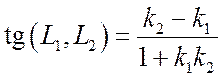. (7.8)
Условие параллельности:
.
Условие перпендикулярности:
.
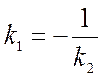Пример 7.4.
Найти точку пересечения прямых 
и 
и угол между ними.
Решение.Найдем точку пересечения прямых, решив систему уравнений методом Крамера:
, 
,
,
, 
.
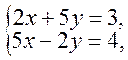
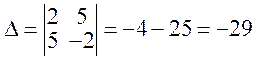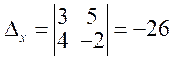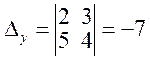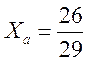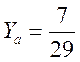Угол между прямыми определим, как угол между их нормальными векторами (2, 5) и (5, –2). По формуле (7.7) имеем:
.
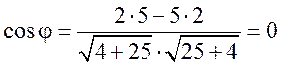О чем говорит этот ответ? Прямые перпендикулярны, т.к.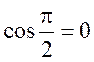 
.
Пример 7.5.
При каком значении параметров a и b прямые 
и 
: а) пересекаются, б)
параллельны, в) совпадают?
Решение.Две прямые пересекаются, если выполняется условие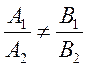 
.
В нашем случае
.
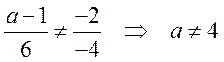Прямые параллельны, если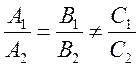 
,
т.е.
.
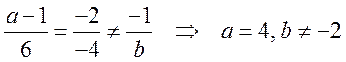И, последнее, две прямые совпадают при условии, что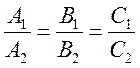 
, т.е. если 
.
Пример
7.6. Дана точка 
и прямая 
. Написать уравнения прямых L1 и L2,
проходящих через точку A, причем 
и 
.
Решение.Сделаем схематичный рисунок.
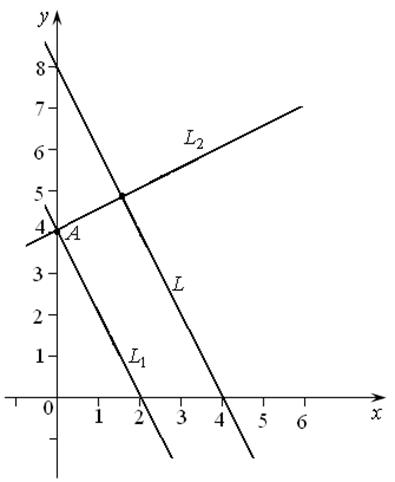
Рис. 7.6
Угловой
коэффициент исходной прямой L равен k = –2. По условию ,
следовательно 
. По формуле (7.4) находим
уравнение прямой L1:
, или 
.
Поскольку 
, то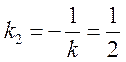 
.
Тогда уравнение прямой L2 будет иметь
вид:
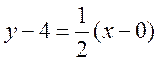, или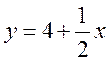 
.
Определение 7.1. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих координат. В общем случае это уравнение имеет вид:
, (7.9)
где все числа А, В, С, и т.д. – действительные числа, и, кроме того, по крайней мере одно из чисел А, В, С – отлично от нуля.
До введения декартовой системы координат все кривые описывались словесно, исходя из геометрических свойств рассматриваемой кривой. Так, определение окружности читалось так:
Определение 7.2. Окружность – это геометрическое место точек на плоскости, равноудаленных от данной точки, называемой центром.
Уравнение окружности, с центром в точке (а, b) и радиусом R в декартовой системе координат, полученное вами в школе, выглядит так:
.
(7.10)
Если раскрыть скобки, то получим уравнение, схожее с уравнением (7.9), в котором отсутствует член, содержащий произведение текущих координат, и коэффициенты при старших степенях равны между собой.
Вывод всех уравнений второго порядка аналогичен выводу уравнений прямой и проходит по тому же алгоритму.
Выведем уравнение параболы, исходя из ее определения.
Определение 7.3. Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой.
Обозначим расстояние от фокуса до директрисы через p. Эта величина называется параметром параболы.
1. Расположим ось абсцисс так, чтобы она проходила через фокус, перпендикулярно директрисе и имела положительное направление от директрисы к фокусу.
2. Начало координат поместим в середину этого
перпендикуляра. Тогда координаты точки будут F(p/2,
0), а уравнение директрисы: 
.
3. Возьмем текущую точку на параболе М(х, у).
4. По определению параболы, расстояние МN от точки М до директрисы равно ее расстоянию МFот фокуса: MF= MN. Как видно из чертежа (рис. 7.7), координаты точки N(–p/2, y). Найдем эти расстояния по формуле расстояния между двумя точками из п. 1 предыдущей лекции.
, 
.
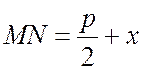Приравняв правые части этих выражений и возведя обе части равенства в квадрат, получим:
,
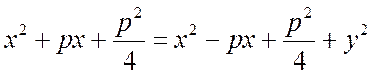или после сокращений
. (7.11)
Уравнение (7.11) называется каноническим уравнением параболы. Ему будут удовлетворять только точки, лежащие на кривой, а остальные – не будут. Исследуем форму ее графика по каноническому уравнению.
Поскольку y входит в четной степени, то
ось ОХ будет являться осью симметрии, т.е. одному значению Х
будет соответствовать два значения Y – положительное и
отрицательное. Т.к. правая часть неотрицательна у
,
то и левая – тоже. Так как р – расстояние между фокусом и директрисой,
всегда больше нуля, то и х
. Если х=0,
то у=0, т.е. парабола проходит через начало координат. При
неограниченном возрастании x абсолютная величина у также будет неограниченно
возрастать.
График параболы, определяемой уравнением (7.11) приведен на рис. 7.7.
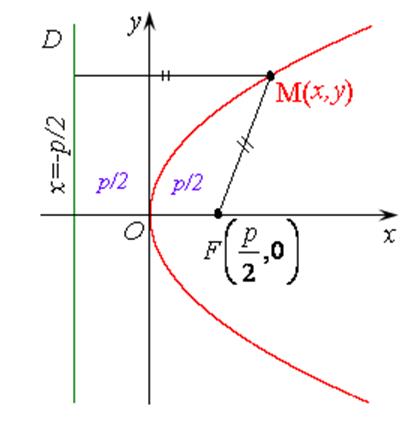
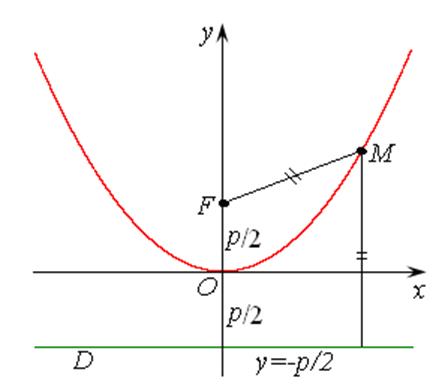
Рис. 7.7 рис. 7.8
Ось симметрии параболы называется фокальной осью, т.к. на ней лежит фокус. Если фокальную ось параболы принять за ось ординат, то ее уравнение примет вид:
.
Ее чертеж показан на рис. 7.8. В этом случае фокус будет находиться в точке F(0, p/2), а уравнение директрисы будет иметь вид у = –р/2.
Таким образом, мы рассмотрели параболу, нашли ее уравнение и показали возможные расположения относительно начала координат.
Если вершина параболы смещена в точку 
, то каноническое уравнение будет
выглядеть так:
.
Выводом остальных кривых второго порядка мы заниматься не будем. Желающие могут найти все выкладки в рекомендуемой литературе.
Ограничимся их определениями и уравнениями.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.