Применение S-функций в Simulink, страница 9

mixed.m моделирует непрерывный интегратор, сопровождаемый дискретной единичной задержкой. В форме блок-схемы Simulink, модель имеет вид.

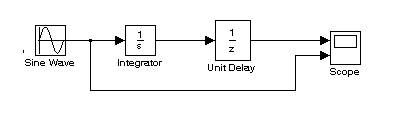
Ниже приведен  код для M-файла S-функции.

function [sys,x0,str,ts] = mixedm(t,x,u,flag)

% пример гибридный системы ,

% состоящей из непрерывного интегратора (1/s) последовательно с

%  задержкой  на один шаг(1/z).

%

% Установить период осуществления выборки и смещений для единичной задержки.

dperiod = 1;

doffset = 0;

switch flag,

  case 0        

    [sys,x0,str,ts] = mdlInitializeSizes(dperiod,doffset);% Инициализация

  case 1

    sys = mdlDerivatives(t,x,u); % Вычислить производные

  case 2

    sys = mdlUpdate(t,x,u,dperiod,doffset); % Модифицировать дисковые состояния

  case 3

    sys = mdlOutputs(t,x,u,doffset,dperiod); % Вычислить выходы

  case {4, 9}

    sys = [];       % Неиспользованные флажки

  otherwise

    error(['unhandled flag = ',num2str(flag)]); % Обработка ошибок

end

% Конец mixedm.

%

%==============================================================

% mdlInitializeSizes

% Возвратить размеры, установить состояния  и  периоды дискретизации .

%==============================================================

function [sys,x0,str,ts] = mdlInitializeSizes(dperiod,doffset)

sizes = simsizes;

sizes.NumContStates  = 1;

sizes.NumDiscStates  = 1;

sizes.NumOutputs     = 1;

sizes.NumInputs      = 1;

sizes.DirFeedthrough = 0;

sizes.NumSampleTimes = 2;

sys = simsizes(sizes);

x0  = ones(2,1);

str = [];

ts  = [0,       0          

       dperiod, doffset]; % Задание времени дискретизации

% Конец mdlInitializeSizes.

%

%==============================================================

% mdlDerivatives

% Вычислить производные для непрерывных состояний.

%==============================================================

%

function sys = mdlDerivatives(t,x,u)

sys = u;

% конец mdlDerivatives.

%

%==============================================================

% mdlUpdate

% Обработать  обновления дискретных состояний, произвести выбор момента

%квантования , и  требований главного шага  квантования.

%==============================================================

%

function sys = mdlUpdate(t,x,u,dperiod,doffset)

% Следующее дискретное  состояние является выходом интегратора.

% Надо возвратить это  дискретное состояние при относительном отклонении

% непрерывного время от значения,   к  ближайшему моменту

%времени кратному дискреному шагу,  менее 1e-8,

%иначе возвращаем [], что указывает, что дискретное состояние не должно измениться.

%

if abs(round((t-doffset)/dperiod)-(t-doffset)/dperiod) < 1e-8

  sys = x(1);

% mdlUpdate "запирает" значение  непрерывного состояния x (1),

%таким образом вводя задержку.

else

  sys = [];  % Этот момент - не момент времени выборки, так матрица sys возвратилась

                  % пустой , чтобы указать, что состояния не имеют  изменений

end         

% Конец mdlUpdate.

%

%==============================================================

% mdlOutputs

% Возвратить вектор выхода для S-функции.

%==============================================================

%

function sys = mdlOutputs(t,x,u,doffset,dperiod)

% возвращение выхода  с единичной задержкой, если мы имеем момент времени

% выборки  в пределах допуска 1e-8, иначе возвращаем [], указывающую,