Применение S-функций в Simulink, страница 8

% Эта S-функциЯ осуществлЯет дискретные уравнениЯ в  форме:

%      x(n+1) = Ax(n) + Bu(n)

%      y(n)   = Cx(n) + Du(n)

%

% Генерировать дискретную линейную систему:

A=[-1.3839 -0.5097

    1.0000         0];

B=[-2.5559         0

         0    4.2382];

C=[      0    2.0761

         0    7.7891];

D=[   -0.8141   -2.9334

       1.2426         0];

switch flag,

  case 0

  [sys,x0,str,ts] = mdlInitializeSizes(A,B,C,D);  % ИНИЦИАЛИЗАЦИЯ

  case 2

    sys = mdlUpdate(t,x,u,A,B,C,D);  % МОДИФИЦИРОВАТЬ ДИСКРЕТНЫЕ СОСТОЯНИЯ

  case 3

    sys = mdlOutputs(t,x,u,A,B,C,D);  % ВЫЧИСЛИТЬ ВЫХОДЫ

  case 9  % Неиспользованные флажки

    sys = [];

  otherwise

    error(['unhandled flag = ',num2str(flag)]); % Обработка ошибок

end

% Конец dsfunc.

%==============================================================

% ИнициализациЯ

%==============================================================

function [sys,x0,str,ts] = mdlInitializeSizes(A,B,C,D)

% Вызвать simsizes длЯ структуры размеров, заполнить её, и конвертировать{преобразовать}

 % к массиву размеров.

sizes = simsizes;

sizes.NumContStates  = 0;

sizes.NumDiscStates  = 2;

sizes.NumOutputs     = 2;

sizes.NumInputs      = 2;

sizes.DirFeedthrough = 1; % Матрица D непуста.

sizes.NumSampleTimes = 1;

sys = simsizes(sizes);

x0  = ones(2,1);   % Инициализировать дискретные состоЯниЯ.

str = [];    % ПриравнЯем str  пустой матрице.

ts  = [1 0];     % период дискретизации и смещение

% Конец mdlInitializeSizes.

%==============================================================

% Модифицировать дискретные состоЯниЯ

%==============================================================

function sys = mdlUpdate(t,x,u,A,B,C,D)

sys = A*x + B*u;

% Конец mdlUpdate.

%==============================================================

% Вычислить выходы

%==============================================================

function sys = mdlOutputs(t,x,u,A,B,C,D)

sys = C*x + D*u;

% Конец mdlOutputs.

Вышеприведенный пример соответствует стадиям моделирования, обсужденным ранее . Системные дискретные уравнения состояния имеют форму

x(n+1) = Ax(n) + Bu(n)

y(n)   = Cx(n) + Du(n)

так, чтобы очень общие наборы разностных уравнений могли быть смоделированы, используя dsfunc.m. Это подобно встроенному блоку Discrete State-Space. Вы можете использовать dsfunc.m как отправная точка для моделирования дискретные системы пространства состояний с изменяющимися во времни коэффициентами.

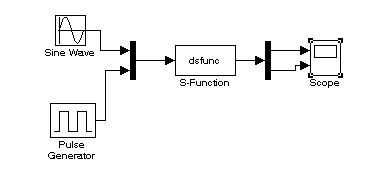
Рис. Модель в Simulink.

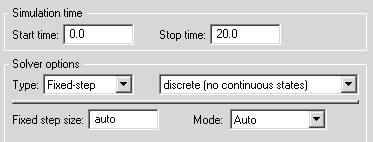
Рис. Параметры моделирования.

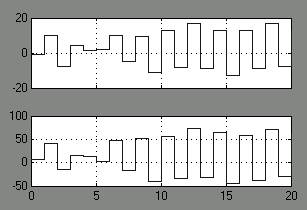
Рис. Результаты моделирования.

Пример -   S-функции гибридных систем.

Simulink включает функцию, названную mixedm.m, который является примером гибридной системы (комбинация непрерывных и дискретных состояний) смоделированный в S-функции. Обработка гибридных систем является довольно прямой; параметр флажка вынуждает вызовы к правильной подпрограмме S-функции для непрерывных и дискретных частей системы. Одна тонкость гибридных S-функций - то, что Simulink вызывает mdlUpdate, mdlOutput, и mdlGetTimeOfNextVarHit подпрограммы во все время сэмплирования. Это означает, что в этих подпрограммах Вы должны проверить, чтобы определить, какой момент времени выборки обрабатывается и только исполнять обновления, которые соответствуют тому моменту времени выборки.