Применение S-функций в Simulink, страница 7

end

% Конец csfunc.

%==============================================================

% mdlInitializeSizes

% Возвратить размеры, задать состоЯниЯ, и указать параметры времени квантованиЯ  длЯ

% S-функции.

%==============================================================

%

function [sys,x0,str,ts] = mdlInitializeSizes(A,B,C,D)

%

% Вызвать simsizes длЯ структуры размеров, заполнить её и конвертировать{преобразовать} 

% к массиву размеров.

%

sizes = simsizes;

sizes.NumContStates  = 2;

sizes.NumDiscStates  = 0;

sizes.NumOutputs     = 2;

sizes.NumInputs      = 2;

sizes.DirFeedthrough = 1;     % Матрица D непуста.

sizes.NumSampleTimes = 1;

sys = simsizes(sizes);

%

% Инициализировать начальные состоЯниЯ.

%

x0 = zeros(2,1);

%

% str - пустаЯ матрица.

%

str = [];

%

% Инициализировать массив типовых времен; в этом примере времЯ сэмплированиЯ

% непрерывно, так что устанавливают ts в 0 и его смещение к 0.

%

ts = [0 0];

% Конец mdlInitializeSizes.

%

%==============================================================

% mdlDerivatives

% Возвратить производные длЯ непрерывных состоЯний.

%==============================================================

function sys = mdlDerivatives(t,x,u,A,B,C,D)

sys = A*x + B*u;

% Конец mdlDerivatives.

%

%==============================================================

% mdlOutputs

% Возвратить выходы блока .

%==============================================================

%

function sys = mdlOutputs(t,x,u,A,B,C,D)

sys = C*x + D*u;

% Конец mdlOutputs.

Вышеупомянутый пример соответствует стадиям моделирования, обсужденным ранее в этой главе. В отличие от timestwo.m, этот пример вызывает mdlDerivatives, чтобы вычислить производные непрерывных фазовых переменных когда флажок = 1.  Уравнения состояния системны имеют форму

x'= Ax + Bu

y = Cx + Du

так, чтобы разные  наборы непрерывных дифференциальных уравнений могли быть смоделированы, используя csfunc.m. Обратите внимание, что csfunc.m подобен встроенному блоку State-Space. Эта S-функция может использоваться как отправная точка для блока, который моделирует систему пространства состояний с изменяющимися во врени коэффициентами.

Каждый раз, когда mdlDerivatives подпрограмму вызывают, она должно явно установить значение всех производных. Вектор производных  не поддерживает не сохраняет значения от последнего вызова  этой подпрограммы. Память, распределенная вектору производных  изменяется в течение выполнения.

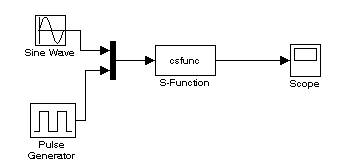
Рис. Модель в Simulink.

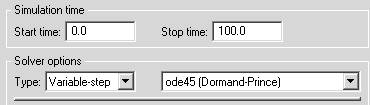
Рис. Параметры моделирования.

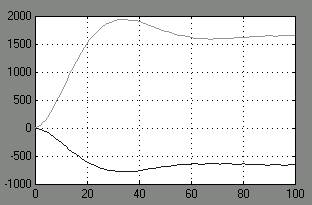
Рис. Результаты моделирования.

Пример -  S-функция с дискретными состояниями

Simulink включает функцию, названную dsfunc.m, которая является примером дискретной системы в пространстве состояний, смоделированная в S-функции. Эта функция подобна  S-функции csfunc.m с непрерывными состояниями. Единственное различие - то, что  вызывают mdlUpdate вместо mdlDerivative. mdlUpdate, модифицирует дискретные состояния когда флажок = 2. Обратите внимание, что из дискретной S-функции с единственным шагом квантования, Simulink вызывает подпрограммы mdlUpdate, mdlOutput, и mdlGetTimeOfNextVarHit (если необходимо)  только на моментах времени выборки. Вот - код для S-функции M-файла.

function [sys,x0,str,ts] = dsfunc(t,x,u,flag)

% S-функциЯ M-файла примера чтобы определЯть дискретную систему.