Решение нелинейных алгебраических уравнений

Лабораторная работа 1. РЕШЕНИЕ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Постановка задачи. Задано нелинейное алгебраическое уравнение f(x)=0. Решением уравнения является значение x*, такое, что f(x*)=0. Решить уравнение приближенным (итерационным) методом ‑ значит построить последовательность {x_n} (n ‑ номер итерации, т.е. приближения к решению), сходящуюся к точному решению уравнения:  Итерационный метод задается рекуррентной формулой, позволяющей определить последующее приближение по известным предыдущим. Итерационный процесс заканчивается, когда   |x_n-x*|<e, где e ‑ точность метода, некоторое наперед заданное число. Перед тем, как начать решение уравнения итерационным методом, необходимо исследовать уравнение на наличие корней и для каждого из корней найти свой интервал изоляции [a,b], содержащего единственный корень уравнения. Условием того, что на отрезке [a,b] существует хотя один корень уравнения является f(a)f(b)<0.

Описание методов решения. Для исследования уравнения используют следующие методы: аналитический, графический и табличный. В настоящей работе функцию будем исследовать с помощью табличного и графического способа. После того, как интервалы изоляции построены, можно решить уравнение с помощью приведенных ниже методов.

1.  Метод деления отрезка пополам. Определяем середину отрезка [a,b]:  и проверяем, какому из двух отрезков (a,c) или (c,b) принадлежит искомый корень, т.е. проверяем: f(a) f(c)<0 либо f(c) f(b)<0. Концы нового отрезка, которому принадлежит корень, обозначаем a, b и повторяем процедуру до тех пор, пока не будет достигнуто условие сходимости итерационного процесса: |b-a|<e.

Вычисления оформляются в виде таблицы

i	a	b	c	f(a)	f(с)
0
1
….

где  a₀ , b₀  - границы интервала изоляции корня;

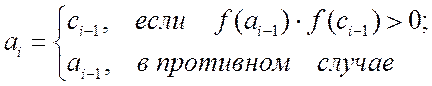
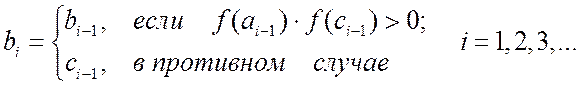
2.  Метод простой итерации. Приведем исходное уравнение к виду, удобному для применения метода простой итерации: x = j(x), где, например, j(x) = x ‑ t f(x). Параметр t подберем таким образом, чтобы выполнялось достаточное условие сходимости метода: 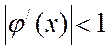для всех xÎ[a,b]. Выберем начальное приближение. Следующие итерации находим по формуле: x_k+1=j(x_k).

Вычисления оформляются в виде таблицы:

i	x
0 1 …	x0 x1 …	….

Условие окончания итерационного процесса .

3.  Метод Ньютона. Выберем начальное приближение x₀Î[a,b]. Следующие итерации определяются по формуле .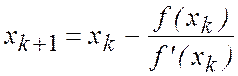

Вычисление оформить в виде таблицы:

i	x	f(x)	f’’(x)
0 1	x0 x1 ...	f(x0) f(x1) …	f ’(x0) f ‘(x1) …	‑ ….

где     

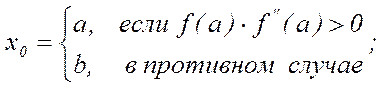
Условие окончания итерационного процесса .

Формулировка задания.

1.  Исследовать функцию f(x) на наличие корней графически. Найти интервалы, на которых существует единственный корень уравнения. Результаты занести в отчет в виде схематических рисунков.

2.  Для каждого интервала изоляции [a,b] с заданной точностью e найти корни уравнения с использованием метода деления отрезка пополам, метода простой итерации, метода Ньютона при e=0.01, e=0.001, e=0.0001

3.  По результатам вычислений составить таблицу:

Метод решения	Значение корня	Количество итераций

4.  В отчет занести: постановку задачи, исследование функции, описание методов решения, результаты расчетов (таблицы), выводы (сравнение результатов, полученных по разным методам и сравнение методов по скорости сходимости).

ВАРИАНТЫ ЗАДАНИЙ

1.  x³  ‑ 0.1x² + 0.4x+ 2=0

2.  x³ ‑ 3x² + 12x=0

3.  x³-3x²+9x-8=0

4.  3x⁴+4x³-12x²+1=0

5.  2x³ ‑ 6x² + 11x-1=0

6.  0.5x³ ‑ 3x² +x+1=0

7.  3x⁴ ‑ 10x³ + 5x-2=0

8.  3x³ ‑ 13x² + 12x-3=0

9.  x³ ‑ 5x² + 12x+1=0

10.  x³ ‑ 2x² + 3x-5=0

11.  x³ ‑ x² + 12x-6=0

12.  x³ ‑ 3x² +x+6=0

13.  x³ ‑ 3x² +2x+2=0

14.  x³ ‑ x² + 2x-1=0

15.  3x³ ‑ 3x² + 12x-8=0

16.  2x³ ‑ x² + 12x-10=0

17.  3x³ ‑ 4x² + 12x-6=0

18.  x³ ‑ 2x² + 4x-3=0

19.  x³ ‑ x² +x-5=0

20.  x³ ‑ 5x² + 4x=0

21.  x³+x²-10x+8=0

22.  x³-7x²-7x+15=0

23.  x³‑ x²-4x+4=0

24.  x³‑ 6x²+3x+10=0

25.  x³‑ 2x²+3x+1=0

26.  x³‑ x²+4x+2=0

27.  x³‑ 6x²+3x-3=0

28.  x³‑ x²+3x-2=0

29.  x³‑ 2x²+3x-3=0

30.  x³‑ 0.1x²+x+2=0