Решить задачу линейного программирования симплексным методом.
Найти наибольшее значение
функции f(x) = 3x![]() + 2x
+ 2x![]() при ограничениях:
при ограничениях: 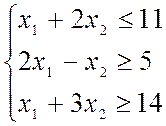
x![]() ≥0, x
≥0, x![]() ≥ 0
≥ 0
Приведём эту задачу к
каноническому виду, введя дополнительные переменные ![]() ,
, ![]() и
и ![]() со
знаком „+ ” для ограничения „≤” и со знаком „-” для ограничения „≥”.
со
знаком „+ ” для ограничения „≤” и со знаком „-” для ограничения „≥”.
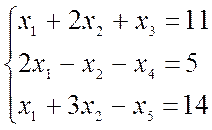
Предварительный анализ
показал, что в базис выводится только x![]() , а при выводе других переменных
значения свободных членов становятся отрицательными, что не допускается. Тогда
для 2-го и 3-го уравнений введём искусственные переменные y
, а при выводе других переменных
значения свободных членов становятся отрицательными, что не допускается. Тогда
для 2-го и 3-го уравнений введём искусственные переменные y![]() и y
и y![]() , которые в дальнейшем будем
использовать как базисные переменные. С этой целью введём эти переменные и в
целевую функцию:
, которые в дальнейшем будем
использовать как базисные переменные. С этой целью введём эти переменные и в
целевую функцию:
max f(![]() ) = 3x
) = 3x![]() +
2x
+
2x![]() + 0x
+ 0x![]() -
M(y
-
M(y![]() + y
+ y![]() ),
),
где М – достаточно большое положительное число
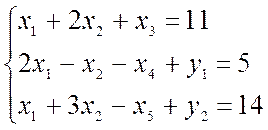
Дальнейшее решение проводим в симплекс-таблицах (табл. 1).
Таблица 1.
|
№ симпл. табл. |
Базис |
Сj |
План В |
3 |
2 |
0 |
0 |
0 |
-М |
-М |
Q |
|
Ci |
А1 |
А2 |
А3 |
А4 |
А5 |
Р1 |
Р2 |
||||
|
0 |
А3 |
0 |
11 |
1 |
2 |
1 |
0 |
0 |
0 |
0 |
11 |
|
←Р1 |
-М |
5 |
2 |
-1 |
0 |
-1 |
0 |
1 |
0 |
5/2 |
|
|
Р2 |
-М |
14 |
1 |
3 |
0 |
0 |
-1 |
0 |
1 |
14 |
|
|
∆j = zj - cj |
Fo=-19М |
-3М-3 |
-2М-2 |
0 |
М |
М |
0 |
0 |
|||
|
I |
А3 |
0 |
17/2 |
0 |
5/2 |
1 |
1/2 |
0 |
0 |
17/5 |
|
|
→А1 |
3 |
5/2 |
1 |
-1/2 |
0 |
-1/2 |
0 |
0 |
|||
|
←Р2 |
-М |
23/2 |
0 |
7/2 |
0 |
1/2 |
-1 |
1 |
23/7 |
||
|
∆j = zj - cj |
Fo=7,5-11,5М |
0 |
-3,5-3,5М |
0 |
-3/2-1/2М |
М |
0 |
||||
|
II |
←А3 |
0 |
2/7 |
0 |
0 |
1 |
1/7 |
5/7 |
2 |
||
|
А1 |
3 |
29/7 |
1 |
0 |
0 |
-3/7 |
-1/7 |
||||
|
→А2 |
2 |
23/7 |
0 |
1 |
0 |
1/7 |
-2/7 |
23 |
|||
|
∆j = zj - cj |
Fo=19 |
0 |
0 |
0 |
-1 |
-1 |
|||||
|
III |
→А4 |
0 |
2 |
0 |
0 |
7 |
1 |
5 |
|||
|
А1 |
3 |
5 |
1 |
0 |
3 |
0 |
2 |
||||
|
А2 |
2 |
3 |
0 |
1 |
-1 |
0 |
-1 |
||||
|
∆j = zj - cj |
Fo=21 |
0 |
0 |
7 |
0 |
4 |
|||||
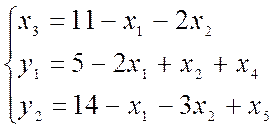
x![]() ,x
,x![]() ,x
,x![]() ,x
,x![]() = 0
= 0
Задача обладает исходным опорным планом: (0; 0; 11; 0; 0; 5; 14)
f(![]() ) = 0∙11 + (-М)∙5 + (-М)∙14 = -19М
) = 0∙11 + (-М)∙5 + (-М)∙14 = -19М
∆![]() =
0∙1+(-М)∙2 + (-М)∙1 – 3 = -3М – 3
=
0∙1+(-М)∙2 + (-М)∙1 – 3 = -3М – 3
∆![]() =
0∙2+(-М)∙(-1) + (-М)∙3 – 2 = -2М - 2
=
0∙2+(-М)∙(-1) + (-М)∙3 – 2 = -2М - 2
∆![]() =
0∙1+(-М)∙0 + (-М)∙0 – 0 = 0
=
0∙1+(-М)∙0 + (-М)∙0 – 0 = 0
∆![]() =
0∙0+(-М)∙(-1) + (-М)∙0 – 0 = М
=
0∙0+(-М)∙(-1) + (-М)∙0 – 0 = М
∆![]() =
0∙0+(-М)∙0 + (-М)∙(-1) – 0 = М
=
0∙0+(-М)∙0 + (-М)∙(-1) – 0 = М
∆![]() =
0∙0+(-М)∙1 + (-М)∙0 – (-М) = 0
=
0∙0+(-М)∙1 + (-М)∙0 – (-М) = 0
∆![]() =
0∙0+(-М)∙0 + (-М)∙1 – (-М) = 0
=
0∙0+(-М)∙0 + (-М)∙1 – (-М) = 0
Q = min(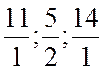 ) = 5/2
) = 5/2
Исходный опорный план не
является оптимальным планом, так как среди оценок ∆![]() имеются
отрицательные оценки. В начальной таблице наименьшее ∆
имеются
отрицательные оценки. В начальной таблице наименьшее ∆![]() соответствует
вектору А
соответствует
вектору А![]() - он вводится в базис, а
искусственный вектор Р
- он вводится в базис, а
искусственный вектор Р![]() из базиса выводится, так
как ему отвечает наименьшее Q =
5/2. Столбец, соответствующий Р
из базиса выводится, так
как ему отвечает наименьшее Q =
5/2. Столбец, соответствующий Р![]() , из дальнейших
симплексных таблиц вычёркивается.
, из дальнейших
симплексных таблиц вычёркивается.
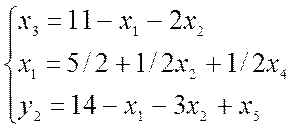 =>
=> 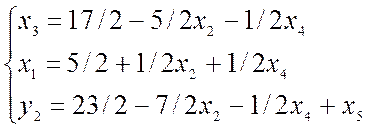
х![]() =
0
=
0
Строка I табл. 1:
опорный план: (5/2; 0; 17/2; 0; 0;23/3)
f(![]() )
= 0∙17/2 + 3∙5/2 + (-М)∙23/2 = 7,5 – 11,5М
)
= 0∙17/2 + 3∙5/2 + (-М)∙23/2 = 7,5 – 11,5М
∆![]() =
0∙0+3∙1 + (-М)∙0 – 3 = 0
=
0∙0+3∙1 + (-М)∙0 – 3 = 0
∆![]() =
0∙5/2+3∙(-1/2) + (-М)∙7/2 – 2 = 3,5 – 3,5М
=
0∙5/2+3∙(-1/2) + (-М)∙7/2 – 2 = 3,5 – 3,5М
∆![]() =
0∙1+3∙0 + (-М)∙0 – 0 = 0
=
0∙1+3∙0 + (-М)∙0 – 0 = 0
∆![]() =
0∙1/2+3∙(-1/2) + (-М)∙1/2 – 0 = - 3/2 – 1/2М
=
0∙1/2+3∙(-1/2) + (-М)∙1/2 – 0 = - 3/2 – 1/2М
∆![]() =
0∙0+3∙0 + (-М)∙(-1) – 0 = М
=
0∙0+3∙0 + (-М)∙(-1) – 0 = М
∆![]() =
0∙0+3∙0 + (-М)∙1 – (-М) = 0
=
0∙0+3∙0 + (-М)∙1 – (-М) = 0
Q = min(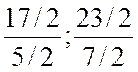 ) = 23/7
) = 23/7
Опорный план строки II табл. 1 не является оптимальным, так
как среди оценок ∆![]() имеются отрицательные
оценки. В строке I наименьшее ∆
имеются отрицательные
оценки. В строке I наименьшее ∆![]() соответствует
вектору А
соответствует
вектору А![]() - он вводится в базис, а
искусственный вектор Р
- он вводится в базис, а
искусственный вектор Р![]() из базиса выводится, так
как ему отвечает наименьшее Q =
23/7. Столбец, соответствующий Р
из базиса выводится, так
как ему отвечает наименьшее Q =
23/7. Столбец, соответствующий Р![]() , из дальнейших
симплексных таблиц вычёркивается.
, из дальнейших
симплексных таблиц вычёркивается.
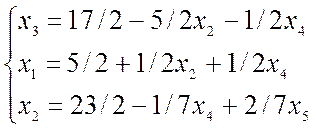 =>
=> 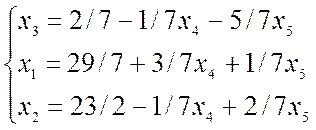
х![]() =
0
=
0
Строка II табл. 1:
опорный план: (29/7; 23/2; 2/7; 0; 0)
f(![]() )
= 0∙2/7 + 3∙29/7 + 2∙23/7 = 133/7 = 19
)
= 0∙2/7 + 3∙29/7 + 2∙23/7 = 133/7 = 19
∆![]() =
0∙0+3∙1 + 2∙0 – 3 = 0
=
0∙0+3∙1 + 2∙0 – 3 = 0
∆![]() =
0∙0+3∙0 + 2∙1 – 2 = 0
=
0∙0+3∙0 + 2∙1 – 2 = 0
∆![]() =
0∙1+3∙0 + 2∙0 – 0 = 0
=
0∙1+3∙0 + 2∙0 – 0 = 0
∆![]() =
0∙1/7+3∙(-3/7) + 2∙1/7 – 0 = - 1
=
0∙1/7+3∙(-3/7) + 2∙1/7 – 0 = - 1
∆![]() =
0∙5/7+3∙(-1/7) + 2∙(-2/7) – 0 = -1
=
0∙5/7+3∙(-1/7) + 2∙(-2/7) – 0 = -1
Q = min(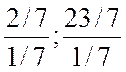 ) = 2
) = 2
Опорный план строки II табл. 1 не является оптимальным, наименьшее
∆![]() соответствует вектору А
соответствует вектору А![]() и А
и А![]() .
Сначала выбираем вектор А
.
Сначала выбираем вектор А![]() - он вводится в
базис, а вектор А
- он вводится в
базис, а вектор А![]() из базиса выводится, так
как ему отвечает наименьшее Q=2.
из базиса выводится, так
как ему отвечает наименьшее Q=2.
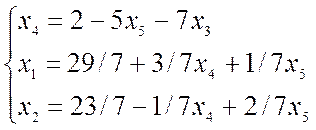 =>
=> 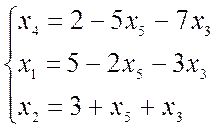
х![]() =
0
=
0
Строка III:
опорный план: (5; 3; 0; 2; 0)
f(![]() )
= 0∙2 + 3∙5 + 2∙3 = 21
)
= 0∙2 + 3∙5 + 2∙3 = 21
∆![]() =
0∙0+3∙1 + 2∙0 – 3 = 0
=
0∙0+3∙1 + 2∙0 – 3 = 0
∆![]() =
0∙0+3∙0 + 2∙1 – 2 = 0
=
0∙0+3∙0 + 2∙1 – 2 = 0
∆![]() =
0∙7+3∙3 + 2∙(-1) – 0 = 7
=
0∙7+3∙3 + 2∙(-1) – 0 = 7
∆![]() =
0∙1+3∙0 + 2∙0 – 0 = 0
=
0∙1+3∙0 + 2∙0 – 0 = 0
∆![]() =
0∙5+3∙2 + 2∙(-1) – 0 = 4
=
0∙5+3∙2 + 2∙(-1) – 0 = 4
Опорный план строки III является оптимальным для исходной
задачи. Для него все ∆![]() ≥ 0, поэтому он является
оптимальным. Таким образом получен оптимальный план исходной задачи (5; 3), и
максимальное значение целевой функции f(
≥ 0, поэтому он является
оптимальным. Таким образом получен оптимальный план исходной задачи (5; 3), и
максимальное значение целевой функции f(![]() ) = 21.
) = 21.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.