Арсеньев Ю.Н.
ТЕМА: СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
Экономико-математическая постановка и формирование моделей обусловливает полезность рекомендаций, связанных с совершенствованием систем массового обслуживания (СМО) в экономической и коммерческой деятельности.
Перспективный класс экономико-математических моделей, с помощью которых можно описывать различные организационно-производственные процессы в любых сферах деятельности общества. К их числу можно отнести системы массового обслуживания (СМО) населения, физических и юридических лиц. Это – разновидности:
- государственных учреждений, вузы, школы, больницы, поликлиники, магазины и т.п.
- банки (коммерческие, инвестиционные, ипотечные, инновационные, сберегательные, трастовые и др.);
- кредитные и страховые организации, налоговые инспекции;
- организации транспорта, связи, торговли и иного обслуживания и др.
Характерной чертой в деятельности этих субъектов рынка является исполнение ими каких-то однотипных задач обслуживания населения, физических и юридических лиц, связанных с потерями рабочего и свободного времени человека и общества.
Для решения задач СМО необходимо:
- проводить наблюдение за процессом обслуживания в системе с целью поиска и выявления существенных связей;
- сформировать проблему, выделить цели, экономические критерии и определить показатели надежности, эффективности и качества работы СМО. Наиболее общим интегральным показателем для СМО выступают затраты деятельности или затраты заявок, имеющие разную по своему физическому содержанию природу.
Повышение эффективности в любой сфере деятельности связано с экономией времени. Экономия времени, равно как и планомерное распределение рабочего времени, по различным отраслям производства - первый экономический закон коллективного производства, проявляющийся во всех сферах социальной деятельности (К. Маркс).
Каждая система массового обслуживания (СМО) может включать в свой состав некоторое число обслуживающих устройств, называемых каналами обслуживания. К их числу можно отнести субъектов, принимающих решения или выполняющих конкретные функциональные задачи или операции - кассиров, операторов, специалистов, менеджеров и др., предназначенных для обслуживания некоторого потока заявок (требований), поступающих на ее вход в случайные моменты времени за любой, обычно случайный, период времени, зависящих от множества самых разнообразных факторов. После обслуживания заявки канал освобождается и готов к выполнению следующей заявки. Случайный характер потока заявок и времени их обслуживания приводит к неравномерности загрузки СМО, как перегрузке каналов обслуживания с образованием очередей заявок, так и недогрузке - с простоем ее каналов. Таким образом, структура любой СМО может иметь (рис. 1.1): входящий поток заявок, очередь, поток не обслуженных (покинувших очередь) заявок, каналы обслуживания и выходной поток обслуженных заявок. Каждая СМО в зависимости от своих параметров — характера потока заявок, числа каналов обслуживания и их производительности и правил организации ее работы обладает определенной эффективностью функционирования (пропускной способностью), позволяющей ей более или менее успешно выполнять предназначенные ей функции. Случайность характера потока заявок и длительности их обслуживания порождает в СМО случайный процесс, для изучения которого необходимо построение и анализ его математической модели.
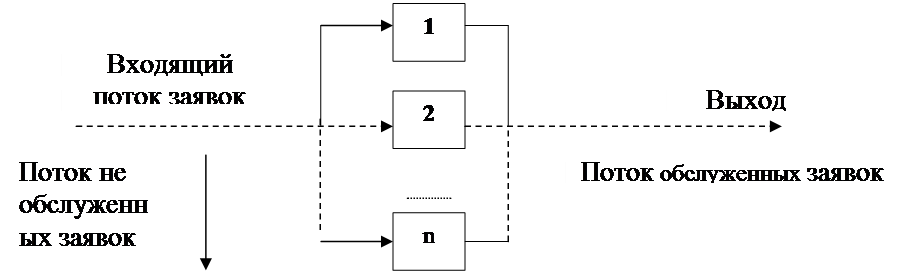 |
Рис. 1.1. Структура системы массового обслуживания
Например, в коммерческой сфере критерий эффективности обусловливается временем и скоростью обращения товаров и интенсивностью поступления денежных средств. Время и скорость обращения товаров характеризуют эффективность использования средств, вложенных в запасы продукции. Оборачиваемость продукции отражает среднюю скорость реализации среднего товарного запаса, а показатели оборачиваемости и уровня запасов взаимосвязаны известными в экономике моделями, учитывающими временные характеристики.
Эффективность работы любого предприятия или организации складывается из совокупности времени выполнения отдельных операций обслуживания. Для населения затраты времени связаны с временем на дорогу, посещения магазина, кафе, сберкассы, больницы, ожидания начала обслуживания, выбора продукции, расчета и др. Исследование структуры затрат времени людей свидетельствуют о нерациональном его расходовании. Вся деятельность человека, в конечном счете, ориентируется на удовлетворение потребностей человека. Поэтому моделирование СМО обычно включает анализ затрат времени по каждой операции обслуживания человека с помощью соответствующих методов, применяющих наиболее общие и известные экономические показатели. К ним обычно относятся: товарооборот, прибыль, издержки обращения, рентабельность и др. Связывание в экономико-математических моделях этой группы показателей с показателями, определяемыми спецификой обслуживающих систем, составляет сущность расчетов, применяемых в теории и системах массового обслуживания.
Например, особенностями показателей СМО с отказами являются: время ожидания (Tоч) заявок в очереди Tоч = 0, так как в таких системах существование очереди невозможно, то длина очереди (Lоч) и вероятность ее образования (Pоч) соответственно равны: Lоч = 0, Lоч = 0. По числу заявок k определяется режим работы системы и ее состояние:
- при k = 0 – простой каналов;
- при 1 < k < n – обслуживание заявок;
- при k > n – обслуживание и отказ.
Показателями СМО с отказами являются:
1) вероятность отказа в обслуживании - Pотк;
2) вероятность обслуживания - Pобс;
3) среднее время простоя канала - t пр;
4) среднее число занятых nз и свободных nсв каналов;
5) среднее время обслуживания - t обс;
6) абсолютная пропускная способность - A.
Для СМО с неограниченным
ожиданием характерно, что вероятность обслуживания заявки Pобс = 1, так как длина очереди (Lоч) и время ожидания начала
обслуживания (Tоч) не ограничены, т.е. Lоч => ![]() и
Tоч =>
и
Tоч => ![]() .
.
В СМО такого рода возможны следующие режимы работы:
- при k = 0 наблюдается простой каналов обслуживания;
- при 1 < k < n – обслуживание;
- при k > n – обслуживание и очередь.
Показателями эффективности СМО с неограниченным ожиданием являются:
1) среднее число заявок в очереди - Lоч,;
2) среднее число заявок в системе - k;
3) среднее время пребывания заявки в системе - Tсмо;
4) абсолютная пропускная способность - A.
Для СМО с ожиданием и с ограничением на длину очереди характерны следующие режимы работы:
- если число заявок в системе k = 0, то наблюдается простой каналов;
- при 1 < k < n – обслуживание;
при n < k < n + m - обслуживание и очередь;
- при k > n + m – обслуживание, очередь и отказ в ожидании обслуживания.
Показателями эффективности таких СМО являются:
1) вероятность отказа в обслуживании - Pотк;
2) вероятность обслуживания - Pобс;
3) среднее число заявок в очереди - Lсмо;
4) среднее время пребывания заявки в системе - Tсмо;
5) абсолютная пропускная способность -A.
Таким образом, перечень характеристик систем массового обслуживания можно представить следующим списком:
1) среднее время обслуживания – t обс ;
2) среднее время ожидания в очереди – T оч;
3) среднее время пребывания в СМО – L смо;
4) количество каналов обслуживания – n;
5) интенсивность входного потока заявок – y;
6) интенсивность обслуживания – u;
7) интенсивность нагрузки – p;
8) коэффициент нагрузки – a;
9) относительная пропускная способность – Q;
10) абсолютная пропускная способность – A;
11) доля времени простоя СМО – Pо;
12) доля обслуженных заявок – Pобс;
15) доля потерянных заявок – P отк;
16) среднее число занятых каналов – n з;
17) среднее число свободных каналов – n св;
18) коэффициент загрузки каналов – Kз;
19) среднее время простоя каналов – t пр.
Следует отметить, что иногда достаточно использовать до десяти основных показателей, чтобы выявить слабые места (обычно - согласованной работы цепочки или совокупностей СМО) и разработать действенные рекомендации по совершенствованию СМО.
В коммерческой деятельности, наряду с перечисленными показателями СМО, следует учитывать еще и их экономические показатели:
1) общие затраты – C;
2) издержки обращения – Cио;
3) издержки потребления – Cип;
4) затраты на обслуживание одной заявки – C1;
5) убытки, связанные с уходом заявки - Cу1;
6) затраты на эксплуатацию канала – Cк;
7) затраты простоя канала – Cпр;
8) капитальные вложения – Cкап;
9) приведенные годовые затраты – Cпр;
10) текущие затраты – Cтек;
11) доход СМО в единицу времени – Д1.
В целом при постановке задачи необходимо раскрыть взаимосвязи показателей СМО, которые по своей базовой принадлежности обычно подразделяют на две группы:
- первая группа показателей определяется издержками обращения Cио, которые зависят от числа занятых обслуживания каналов, затратами на содержание СМО, интенсивностью обслуживания, степенью загрузки и эффективностью использования каналов, пропускной способностью СМО и др.;
- вторая группа показателей определяется издержками собственно заявок Cип, поступающих на обслуживание (они образуют входящий поток, определяют эффективность обслуживания и связаны с такими показателями, как длина очереди, время ожидания обслуживания, вероятность отказа в обслуживании, время пребывания заявки в СМО и др.
Эти две группы показателей противоречивы: улучшение показателей одной группы, например, сокращение длины очереди или времени ожидания в очереди путем увеличения числа каналов обслуживания (врачей, кассиров, рабочих, поваров, учителей, грузчиков и др.) ухудшает показатели другой группы, увеличивая время простоев каналов обслуживания, затраты на их содержание и т.д. Поэтому при формализации задач обслуживания следует реализовать СМО с поиском разумного компромисса между показателями собственно заявок и полноты использования возможностей системы. С этой целью нужен обобщенный интегральный показатель эффективности СМО, включающий одновременно требования и ограничения обеих групп.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.