Применение моделей систем массового обслуживания с отказами на практических примерах анализа эффективности деятельности банковских структур

Арсеньев Ю.Н.

Решение практических задач

 ПРИМЕНЕНИЕ СМО С ОТКАЗАМИ

(на примере решения практических задач)

Поясним применение моделей СМО с отказами на практических примерах анализа эффективности деятельности банковских структур.

Пример 1.1. В филиале банка постоянно работают три (n = 3) оператора. Если клиент заходит в банк, когда все операторы заняты, то он, не ожидая обслуживания, уходит. Среднее число клиентов, обращающихся в банк за 1 ч, составляет 24 чел. Среднее время, затрачиваемое оператором на обслуживание одного клиента, составляет 5 мин. Определить основные характеристики эффективности функционирования данного филиала банка в предельном режиме и найти:

а) вероятность того, что клиент получит отказ р_отк или будет обслужен р_об;

б) среднее число клиентов А, обслуживаемых филиалом в течение 1 ч;

в) среднее число занятых операторов К.

Решение. Данный филиал банка рассмотрим как многоканальную СМО с отказами, когда (n + 1)-й клиент не может ждать обслуживания в очереди, и если все n операторов заняты обслуживанием ранее пришедших клиентов, то данный клиент уходит не обслуженным.

Параметры нашей СМО таковы: n = 3; l = 24 (чел./ч); m = 1/Т_об = 1/5 (чел./мин.) = 12 чел./ч;  r = l/m = 24/12 = 2 эрланга.

Вычислим предельные вероятности состояний системы по формулам (табл. 1.3). Результаты всех вычислений сведем в табл. 1.4.

Итак, вероятность того, что все операторы свободны, составляет:

р₀ = 1/å = 1/6,333 = 0,158.

Значения предельной вероятности р_k определяются как р_k = р_k/р₀.р₀, т.е. путем умножения значений столбца 2 табл. 1.4 на вероятность р₀. Сумма элементов столбца 4 табл. 1.4 соответствует среднему числу занятых каналов К = 1,581.

Вероятность получения клиентом отказа, равна вероятности того, что все три оператора банка заняты, т.е. р₃ = 0,633: 3 = 0,211. Тогда вероятность того, что клиент будет обслужен (или относительную пропускную способность филиала банка), можно определить следующим образом:

Q = 1 - p_отк = 1 - 0,211 = 0,789 = 78,9%.

Таблица 1.4. Результаты расчета параметров трехканальной СМО с отказами

Значения случайной ве- личины k (число заня- тых операторов филиала	Основные вычисления вероятностей отказов при числе занятых каналов k (k = 0, 1, 2, 3)
	рk/р0  = rk/k!	рk	kрk
0 1 2 3 Итого, å	1,000 2,000 2,000 1,333 6,333	0,158 0,316 0,316 0,211 1,001	0 0,316 0,632 0,633 1,581

Следовательно, из 100 обратившихся в банк клиентов 79 чел. в этой СМО обслужат, а 21 чел. получат отказ.

Тогда абсолютная пропускная способность А филиала банка составит:

А = lQ = 24×0,789 = 18,936.

Аналогично пропускную способность А можно подсчитать по формуле: А = mК = 12×1,581 = 18,972 (некоторое расхождение связано с ошибкой округления при вычислении).

Отсюда следует, что решение об организации оптимального числа рабочих мест в филиале банка следует принимать с учетом затрат на содержание каждого оператора и потерь в потенциальном доходе, связанных с долей не обслуженных клиентов.

Пример 1.2. Коммерческий банк решает проблему открытия филиала в населенном пункте N с рассмотрением филиала как многоканальной СМО с отказами, на вход которой поступает простейший поток заявок с интенсивностью l. Производительность каждого канала обслуживания равна m. При этом обслуживание одной заявки (клиента) приносит банку средний доход С₁, создание одного канала обслуживания (оператора) потребует средних издержек С₂, а эксплуатация одного канала в единицу времени - С₃. Найти время t, через которое филиал банка (система) начнет приносить прибыль.

Решение. Пусть случайный процесс, протекающий в СМО, перешел в предельный стационарный режим. СМО начнет приносить доход, если средний доход от обслуживания заявок одним каналом в единицу времени превысит средние издержки эксплуатации одного канала в единицу времени. Согласно задаче это условие можно записать как С₁m > С₃.

Средний доход, приносимый СМО за время t ее эксплуатации в предельном режиме, можно определить следующим образом

АС₁t,

где А — абсолютная пропускная способность СМО (среднее число заявок, обслуживаемых в единицу времени), А_t — среднее число заявок, обслуживаемых за время эксплуатации t.

Согласно формуле (см. табл. 1.3) имеем:

А = mК,

где К - среднее число занятых каналов.

Отсюда средний доход за время t D(t) составит:

D(t) = С₁mКt, (t ³ 0).

Если использовать графическую интерпретацию задачи (рис. 1.4), то график D(t) представляет собой прямую 1, проходящую через начало координат под углом a, причем tga = С₁mК.

Средние издержки за это же время С(t), включающие в себя издержки С₂n, требующиеся на создание n каналов, и средние издержки С₃Кt, требующиеся на эксплуатацию каналов за время t, соответственно составят:

С(t) = С₃Кt + С₂n.

На графике средние издержки С(t) от СМО - это прямая 2, проходящая через точки А (0;С₂n) и В (1; С₃К+ С₂n) под углом b, причем tgb = С₃К.

Так как tg b < tg a и, следовательно, b < a, то прямые 1 и 2 пересекутся.

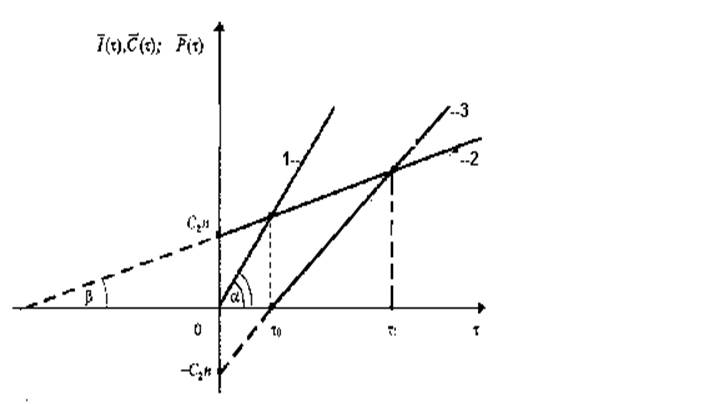Рис. 11.4. Зависимость между доходом (1), средними издержками (2)

и средней прибыльностью (3);  - точка безубыточности.

Абсциссу t₀ точки пересечения Е, в которой средний доход равняется средним издержкам, можно определить из равенства: D(t₀) = C(t₀), т.е.

С₁mКt₀ = С₃mКt₀ + С₂n,

откуда получаем, что

t₀ = С₂n /(С₁m - С₃)К.

Таким образом, точка Е является точкой безубыточности, т.е. через время t₀  СМО начнет приносить среднюю прибыль Р, величина которой равна:

     _         _          _                          _

Р(t) = D(t) —C(t) = (С₁m —С₃)Кt — С₂n.

Если прямая средней прибыли (прямая 3) пересекается с прямой средних издержек (прямой 2), то абсцисса ₁ точки пересечения F определяется как

                  _          _               _             _          _          _            _

Р(t₁) = С(t₁) или С₁mКt₁ - С₃Кt₁ - С₂n  =  С₃Кt₁ + С₂n,

откуда получаем, что                       _

t₁ = 2С₂n /(С₁m — 2С₃)К.

Так как t₁ > 0, то из вышеприведенного соотношения имеем, что С₁m —2С₃ > 0, откуда С₁m > 2С₃. Сравнив ординаты точек Е и F, определим, что в момент времени t₁ средний доход вдвое больше средних издержек.

Если же условие С₁m > 2С₃ не выполняется, т.е. С₁m £ 2С₃, то прямые 2 и 3 в первом квадранте не пересекаются. В частности, при С₁m = 2С₃  эти прямые будут  параллельными.