Нахождение оценки вектора методом наименьших квадратов. Свойства оценок вектора параметров. Гипотезы о значимости оценок

5.1. Введение. Предположения

Рассмотрение простейшей двухфакторной модели, методов исследования, свойств охватывает лишь элементарные экономические ситуации. Более реальными являются эконометрические модели, включающие несколько факторов.

Будем исходить из того, что с целью исследования линейной связи между результирующим фактором Y и объясняющими k-1 факторами X₂, …, X_k было выполнено статистическое наблюдение. В результате наблюдения зарегистрирована выборка объема n, которую представим таблицей вида (табл. 5.1)

Таблица 5.1

Наблюдения факторов

№ п/п	Y	X2	X3	…	Xk
1	Y1	X12	X13	…	X1k
2	Y2	X22	X23	…	X2k
…	…	…	…	…	…
n	Yn	Xn2	Xn3	…	Xnk

Предположим, что существует линейная связь между Y и факторами X₂, …, X_kвида:

,                                               (5.1)

где слагаемое U отражает влияние на других факторов, ошибки измерений, ошибки выбора типа модели. Это предположение назовем гипотезой линейности. Тогда для наблюденных величин (табл. 5.1) можно записать

                               (5.2)

В системе уравнений (5.2) коэффициенты и параметры распределения для случайных величин Ui неизвестны и должны быть оценены. В этом состоит одна из задач, которые необходимо решать.

Систему (5.2) запишем в матричной форме:

,                                                         (5.3)

где

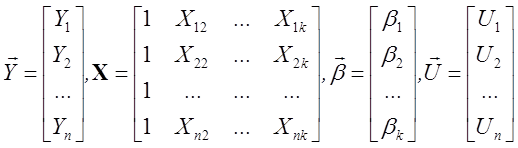 .                           (5.4)

В обозначениях (5.4) матрица наблюдений X содержит столбец, состоящий из единиц. Этот столбец относится к свободному члену .

Для получения оценок вектора примем ряд предположений относительно способа получения наблюдений. В зависимости от сделанных предположений разрабатываются или подбираются методы оценивания.

Основные и наиболее простые гипотезы наряду с гипотезой линейности (5.1) следующие:

;                                                                  (5.5)

;                                                            (5.6)

- матрица фиксированных чисел;                                           (5.7)

                                                            (5.8)

.                                                   (5.9)

Гипотеза (5.5) означает, что  для всех i , т.е. что случайные переменные Ui имеют нулевое математическое ожидание.

Гипотеза (5.6) очень важна в том смысле, что она отражает совокупность свойств ковариационной матрицы In - единичная матрица размерности n. В этой гипотезе выражены свойства, выполнение которых мы требуем. Первое: - это свойство некоррелированности случайных величин ; второе:  для всех i - свойство постоянства дисперсии случайных величин Ui , называемое гомоскедастичностью.

Гипотеза (5.7) является обобщением на случай нескольких факторов аналогичного предположения о постоянстве фактора X в случае линейной двухфакторной модели.

Тем самым оказывается, что у вектора единственным источником возмущений является случайный вектор . В этом случае говорят, что свойства искомых оценок и критериев обусловлены матрицей наблюдений X.

Гипотеза (5.8) характеризует, во-первых, отсутствие строгой линейной зависимости между объясняющими переменными  и, во-вторых, что число наблюдений n больше числа объясняющих переменных k. В соотношении (5.8) обозначение выражает ранг матрицы X.

Принадлежность вектора возмущений  множеству нормально распределенных векторных случайных величин, выраженная в (5.9), фактически объединяет предположения (5.5) и (5.6).

5.2. Нахождение оценки  вектора  методом наименьших квадратов

Обозначим через  - вектор-столбец, оценивающий вектор . Можем записать:

                                                             (5.10)

где через  обозначен вектор-столбец остатков  .

Критерий - сумма квадратов компонент вектора остатков - имеет вид

.                               (5.11)

Для нахождения значения , минимизирующего эту сумму квадратов отклонений, продифференцируем (5.11) по . Приравнивая полученное выражение нулевому вектору, получаем систему нормальных уравнений в векторно-матричной форме (сравни с (3.14)):

.                                                           (5.12)

На основе гипотезы (5.8) получаем основной результат:

.                                                    (5.13)

Оценка  вектора параметров  найдена.

5.3. Свойства оценок вектора параметров  

Подставляя (5.3) в (5.13), можно получить следующее важное представление для оценки :

.                                                  (5.14)

Отсюда сразу следует, что

.                                                           (5.15)

Результат (5.15) означает, что вектор оценок   является несмещенным.

Можно показать, что ковариационная матрица вектора оценок  имеет вид:

.                                (5.16)

Равенство (5.16) означает, что дисперсия компоненты  вектора  может быть оценена путем перемножения i-го элемента главной диагонали матрицы  на дисперсию случайного возмущения . Аналогично ковариация пары оценок  и  определяется умножением (i,j)-го элемента матрицы  на .

Подытоживая рассмотрение свойств оценок  , отметим, что в силу предположения (5.9) элементы вектора  удовлетворяют многомерному нормальному распределению, т.е.

.                                               (5.17)

5.4. Гипотезы о значимости оценок типа

Если дисперсия  возмущений Uизвестна, то факты, представленные соотношениями  (5.13), (5.14), (5.16) могут быть непосредственно использованы для проверки значимости компонент вектора  и построения доверительных интервалов. В случае незнания  можно поступить следующим образом. Так как  и  есть линейные комбинации нормально распределенных случайных величин, то они тоже распределены нормально. Можно показать, что , где  – нулевая матрица из n строк и k столбцов. Последнее означает, что они распределены независимо друг от друга.

Этот результат позволяет использовать t-распределение для проверки гипотез относительно каждого из регрессионных коэффициентов . Величина имеет независимое от  распределение с  степенями свободы. Отсюда по определению t-распределения величина

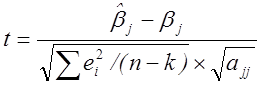                                              (5.18)

удовлетворяет t-распределению с степенями свободы.

Гипотеза о значимости  проверяется следующим образом. В (5.18) подставляем интересующее нас гипотетическое значение  и рассчитываем t. Значение t сравниваем с критическим , соответствующим степеням свободы и  %-му уровню доверия. Если окажется, что выполнено неравенство

,

то гипотеза о значимости  отбрасывается.

Примером проверки отсутствия линейной зависимости Y от X является проверка гипотезы H₀ : .

Соотношение (5.18) дает  %-ный доверительный интервал для  вида

Рассмотрим подход к совместной проверке гипотез относительно нескольких или всех .

Выдвинем нулевую гипотезу

против альтернативной , состоящей в том, что не все  равны нулю. Вектор . Нулевая гипотеза предполагает, что отсутствует влияние всех  факторов  на .