Министерство образования и науки Российской Федерации
Новосибирский государственный технический университет
Кафедра экономической информатики
Лабораторная работа №3
по дисциплине «Прикладные методы оптимизации»
Вариант №2
Факультет Бизнеса
Группа: ФБИ
Студент:
Преподаватель: Кириллов Ю.В.
Новосибирск
2007
Цель работы:
1) понимать смысл, различать, осознанно использовать следующие понятия: математическая модель ЗЦЛП; допустимая область решений ЗЦЛП; правило отсечения в методе Гомори; релаксированная ЗЦЛП, разбиение множества решений релаксированной ЗЦЛП на подмножества решений, дерево решений, рекорд – в методе ветвей и границ для ЗЦЛП; модель динамического программиорвания, управление, оптимальное управление, функциональные управления Беллмана.
2) Получить навыки и уметь: строить математическую модель ЗЦЛП; использовать различные методы для решения ЗЦЛП; анализировать полученные решения и находить альтернативные варианты при решении любым методом, интерпретировать полученные результаты в терминах решаемой задачи.
Условие задачи: коммерческая фирма закупила товары четырех наименований А1, А2, А3, А4 по десять упаковок каждого за пределами своего города. Доставку товаров предполагается осуществить собственным автофургоном за несколько рейсов. Грузоподъемность фургона – V кг, а стоимость С1, С2, С3, С4 тыс. руб.
Определить, какие виды товаров и в каком объеме необходимо перевести первым рейсом, с тем, чтобы их стоимость была максимальна.
![]()
Z=500![]() +450
+450![]() +470
+470![]() +510
+510![]() ->max
->max
8![]() +5
+5![]() +7
+7![]() +6
+6![]() <=46
<=46
![]() ,
,![]() ,
,![]() ,
,![]() >=0
и целые
>=0
и целые
Решим данную задачу с подошью PER:









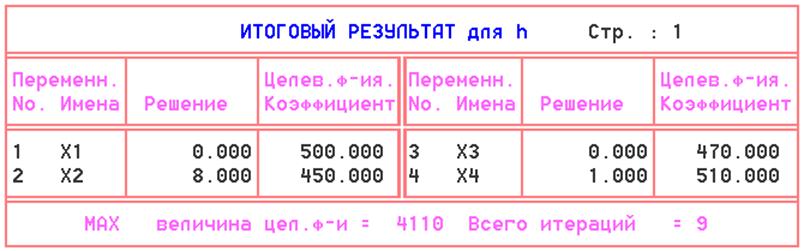
Постоим дерево решений метода ветвей и границ:
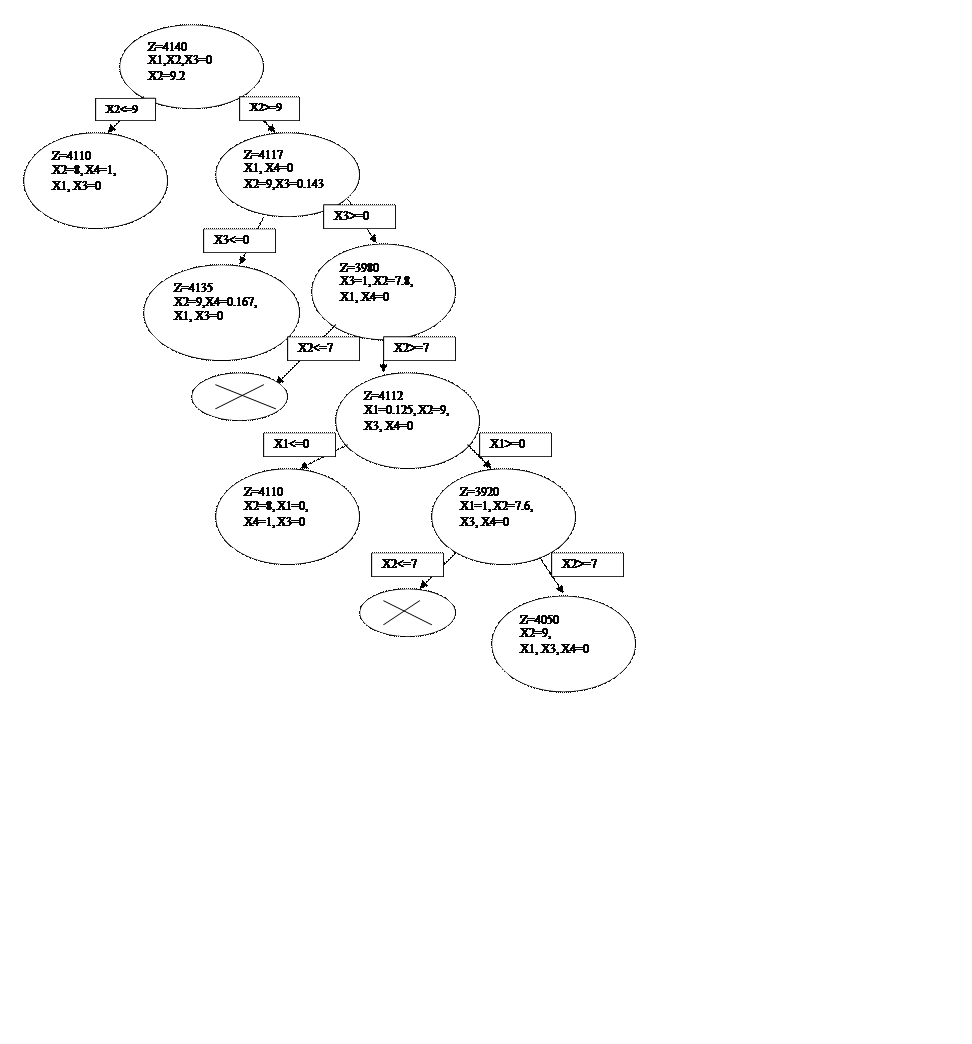
Таким образом, видно, что Z=max=4110 при X1=0, X2=8, X3=0, X4=1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.