Построение математической модели задачи о коммивояжере (бродячем торговце)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИ

Новосибирский Государственный Технический Университет

Расчетно-графическая работа №4

по курсу «Прикладные методы оптимизации»

вариант №3

Факультет бизнеса

Группа ФБИ

Студент

Преподаватель       Кириллов Ю.В.

Новосибирск

2007 г.

Цели задания:

1. Понимать смысл, различать, осознанно использовать следующие понятия: математическая модель задачи о коммивояжере (бродячем торговце); приведенная матрица расстояний, константы приведения, штрафы; множество допустимых решений задачи о коммивояжере, разбиение множества решений на подмножества, оценка подмножества решений, рекорд, дерево решений – в методе ветвей и границ для задачи о коммивояжере.

2. Получить навыки, уметь: строить математическую модель задачи о коммивояжере; решать задачу методом ветвей и границ; строить дерево решений; анализировать полученное решение и находить альтернативные варианты; интерпретировать полученные результаты в терминах решаемой задачи.

Условие задачи.

Коммивояжер должен объехать шесть городов и вернуться в исходный город. Расстояния между городами заданы матрицей .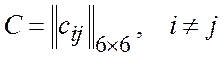

Определить маршрут коммивояжера, следуя которым он побывает в каждом городе только один раз, проехав при этом минимальное расстояние.

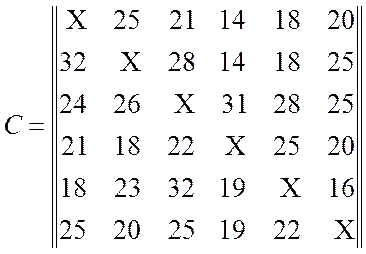
1.  Математическая модель задачи.

Z=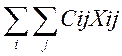 à MIN                     

Ограничения:                           

                               

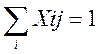
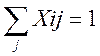
X – целые, положительные. Каждый город коммивояжер может посетить лишь единожды. Не должно быть замкнутых циклов.

2.  Решение задачи  методом ветвей и границ.

Найдём оценку снизу множества всех исходных маршрутов, делая приведение по строкам и столбцам:

	1	2	3	4	5	6	Ui
1	x	25	21	14	18	20	14
2	32	x	28	14	18	25	14
3	24	26	x	31	28	25	24
4	21	18	22	x	25	20	18
5	18	23	32	19	x	16	16
6	25	20	25	19	22	x	19

	1	2	3	4	5	6
1	x	11	7	0	4	6
2	18	x	14	0	4	11
3	0	2	x	7	4	1
4	3	0	4	x	7	2
5	2	7	16	3	x	0
6	6	1	6	0	3	x
Vj	0	0	0	0	0	0

Мы получили параметры приведения: U_i= 105, V_j =0.

Найдем константу приведения L₀=105+0=105.

Таким образом, Z₀>105 – оценка снизу целевой функции.

Найдём доплаты (штрафы) для каждого нулевого элемента и сравним их между собой:

Таблица 3

	1	2	3	4	5	6
1	x	11	7	04	4	6
2	18	x	14	04	4	11
3	03	2	x	7	4	1
4	3	03	4	x	7	2
5	2	7	16	3	x	03
6	6	1	6	01	3	x

Из всех нулевых элементов необходимо выбрать тот, у которого максимальна доплата (или степень нуля), т.к. она показывает величину экономии, которую мы будем иметь, если выберем маршрут, представленный этим нулевым элементом. По этому принципу на первом этапе выбираем маршрут (1,4).

1  2    3    4    5    6   1   x   x   x    x    x    x 2   18 x  14   x    4   11 3   03  2   x    x    4    1 4   x   03  4    x    7    2 5   2   7  16   x    x    03        6   6   1   6    x    3    x

1  2  3  4    5    6                                                   1    x  11  7   x    4    6                          2   18  x  14  0    4    11                            3   03   2    x   7   4    1                         4    3   03   4   x   7     2                          5    2   7   16  3    x    03                          6    6   1    6   01  3    x

1   2    3    4    5    6                             1   x   x   x    x    x    x   2   14 x  8     x    0   7   3   03  2   x    x    4    1   4   x   x    0    x    5    0   5   2   7  14   x    x    03   6   5   0   3    x    2    x

1    2    3    4    5    6   1    x   7   01   x    04    2  2   18  x   11  04   4    11    3   03   2    x   7     4    1 4    3   02   1   x     7     2  5    2   7   13  3     x     03  6    6   1    3   01   3     x

Z=105+9=114                                                                          Z₁⁽²⁾=105+7=112

Для дальнейшего ветвления выбираем то подмножество, которое имеет наименьшую оценку снизу, т.е. Z₁⁽²⁾=105+7=112.  

Теперь в таблице, которая соответствует подмножеству с оценкой Z₁⁽²⁾=112, необходимо выбрать маршрут, по которому это множество будет ветвиться на два. По максимальной степени нуля в этой таблице определяем, что следующим «кандидатом» в гамильтонов контур будет маршрут (1,5).

1    2    3    4    5    6   1    x   x   x   x     x    x  2   18  x   11  04   x    11    3   03   2    x   7     x    1 4    3   03   1   x     x     2  5    2   7   13  3     x    03  6    6   1    3   01   x    x

1    2    3    4    5    6   1    x   7   01   x    x    2  2   18  x   11  04   4    11    3   03   2    x   7     4    1 4    3   03   1   x     7     2  5    2   7   13  3     x    03  6    6   1    3   01   3    x