Реализация транспортной задачи в матричной постановке. Вариант № 8, страница 2

         По составленной таблице находим, что:  X = 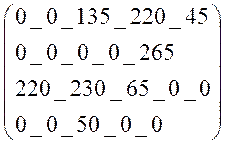 , а начальное     значение целевой функции будет следующим: Z =  135*14 + 220*12 + 45*15 + 265*10 + 220*12 +230*13 + 65*16 + 50*0 = 14525 тыс.руб.

3.  НОП, построенный методом минимального элемента.

     При использовании данного метода, необходимо в первую очередь заполнять клетки с наименьшим тарифом (т.е. когда затраты - минимальны) Т.о. в строке 1 мы заполняем клетку А₁В_4, но т.к. запасы превышают потребности – мы ищем следующую клетку, также с наименьшим тарифом (А₁В₃), но как только запасы на складе использованы полностью – мы больше не учитываем эту строку и т.д. Заполненная таблица имеет следующий вид: 

В из	В1	В2	В3	В4	В5	Запасы
А1	15	17	14        180	12 220	15	400
А2	17	11	13	11	10  265	265
А3	12    220	13     230	16    65	18	17	515
А4       (фиктивная)	0	0	0     5	0	0   45	50
Потребности	220	230	250	220	310

X =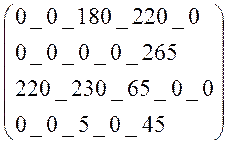 

   Z =  180*14 + 220*12 + 265*10 + 220*12 + 230*13 + 65*16 + 5*0 + 45*0 = 2520 + 2640 + 2650 +

          + 2640 + 2990 + 1040 + 0 + 0 = 14480 тыс.руб.

Для выбора дальнейшего решения найдем минимальное начальное значение целевой функции Z:

НОП = min (Z_min, Z_NWC, Z_VAM) = min(18645; 14525; 14480) = 14480 тыс.руб.

Т.о., опираясь на НОП, построенный методом минимального элемента, решим задачу методом потенциалов, позволяющим проверить полученное решение: является ли план оптимальным и единственен ли он.

Итак, исходная таблица:

В из	В1	В2	В3	В4	В5	Запасы
А1	15	17	14        180	12 220	15	400
А2	17	11	13	11	10  265	265
А3	12    220	13     230	16    65	18	17	515
А4       (фиктивная)	0	0	0     5	0	0   45	50
Потребности	220	230	250	220	310

Составим систему для вычисления цены покупки (α_i) и цены продажи (β_j) каждого вида ресурса, использованного для удовлетворения спроса потребителей.

Т.о.  для каждой занятой клетки напишем свое уравнение: β_j - α_i = с_ij, где с_ij  - тарифы перевозок, получаем: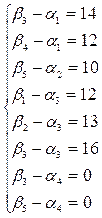

Т.к. у нас количество уравнений – 8, а количество переменных – 9, то чтобы решить данную систему, мы должны одну из переменных взять за ноль  (к примеру, мы

заземляем α₁), тогда получаем: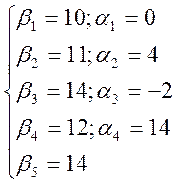

Теперь, зная значения α_i  и β_j , найдем рентабельность перевозки из i склада в j магазин (для свободных клеток), используя формулу r_ij = β_j –(α_i + c_ij ) = 0, получаем:

                        r₁₁ = β₁ – (α₁ + c₁₁ ) = 10 – 0 – 15 = -5;

                        r₁₂ = β₂ –(α₁ + c₁₂ ) = 11 – 0 – 17 = -6;

                        r₁₅ = β₅ –(α₁ + c₁₅ ) = 14 – 0 – 15  = -1;

                        r₂₁ = β₁ –(α₂ + c₂₁ ) = 10 - 4 – 17 = -11;

                        r₂₂  =β₂ –(α₂ + c₂₂ ) = 11 - 4 – 11 = -4;

r₂₃ = β₃ –(α₂ + c₂₃ ) = 14 – 4 – 13 = -3;

                        r₂₄ = β₄ –(α₂ + c₂₄ ) = 12 – 4 – 11 = -3;

                        r₃₄ = β₄–(α₃ + c₃₄ ) = 12 + 2 - 18 = -4;

                        r₃₅ = β₅ –(α₃ + c₃₅ ) = 14 + 2 – 17 = -1.

                        r₄₁ = β₁–(α₄ + c₄₁ ) = 10 - 14 - 0 = -4;

                        r₄₂ = β₂ –(α₄ + c₄₂ ) = 11 – 14 – 0 = -3.

                        r₄₄ = β₄ –(α₄ + c₄₄ ) = 12 – 14 – 0 = -2;

Т.к. у нас все полученные перевозки нерентабельны (все они равны отрицательным значениям), мы делаем вывод, что построенная начальная таблица является также и конечной таблицей, а значение целевой функции остается неизменным (Z =  14480 тыс. руб.). Т.е. опорный план является также и оптимальным планом! Но т.к., к сожалению, ПЭР не решает ТЗ методом минимального элемента, мы решим эту же задачу другим способом (для того, чтобы проверить правильность полученного решения). Возьмем, к примеру, НОП, построенный методом Фогеля (т.к. он является вторым по наименьшему значению начальной целевой функции.)

Итак, исходная таблица:

В из	В1	В2	В3	В4	В5	Запасы
А1	15	17	14        135	12    220	15  45	400
А2	17	11	13	11	10    265	265
А3	12 220	13  230	16      65	18	17	515
А4 (фикт.)	0	0	0      50	0	0	50
Потр.	220	230	250	220	310

Таким же способом составляем систему для вычисления цен покупки и продажи каждого вида ресурса, использованного для удовлетворения спроса потребителей: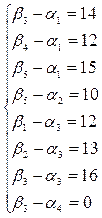     

Мы снова получили, что количество переменных не соответствует количеству уравнений, поэтому, как и раньше – принимаем за ноль  α₁, и получаем: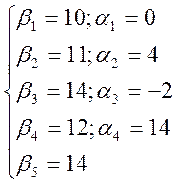

 

Аналогичным способом находим рентабельность перевозок, получаем:

                        r₁₁ = β₁ – (α₁ + c₁₁ ) = 10 – 0 – 15 = -5;

                        r₁₂ = β₂ –(α₁ + c₁₂ ) = 11 – 0 – 17 = -6;

                        r₂₁ = β₁ –(α₂ + c₂₁ ) = 10 – 5 – 17  = -12;

                        r₂₂ = β₂ –(α₂ + c₂₂ ) = 11 - 5 – 11 = -5;

                        r₂₃  =β₃ –(α₂ + c₂₃ ) = 14 - 5 – 13 = -4;

                        r₂₄ = β₄ –(α₂ + c₂₄ ) = 12 – 5 – 11 = -4;

                        r₃₄ = β₄ –(α₃ + c₃₄ ) = 12 + 2 – 18 = -4;