Реализация транспортной задачи в матричной постановке. Вариант № 8

МО и ПО РФ Новосибирский Государственный Технический Университет Кафедра экономической информатики Расчетно-графическая работа №2 по курсу «Теория оптимального управления в экономических системах» ТРАНСПОРТНАЯ ЗАДАЧА Вариант 8 Факультет: Бизнеса Группа: Студенты: Преподаватель: Кириллов Ю.В. Новосибирск 2003

Цели  задания:

1. понимать смысл, различать, осознанно использовать следующие понятия: транспортная задача (ТЗ) в матричной постановке; открытая и закрытая модели ТЗ; транспортная таблица, допустимый, опорный, оптимальный планы ТЗ; поставки, перераспределение поставок, потен­циалы строк и столбцов транспортной таблицы как двойственные оцен­ки; характеристики клеток транспортной таблицы, цикл пересчета; альтернативные решения ТЗ;

2. получить навыки, уметь: строить математическую модель ТЗ; переходить от открытой модели ТЗ к закрытой; использовать различ­ные методы для построения опорных планов ТЗ; решать ТЗ методом потенциалов; анализировать полученное решение и находить альтерна­тивные варианты; интерпретировать полученное решение в терминах

поставленной задачи.

   Условие задачи: транспортная фирма обслуживает n поставщиков однородного груза и m потребителей этого груза. В течение дня из каждого пункта пос­тавки фирма должна вывезти соответственно a₁, А₂,,.. , А_n тонн гру­за, а в каждый пункт потребления доставить соответственно В_i, В₂,..., В_m тонн. Себестоимость перевозки 1 тонны груза от i-го поставщика j-му потребителю составляет С_ij тыс. руб.

     Найти такой план перевозки грузов, при котором издержки транс­портной фирмы будут минимальными.

 Задание:записать математическую модель задачи. Построить опорные планы методом северо-западного угла, методом минимального элемента и ме­тодом Фогеля. Сравнить результаты. Опираясь на любой из полученных планов, решить задачу методом потенциалов. Решить задачу на ПЭВМ с помощью ПЭР и сравнить результаты с полученными ручным способом.

            Исходные данные для 8 варианта:        n=3,m=5;A₁=400,A₂=265,A₃=515;                 B₁=220,B₂=230,B₃=250,B₄=220,B₅=310;

                                                                           

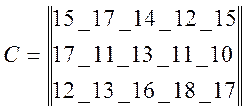
Чтобы решить данную задачу необходимо и достаточно, чтобы суммарная мощность всех поставщиков равнялась суммарной мощности всех потребителей, т.е. 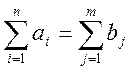, а т.к. у нас 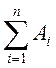< 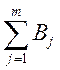, то есть запасов товара на складе меньше, чем потребности покупателей, то необходимо ввести дополнительного (фиктивного) поставщика А₅ = .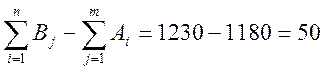

 Построим начальный опорный план (НОП) задачи 3 способами: методом северо-западного угла, методом Фогеля и методом минимального элемента. После каждой заполненной таблицы будем поверять условие ее невырожденности: ЧЗК = m + n –1. Если оно не выполняется, выбираем любую свободную клетку и заносим в нее 0, считая занятой, так, чтобы не образовалось цикла из занятых клеток.

1.  НОП, построенный методом северо-западного угла.

      Используя данный метод, мы должны начинать заполнять таблицу с верхнего левого угла (это следует из названия метода). Т.о. мы выбираем клетку А₁В₁ и заполняем ее числом  220_, т.к. именно столько у нас потребностей покупателей для данного вида товара (следовательно, больше мы первый столбец не учитываем). Аналогично заполняем следующие клетки, начиная всегда с верхнего левого угла.

В из	В1	В2	В3	В4	В5	Запасы
А1	15 220	17       180	14	12	15	400
А2	17	11     50	13    215	11	10	265
А3	12	13	16    35	18 220	17   260	515
А4       (фиктивная)	0	0	0	0	0   50	50
Потребности	220	230	250	220	310

                                                   X =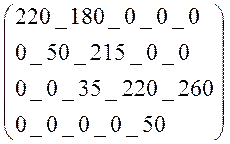  

Z = 220*15 + 180*17 + 50*11 + 215*13 + 35*16 + 220*18 + 260*17 + 50*0 = 18645 тыс.руб.

2.  НОП, построенный методом Фогеля.

В из	В1	В2	В3	В4	В5	Запасы	Δ	Δ		Δ		Δ	Δ		Δ
А1	15	17	14        135	12    220	15 45	400	2	2		2		1	1		1
А2	17	11	13	11	10    265	265	1	1		-		-	-		-
А3	12 220	13  230	16      65	18	17	515	1	1		1		1	4		1
А4 (фикт.)	0	0	0      50	0	0	50	0	-		-		-	-		-
Потр.	220	230	250	220	310
Δ	12	11	13	11	10
Δ	3	2	1	1	5
Δ	3	4	2	6	2
Δ	3	4	2	-	2
Δ	3	-	2	-	2
Δ	-	-	2	-	2

     Чтобы построить начальную таблицу методом Фогеля, необходимо сначала найти разность между двумя наименьшими тарифами для каждой строки и столбца (соответственно: Δ и Δ) После чего из полученных результатов находим наибольшее значение [в нашем случае -  это число 13] и начинаем заполнение таблицы именно с этой строки\столбца [у нас - столбец В₃]. В найденной строке/столбце находим наименьший тариф и заполняем данную клетку [А₄В₃]. Затем аналогичным способом  заполняем следующие клетки, при условии, что если потребности покупателя удовлетворены полностью или запасы на складе полностью использованы,  мы больше не учитываем соответствующий столбец/строку при расчете Δ. Полученная таблица выглядит следующим образом: