Определение радиуса кривизны линзы и длины световой волны с помощью колец Ньютона

Работа 33

ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ И ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА

Цель работы. Изучение явления интерференции света и определение радиуса кривизны линзы и длины световой волны с помощью колец Ньютона.

Приборы и принадлежности: микроскоп с окулярной шкалой; осветитель и два светофильтра; оптическая система из плоско - выпуклой линзы и плоскопараллельной пластинки.

Введение

Рассматривая свет как электромагнитную волну, распространяющуюся в пространстве, для напряженностей электрического и магнитного полей E и H можно записать следующие зависимости от времени и расстояния от источника;

E = Ecos(t - kr +j₀) ,                                                       (1)

                                                  H = Hcos(t - kr +j₀) ,                                                      (2)

где E и H - максимальные значения векторов;  - циклическая частота; t - время; k = 2  - волновое число;  - длина волны; r – расстояние, отсчитываемое вдоль направления распространения плоской волны;  - начальная фаза колебаний.

Так как физиологическое, фотоэлектрическое и фотохимическое воздействия оказывает напряженность электрического поля, то обычно для световой волны ограничиваются записью одного уравнения

E = Acos(t- kr+j₀),

где А - амплитуда вектора E; (t - kr +j₀) - фаза колебания.

При распространении света в однородной среде можно считать, что интенсивность света I в данной точке пропорциональна квадрату амплитуды световой волны:

I ~ A .                                                      (3)

При наложении двух плоских волн с одинаковой частотой E=Acos(t - k₁r +j₀₁)    и   E=Acos(t - k₂r +j₀₂), распространяющихся в одном направлении, амплитуда результирующего колебания в данной точке определяется следующим выражением:

A= A + A +2AAcos,

где  - разность фаз колебаний.

Интересная картина наблюдается при сложении когерентных волн. Когерентностью называется согласованное протекание во времени и в пространстве нескольких колебательных или волновых процессов, проявляющееся при их сложении. Колебания называют когерентными, если разность их фаз остается постоянной во времени и при сложении колебаний определяет амплитуду суммарного колебания.

Согласованность колебаний во времени называют временной когерентностью. Согласованность колебаний в пространстве называют пространственной когерентностью (см. приложение к данной работе).

В соответствии с выражением (3) интенсивность света имеет для каждой точки пространства определенное значение

I = I+ I+2 cos,                                        (4)

зависящее от cos. Последний член выражения (4) называют интерференционным членом.

В точках пространства, где cos<0, интенсивность I будет меньше I+ I; в точках пространства, где cos>0, величина I будет больше, чем I+ I т.е. при наложении когерентных волн будет происходить перераспределение света в пространстве: в одних местах будет наблюдаться усиление, в других - ослабление. Наложение когерентных волн, сопровождающееся возникновением максимумов и минимумов интенсивности, называется  интерференцией.

В случае наложения некогерентных волн значение  непрерывно изменяется и среднее по времени значение cos будет равно 0. В этом случае не возникает устойчивой интерференционной картины, а во всех точках пространства наблюдается одинаковая интенсивность, равная сумме интенсивностей Iи I.

Получить интерференционную картину от двух различных источников света, имеющих одинаковое монохроматическое излучение при обычных механизмах их возбуждения (тепловое излучение, люминесценция), нельзя, т.к. даже почти точечный источник монохроматического света содержит огромное число атомов - излучателей с различными фазами колебаний, что исключает согласованность их излучения.

Обычно когерентные световые волны получают делением одного потока, идущего от какого - либо источника света, на два потока. После прохождения волнами разных путей между ними образуется разность фаз. При интерференции полученных таким образом волн наблюдается устойчивая интерференционная картина. Впервые такой способ предложил Юнг в начале 19 столетия. Источник монохроматического света S (рис. 1) освещает два очень маленьких и близко расположенных отверстия на экране А.

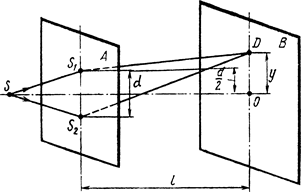Рис. 1

По принципу Гюйгенса-Френеля отверстия S и S можно считать двумя когерентными источниками излучения, так как SS= SS, то фазы колебаний в S и S одинаковы.

Если на некотором расстоянии от экрана А находится экран В, то в какую - либо точку экрана (например, в точку D) световые волны от S и S будут приходить, имея определенную разность фаз, которая зависит от разности расстояний SD - SD называемой разностью хода. При разности хода, равной четному числу полуволн, фазы колебаний, приходящих в точку D, будут совпадать, и в этой точке будет максимум освещенности. В тех точках экрана, для которых разность хода окажется равной нечетному числу полуволн, фазы колебаний будут противоположны и следовательно, будет минимум освещенности. В точке О наблюдается максимум освещенности, так как разность хода лучей от S и S равна нулю.

Если волны, посылаемые когерентными источниками света, монохроматичны, то на экране картина будет представлять собой чередование темных и светлых полос. Практически для этого достаточно пропустить свет через цветное стекло - светофильтр. Если же источник посылает белый свет, то интерференционная картина представляет собой чередование цветных полос, причем полной темноты не будет нигде, так как места минимумов для одной длины волны совпадают с местами максимумов для другой.

Из геометрических соотношений нетрудно установить, в каких точках экрана B будет наблюдаться максимум и минимум освещенности. В оптике оптической длиной пути называют геометрическую длину пути l, умноженную на абсолютный показатель преломления n . Тогда разность оптических длин путей интерферирующих волн

 = .

Используя рис. 1 и считая, что оба луча SD и SD распространяются в воздухе, для которого n = 1, получим разность хода на удаленном экране (l l₁ l₂)

 .

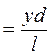Максимум освещенности будет в точках, где разность хода равна четному числу полуволн

,

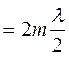где  - длина световой волны, m - любое целое число. Если вычисленная разность хода равна нечетному числу полуволн, т.е.

,

то в соответствующих точках будем иметь минимум освещенности.

Рассмотрим интерференционную картину, которая возникает при отражении света от двух поверхностей очень тонкого клина c углом при вершине  (Рис. 2).

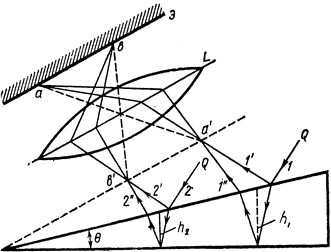Рис. 2

Пусть на клин падает параллельный пучок лучей Q, из которого выделим лучи 1 и 2. Каждый из выделенных лучей расщепляется на два луча в результате отражения от верхней и нижней поверхностей клина: 1’ и 1’’  и  2’ и 2’’. Отраженные лучи  1’  и  1’’  являются когерентными и будут пересекаться в точке a’, а лучи  2’  и  2’’  также когерентны и пересекаются в точке b’. В этих точках лучи встречаются, имея разность хода, определяемую толщиной h для лучей 1’ и 1’’, и толщиной h для лучей 2’ и 2’’. Если на пути отразившихся лучей поставить линзу L (роль линзы может выполнять хрусталик глаза), то линза отобразит на экране Э плоскость a’ - b’, в которой пересекаются отраженные лучи, и на экране Э будет наблюдаться интерференционная картина (роль экрана может выполнять сетчатка глаза).

Если наблюдать интерференционную картину со стороны ребра клина, то картина локализуется над клином (рис. 2).

При нормальном падении лучей 1 и 2 на нижнюю поверхность клина полосы равной толщины будут локализованы на верхней поверхности клина.