Определение радиуса кривизны линзы и длины световой волны с помощью колец Ньютона, страница 2

Так как каждая из интерференционных полос одной разности хода образуетсяется за счет отражений от мест клина, имеющих одинаковую толщину, то интерференционная картина называется полосами равной толщины. Полосы равной толщины можно наблюдать при освещении плоско - выпуклой линзы малой кривизны, расположенной на плоскопараллельной пластине (Рис. 3).

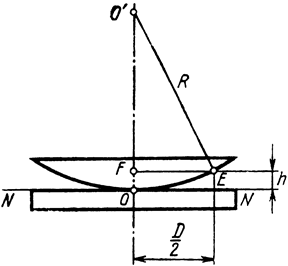
     Рис.3

Роль клина при этом выполняет воздушный зазор между линзой и плоскопараллельной пластиной, утолщающийся от точки их соприкосновения к краю линзы. При падении монохроматического света нормально к плоской поверхности линзы и поверхности пластины интерференционная картина имеет вид концентрических темных и светлых колец, которые называют кольцами Ньютона, так как он впервые их наблюдал и описал. Разность хода лучей , отражающихся от верхней и нижней поверхностей клина, равна примерно удвоенной толщине воздушного клина 2h. Следует также учесть, что при отражении волны от оптически более плотной среды (больший n) на границе NN воздух - стекло, т.е. от нижней пластины, фаза ее меняется скачком на  радиан, что соответствует возникновению дополнительной разности хода между интерферирующими лучами, равной  .

Полная разность хода  будет, таким образом, складываться из удвоенной толщины клина и половины длины волны:

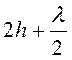= .                                           (5)

Интенсивность интерферирующих лучей  в точке E (см. рис. 3) будет минимальной, если разность хода  составляет нечетное число полуволн:

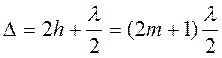 ,                               (6)

где  m - 0, 1, 2, 3, ... .

Таким образом, минимум интенсивности будет наблюдаться для всех точек воздушного слоя, где

.                                              (7)

Геометрическое место этих точек образует кольцо диаметром D. Наблюдаемые интерференционные кольца являются полосами равной толщины.

В месте соприкосновения линзы с пластиной остается очень маленькая воздушная прослойка, толщина которой гораздо меньше длины волны, поэтому в формуле (5) 2h приблизительно равно 0, и разность хода  равна только  за счет потери полуволны при отражении от оптически более плотной среды (пластинки). В результате этого мы и наблюдаем в отраженном свете в центре минимум освещенности, т.е. темное пятно.

Найдем связь между радиусом кривизны линзы R, диаметром кольца D и длиной световой волны. Из треугольника О’FE (см. рис. 3) для кольца с номером m имеем

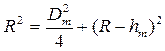.                                    (8)

Делая преобразование уравнения (8) и считая  малым по сравнению с 2R, получим

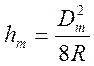                                                           .                                                                      (9)

Решая совместно уравнения (9) и (7), получим

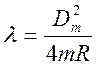                                                     .                                                                     (10)

Практически, вследствие упругой деформации стекла невозможно добиться идеального соприкосновения линзы с пластиной в одной точке, поэтому более правильный результат получится, если вычислять  не по одному кольцу, а путем сравнения диаметров двух колец по формуле

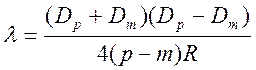,                              (11)

где p и m - номера темных колец;  и  - соответственно их диаметры.

В данной работе, применяя формулу (12), сначала определяют радиус кривизны неизвестной линзы при известной длине волны красного света:

R =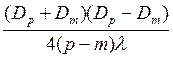 .                                 (12)

Затем по формуле (11) определяют длину волны другого монохроматического света (зеленого).

Монохроматический свет, используемый в данном опыте (красный и зеленый), получают, пропуская белый свет через соответствующие светофильтры.

Методика измерений

На столик измерительного микроскопа (рис. 4) поместить плоско - выпуклую линзу с плоскопараллельной пластиной в оправе 2, таким образом, чтобы кольца попали в поле зрения микроскопа. В окуляре 3 микроскопа помещается отсчетная шкала 4 (окулярный микрометр), с помощью которого можно определять диаметры колец Ньютона. Цена деления шкалы указывается на микроскопе.

Перемещением тубуса 5 микроскопа по вертикали с помощью винта 6 добиться резкости интерференционной картины. К тубусу микроскопа приделана камера 7, в которой помещается лампа накаливания 8 и поставленная под углом 45° к оси микроскопа полупрозрачная пластина 9. В камере 7 имеется щель, в которой помещаются светофильтры 10 для того, чтобы из белого пучка света лампы накаливания выделять монохроматические лучи.

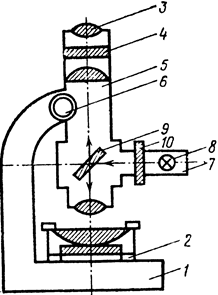
Рис.4

Порядок выполнения работы

1.  Включить лампу накаливания.

2.  На пути лучей от лампы накаливания установить красный светофильтр.

3.  На столике микроскопа поместить оправку с линзой и пластиной таким образом, чтобы кольца располагались концентрично относительно поля зрения микроскопа. Кольца установить так, чтобы шкала проходила через их центр. Перемещением тубуса микроскопа по вертикали добиться резкости интерференционной картины.

4.  Измерить диаметры колец в двух взаимноперпендикулярных направлениях, поворачивая окуляр на 90 градусов. Записать в табл. 1 числовые отметки окулярной шкалы, относящиеся к двум точкам каждого темного кольца. Темное пятно в середине соответствует нулевому порядку m = 0.