Методические указания к лабораторным работам "Резонанс напряжений в колебательном контуре" и "Резонанс токов в колебательном контуре", страница 3

4.  Включить  вольтметр  в  положение  V₃,  для измерения напряжения на  активном  сопротивлении,  которое  пропорционально силе тока в контуре.

5.  Все  предыдущие  задания  выполняются  при отключенном  источнике  тока  e.  Перед  началом  измерений   все  конденсаторы должны быть выключены.

6.  Включить   источник  тока   и  провести   измерения  напряжения  на  активном  сопротивлении,  включая  в   контур  один конденсатор, потом два, три и т. д. Когда  емкость батареи станет  максимальной,  повторить  те  же   измерения,  по одному  выключая  конденсаторы   из  батареи.   Записав  измеренные напряжения в таблицу, выключить источник тока.

7. Построить график зависимости  и определить по нему  частоту   n_р,  при  которой  наблюдается  максимум напряжения  на  активном  сопротивлении  и,  следовательно,  силы тока в контуре.

8.  Включить  вольтметр  в  положение  V₁,  для измерения напряжения     на емкости и,  следуя п.п.  5 и  6, провести измерения.                                                     

       9.  Включить  вольтметр  в  положение  V₂  для измерения напряжения   на  индуктивности и,  следуя п.п.  5 и  6, провести измерения.                                              

       10. Построить графики зависимости    (n)  и  (n) .

 Объяснить особенности распределения напряжения на разных участках  колебательного контура  при резонансе  и при   подходе к нему.                                                            

       11.  Составить батарею конденсаторов, обеспечивающую получение в контуре резонансной частоты, после  чего включить вольтметр к точкам а и b  для измерения напряжения  на участке, содержащем индуктивность  и емкость:   Включить  источник  тока и  измерить несколько  раз напряжение , записав в отчет ero среднее значение. Выключить источник тока.                                                 

       12. Сравнить напряжения   , при резонансной частоте.         

Результаты измерений

Параметры	Номер измерения
	1	2		10
Емкость батареи С, mФ
Частота собственных колебаний, n, Гц
Напряжение
Напряжение
Напряжение

         L = ...............Гн;      = ..................В.                                   

Контрольные вопросы

1. В чем состоит резонанс напряжений в контуре?                       

2. Выведите формулу для амплитуды силы тока установившихся вынужденных колебаний в контуре.

3.  Выведите  формулу  для  сдвига  фаз  между  силой  тока в  контуре и  вынуждающей ЭДС.                                                          

4. Чему равна разность фаз между силой тока в контуре  и вынуждающей ЭДС при резонансе?                                                 

5. Чему равна разность фаз напряжений на  катушке индуктивности и на батарее конденсаторов?                                 

Литература

  Савельев И.В. Курс общей физики. Т. II. – М.: Наука, 1993.

   Детлаф А.А., Яворский Б.М., Курс общей физики. – М.: Высшая школа, 2000.

Работа № 77

РЕЗОНАНС ТОКОВ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Цель работы: изучение распределения токов в различных ветвях электрического контура при резонансной и близких к ней частотах.

Введение

Резонанс токов возникает при определенных условиях в электрическом контуре, содержащем параллельно включенные катушку индуктивности L и конденсатор емкостью C (рис.1). Активные сопротивления в ветвях обозначены R₀, R₁ и R₂. В контур включается источник тока, ЭДС которого зависит от времени по гармоническому закону

.

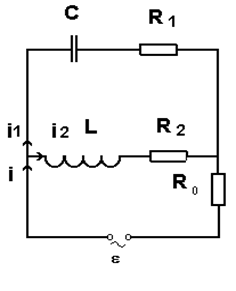
Рис. 1

Резонанс токов сопровождается рядом интересных особенностей, которые можно установить при расчете токов в схеме рис. 1 и проверить экспериментально. Предполагая, что величина циклической частоты вынуждающей ЭДС W и размеры электрического контура обеспечивают квазистационарность токов, применим правило Кирхгофа для выяснения характера установившихся вынужденных колебаний тока в этом контуре. Для мгновенных значений токов, сходящихся в узле, используя первое правило Кирхгофа можно написать равенство

i=i₁+i₂ .                                                      (1)

При составлении уравнений для контуров воспользуемся уравнением (2) работы № 76, теоретическую часть которой необходимо изучить, приступая к подготовке данной лабораторной работы. Запишем это уравнение

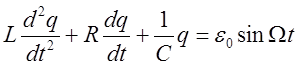.                        (2)

Нетрудно видеть, что уравнение для контура, содержащего С, R₁, R₀ и e (см. рис.1), получается из уравнения (2), если принять L=0, R₀=0 и R=R₁:

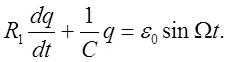
Используя решение уравнения (2) в работе № 76, получим для силы тока i₁ следующее выражение:

.

Амплитуда силы тока i₀₁ и сдвиг по фазе между током и вынуждающей ЭДС a₁ имеют вид

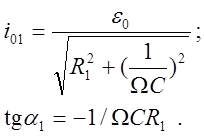                                  (3)

Для контура, содержащего L, R₂, R₀ и e, из уравнения (2) в предположении, что , R₀=0 и R=R₂, получим уравнение

.

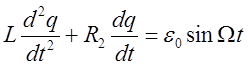Из этого уравнения следует такое выражение для силы тока i₂:

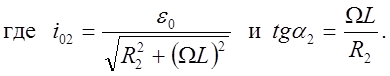                  (4)

Так как циклическая частота W токов i₁ и i₂ при установившихся вынужденных колебаниях одинакова, то согласно формуле (1) силу тока i можно представить в виде

      (5)

   

Как видно из формул (3-5), сила токов в ветвях и фазовые соотношения между ними и ЭДС определяются параметрами L, C, e₀, W, R₁ и R₂.

Известно, что наиболее выразительно явление резонанса проявляется при отсутствии активного сопротивления. Допустим для этого предельного случая, что R₁=R₂=0. Тогда

При этом амплитудное значение тока в неразветвленной части цепи оказывается наименьшим:

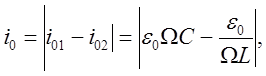
а токи в ветвях (i₁ и i₂) изменяются противофазно. Из последнего равенства вытекает условие, при котором ток в неразветвленной части цепи обращается в нуль. Для этого необходимо, чтобы частота вынуждающей ЭДС стала равной собственной частоте колебаний идеального контура (содержащего индуктивность и емкость).