Методические указания к лабораторным работам "Резонанс напряжений в колебательном контуре" и "Резонанс токов в колебательном контуре", страница 2

Как видно из уравнений (8) и (9), амплитуда силы тока  и сдвиг фаз зависят не только от параметров контура, но и от частоты вынуждающей ЭДС. При этом легко определить частоту, при которой реактивное сопротивление становится  равным нулю:

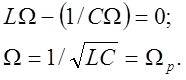
  Эта частота   W_p, как видно, совпадает с частотой собственных незатухающих колебаний в контуре и называется резонансной, так как ей соответствует максимальное значение амплитуды силы тока                                                

и  нулевое  значение  сдвига фаз  между током  и вынуждающей  ЭДС.  Явление  резкого  возрастания  амплитуды  силы тока  и  сближения  фаз  колебаний  тока и  вынуждающей ЭДС при  приближении  частоты   вынуждающей  ЭДС   к  собственной частоте колебаний в контуре называется  резонансом. Он сопровождается не только отмеченными, но и  рядом других  характерных особенностей.  Рассмотрим, в  частности, напряжение при резонансной частоте сначала на  концах катушки индуктивности, а затем между обкладками конденсатора:

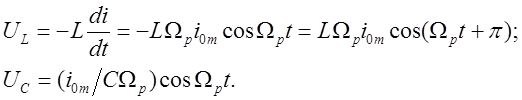
Сравнение этих двух напряжений показывает, что амплитуды их при резонансе совпадают, а фазы колебаний противоположны. Значит, в условиях резонанса , а напряжение на активном сопротивлении должно быть максимальным. Этот вид резонанса и называют резонансом напряжений.

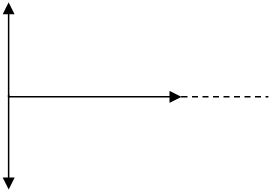
 Векторная  диаграмма  для  случая резонанса  напряжений показана на рис. 3.   

 

                                                                                

                                           e₀               ось

                                          Ri₀            токов

                     

Рис. 3

Резонансная частота для заряда q и напряжения  равна:

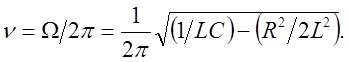
В  данной  работе должны  быть  экспериментально изучены  отмеченные  выше  особенности   распределения  напряжений  на  разных участках  колебательного контура  при резонансе и при подходе к нему.                              

Описание установки

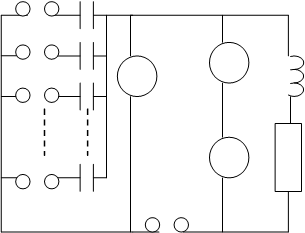
    Колебательный контур  состоит из  последовательно соединенных  катушки  индуктивности,  батареи  конденсаторов  и активного сопротивления (рис. 4).

              C

                    

V1

                                       V₂            

                                                         L  

                           а              б 

V3

   

                                              R

                            ~e

Рис. 4

 С  помощью  трансформатора,  включаемого  в  сеть  с напряжением  220  В, к  этому контуру  подводится напряжение 6,3  В, выполняющее  роль  вынуждающей  ЭДС.  Так  как вынуждающая  ЭДС имеет постоянную  частоту  50  Гц, то подход  к  резонансу  может  осуществляться  изменением собственной частоты колебаний в контуре. Для получения нескольких собственных частот колебаний  в схеме  имеется набор  конденсаторов,  параллельное соединение  которых позволяет   изменить   величину   емкости   в   контуре   в  широких пределах.                                                      

Собственная частота свободных электромагнитных колебаний в контуре определяется по формуле:

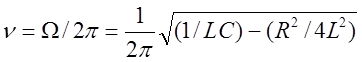.                (10)

В  данной  работе  параметры  L,  R и С  подобраны так,  что пренебрежение   вторым   слагаемым  под   корнем  приводит   к  неточности  в  расчете  частоты,  не  превышающей  1%   от  величины n. Поэтому   рекомендуется  рассчитывать   частоту  собственных колебаний по формуле                                  

 .                                     (11)

Для  измерения  нaпpяжений   на  различных   участках  контура   можно   пользоваться   одним    вольтметром,   включаемым при  выполнении  разных  заданий  так,  как вольтметры  V₁, V₂, V₃ на  рис.4. Для измерения  напряжения на  индуктивности и емкости  вместе  подключают  вольтметр  к  клеммам  ab.  В  этом случае  измеряемое  при   резонансе  напряжение   +   может  оказаться   не  равным   нулю,  а   лишь  во   много  раз меньшим,  чем  напряжение   на  индуктивности   или  емкости порознь.  Это, объясняется,   во-первых,  тем,   что  скачкообразное   изменение  емкости   не  гарантирует   получения  резонансной  частоты  с  высокой  степенью  точности,  что   может  сказаться  на  разности  фаз  напряжений    и    и, во-вторых, тем,  что  катушка  индуктивности  содержит  много  витков  проволоки,   обладающей   активным   сопротивлением,   не  достаточно малым по сравнению с R.                                     

    При  этом  заметим,  что  в  колебательном  контуре,  на  который   подается   напряжение   с   различным  W,  максимальные значения    и   достигаются  при   частотах,  отличных от W_р.  В  данной  работе,  в  которой  мы  меняем   не  частоту внешнего   напряжения,   а   емкость  системы,   это  проявляется в    следующем.    Амплитуда   напряжения    на   индуктивности =  = от  величины емкости С зависит так   же, как   и  амплитуда   напряжения  на   активном  сопротивлении  .  Поэтому   своего   максимального   значения  достигает одновременно   с   . Амплитуда   напряжения  на емкости и  при  увеличении емкости  С  уменьшается  быстрее,  чем  напряжение  . Поэтому максимальное  значение   достигается  при   величине  емкости  меньшей,  чем  величина  емкости,  при  которой достигается максимальное значение .                                                               

       Приборы   и   принадлежности:  колебательный   контур  из последовательно   соединенных   катушки   индуктивности,  активного   сопротивления,   батареи   конденсаторов,  вольтметр, провода.                                                      

                    Порядок выполнения работы

1.  Ознакомиться  с  установкой  и  дополнительными указаниями   к   ней,   содержащими  значения   параметров  данного контура. Величину индуктивности записать в таблицу.

2.  По  известным  емкостям отдельных  конденсаторов рассчитать и  записать в  таблицу емкости  батарей, составленных из  одного, двух,  трех, и т.  д. конденсаторов  (при параллельном соединении емкости конденсаторов суммируются).  

3. По  формуле (11)  рассчитать частоты  собственных колебаний контура и записать их в таблицу.