Исследование электропроводности полупроводников. Исследование проводимости полупроводников с собственной и примесной проводимостью

                                          Р А Б О Т А    №71в

Исследование электропроводности полупроводников

   Целью работы является изучение статистики Ферми-Дирака, исследование проводимости полупроводников с собственной и примесной проводимостью.

Введение

   Электрический ток, обусловленный движением электронов по кристаллу под действием электрического поля, есть неравновесный процесс, которому соответствует неравновесная функция распределения электронов. Но, поскольку, электропроводность обусловлена небольшим количеством электронов, расположенных вблизи уровня Ферми, для описания поведения электронов в кристаллах часто используют равновесное распределение Ферми-Дирака [1,2]:

                                              f(E) =  {exp [(E – Е_F) /kT] + 1}^–1,                                     (1)

где Е – энергия электронов, Е_F – энергия Ферми, Т – абсолютная температура.

   В полупроводниках с собственной проводимостью уровень Ферми лежит посередине запрещенной зоны [1]:

                                                            E – Е_F = Е_g/2 ,                                                        (2)

где E_g – ширина запрещенной зоны, величина которой порядка 1 эВ. При комнатной температуре произведение kT≈0,025 эВ, а следовательно ехр[(E – Е_F) /kT] >> 1 и распределение (1) в этом случае можно представить в виде:

                                                       f(E) =  exp ( – Е_g /2kT).                                              (3)

Так как при собственной проводимости концентрация дырок в валентной зоне равна концентрации электронов в зоне проводимости, статистика Ферми-Дирака позволяет рассчитать концентрацию электронов в зоне проводимости и получить выражение для собственной удельной проводимости полупроводников [1]: 

                                                 σ = en(u_n+u_p) =  σ₀ exp(-E_g/2kT) ,                                           (4)

где е – заряд электрона, n – концентрация электронов, u_n и u_p – подвижности электронов и дырок, коэффициент σ₀ имеет смысл удельной электропроводности при Т→ ∞ и определяется энергией Ферми полупроводника. Зависимость σ₀ от температуры, по сравнению с экспонентой, является слабой и здесь ее можно не учитывать. Из (4) следует, что электрические свойства собственного полупроводника практически полностью определяются шириной его запрещенной зоны и температурой.

   Для полупроводников с примесной проводимостью донорный уровень расположен в запрещенной зоне вблизи дна зоны проводимости, а акцепторный уровень вблизи потолка валентной зоны, на расстояниях Е_а≈ E_d ~ 0,01÷0,1 эВ, которые носят название энергии активации. При Т=0К величина энергии Ферми составляет E_F(0) = E_d/2 = Е_а/2. При этом сам уровень Ферми располагается посередине между дном зоны проводимости и уровнями донора Е_d (в случае донорной примеси) или посередине между потолком валентной зоны и акцепторным уровнем Е_а (в случае акцепторной примеси). Поэтому при невысоких температурах проводимость  определяется донорной или акцепторной примесью [1]:

                                                 σ_e = σ_d exp(-E_d/2kT),                                                  (5)

или

                                                 σ_р = σ_а exp(-E_а/2kT) .                                                 (6)

По мере повышения температуры концентрация примесных электронов в зоне проводимости растет сначала экспоненциально и проводимость полупроводника определяется выражениями (5) или (6). Затем, когда все примесные электроны оказываются выброшенными в зону проводимости, наступает насыщение зависимости n(Т) и поведение функции σ(Т) определяется температурной зависимостью подвижности носителей заряда. Дальнейшее увеличение температуры приводит к преобладанию межзонных переходов (т.е. переходам электронов из валентной зоны в зону проводимости) и проводимость полупроводника определяется собственной проводимостью (4). При этом уровень Ферми будет перемещаться к середине запрещенной зоны, около которой он расположен в случае собственного полупроводника.

Методика эксперимента и описание установки

Выражения (4), (5) и (6), полученные с использованием статистики Ферми-Дирака, могут быть проверены экспериментально. На рис.1 схематично изображена экспериментальная установка.

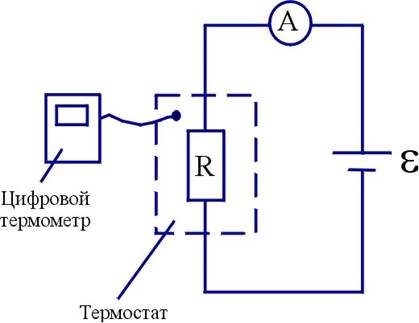
Рис. 1. Блок-схема экспериментальной установки.

Полупроводниковый образец сопротивлением R подключают к источнику напряжения e и помещают в термостат. В установке предусмотрена возможность плавного изменения температуры термостата и ее измерения цифровым термометром. Поскольку ток в цепи пропорционален проводимости полупроводника, то выражение (4) можно записать в виде:

                                                    I = I₀ exp(-E_g/2kT) ,                                                    (7)

где I₀ – коэффициент слабо зависящий от температуры.

   Из (7) получаем:

                                               ln( I  ) = - (E_g/2k) T^-1 + ln( I₀ ),                                        (8)

   Изменяя температуру термостата и измеряя ее цифровым термометром, снимают величину тока в цепи полупроводникового сопротивления с собственной проводимостью при постоянном напряжении e. По результатам измерений строится график зависимости ln( I ) от Т^-1 (рис.2). Тангенс угла наклона этой прямой определяется величиной энергии запрещенной зоны, что позволяет вычислить значение E_g.

Рис.2  Зависимость логарифма тока от величины обратной температуре

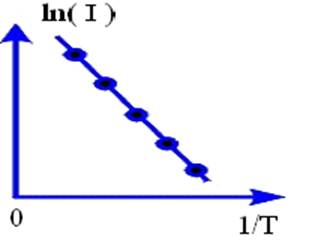
для полупроводников с собственной проводимостью.

   Линейная зависимость (8) во всем диапазоне температур свидетельствует о сохранении собственной проводимости полупроводника. Если исследуется полупроводник с примесной проводимостью, то