













Имеем дело с дискретной информацией с объемом
алфавита М. Сообщения закодированы и есть два крайних случая представления их в
виде сигналов. Первый вариант двоичное кодирование символов алфавита (нумерация
знаков), номеру сопоставляется ![]() -разрядная (
-разрядная (![]() ) последовательность сигналов.
Сигналов 2, они различаются. Второй вариант – М-ичное кодирование. Каждой букве
свой сигнал длительностью
) последовательность сигналов.
Сигналов 2, они различаются. Второй вариант – М-ичное кодирование. Каждой букве
свой сигнал длительностью ![]() :
: ![]() .
.
Как в общем случае получить множество сигналов для
передаваемых символов. Предлагается следующий метод. Задается ![]() - ортонормированных колебаний
- ортонормированных колебаний ![]() . Ортонормированность означает
. Ортонормированность означает 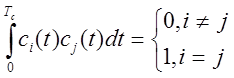 .
.
Каждому символу алфавита сопоставляется вектор
(набор чисел) ![]() .
.
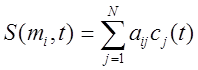 .
.
Это общее правило формирования сигналов практически не накладывает ограничений на выбор системы сигналов.
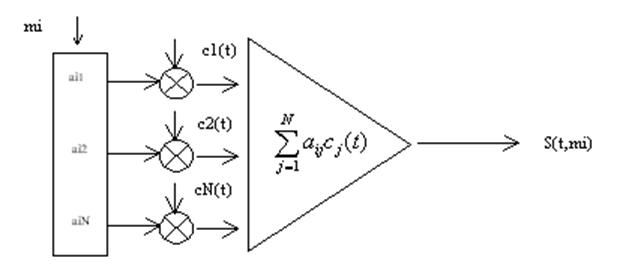
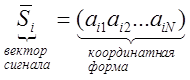
Зная ![]() и систему
ортогональных сигналов, мы однозначно получили сигнал
и систему
ортогональных сигналов, мы однозначно получили сигнал ![]() .
Как из сигнала извлечь, что именно передавалось. Вычислим интеграл:
.
Как из сигнала извлечь, что именно передавалось. Вычислим интеграл:
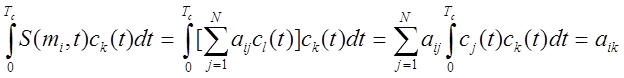 .
.
Проведя интегрирование по всем ![]() ,
, ![]() получается
получается
![]() в координационной форме.
в координационной форме.
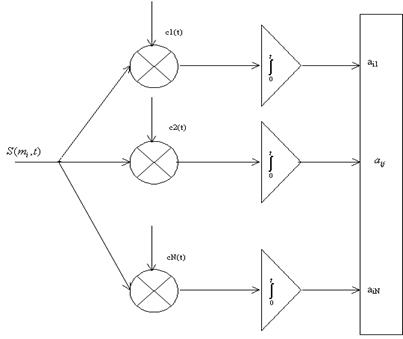
Следовательно, имея в точке приема генераторы ![]() синхронные и синфазные с
генераторами на передаче, выделяем информацию, причем безошибочно (если нет
помех), т.к. получаются последовательности
синхронные и синфазные с
генераторами на передаче, выделяем информацию, причем безошибочно (если нет
помех), т.к. получаются последовательности ![]() как
на передающем конце совпадающие с теми или иными символами.
как
на передающем конце совпадающие с теми или иными символами.
Если есть помехи, то на входе будет
![]() .
.
Получаем  .
.
Восстановленный вектор не совпадает ни с одним из передаваемых. Значит, задача приема есть задача распознавания или задача теории статистических решений (проверки гипотез).
Сформулируем и представим графически задачу приема в условиях помех.
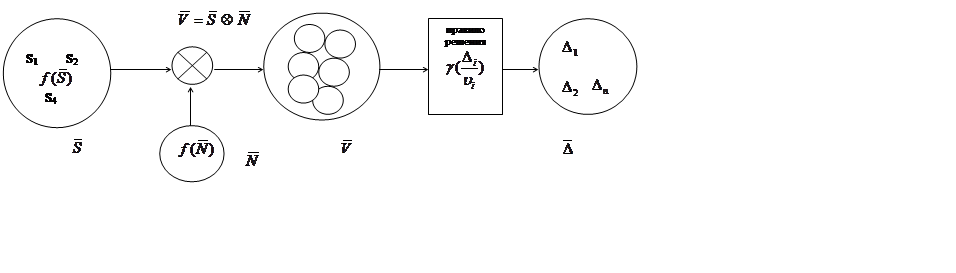 |
Существует множество (дискретное) сигналов ![]() с заданной вероятностной мерой
с заданной вероятностной мерой ![]() .
.
В канале связи сигналы из множества ![]() взаимодействуют с шумом так, что на
выходе канала имеем
взаимодействуют с шумом так, что на
выходе канала имеем ![]() . Считаем, что нам известны
вероятностные характеристики шума
. Считаем, что нам известны
вероятностные характеристики шума ![]() и способ
взаимодействия сигнала с шумом (аддитивный, мультипликативный).
и способ
взаимодействия сигнала с шумом (аддитивный, мультипликативный).
На приемном конце, таким образом, мы имеем дело с
пространством наблюдаемых значений ![]() (непрерывным),
каждая точка которого есть результат взаимодействия сигнала с шумом
(непрерывным),
каждая точка которого есть результат взаимодействия сигнала с шумом ![]() .
.
По результату наблюдения ![]() необходимо
вынести решение согласно некоторого правила
необходимо
вынести решение согласно некоторого правила ![]() ,
о том какой сигнал передавался.
,
о том какой сигнал передавался.
Множество решений ![]() дискретно
и обычно соответствует множеству сигналов (если нет стирания). Как видно из постановки,
на языке математической статистики задача приема сигналов есть задача проверки
гипотез.
дискретно
и обычно соответствует множеству сигналов (если нет стирания). Как видно из постановки,
на языке математической статистики задача приема сигналов есть задача проверки
гипотез.
Если использовать нерандомизированное правило
решений, то необходимо пространство ![]() разбить на
подмножества
разбить на
подмножества ![]() . Попадание в
. Попадание в ![]() точки
точки ![]() влечет
за собой решение
влечет
за собой решение ![]() о том, что передавался
сигнал
о том, что передавался
сигнал ![]() .
.
Пусть сигналов всего два ![]() и
и
![]() . Можно составить таблицу решений и
матрицу ошибок.
. Можно составить таблицу решений и
матрицу ошибок.
|
Передан сигнал |
Принято решение |
Комментарий |
|||
|
|
|
|
|
||
|
|
|
|
верное решение |
ошибочное решение о сигнале 1 |
|
|
|
|
|
ошибочное решение о сигнале 2 |
верное решение |
|
![]() - вероятность
ошибки первого рода (пропуск цели, риск заказчика, уровень значимости),
- вероятность
ошибки первого рода (пропуск цели, риск заказчика, уровень значимости),
![]() - вероятность
ошибки второго рода (ложная тревога, риск изготовителя),
- вероятность
ошибки второго рода (ложная тревога, риск изготовителя),
![]() - мощность
критерия,
- мощность
критерия,
![]() - оперативная
характеристика.
- оперативная
характеристика.
Чтобы вычислить вероятности ошибок надо знать
условные вероятности ![]() и
и ![]() .
.
Тогда, 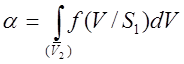
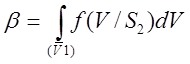 .
.
Принимая ошибочное решение, мы несем потери. В общем случае можно считать заданной матрицу потерь
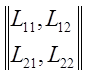 .
.
Решение, которое минимизирует среднюю величину потерь, или средний риск, называется байесовским. Чтобы найти его запишем выражение для среднего риска:
![]() .
.
Т.к. ![]() не зависит от
правила решения, необходимо минимизировать функционал:
не зависит от
правила решения, необходимо минимизировать функционал:
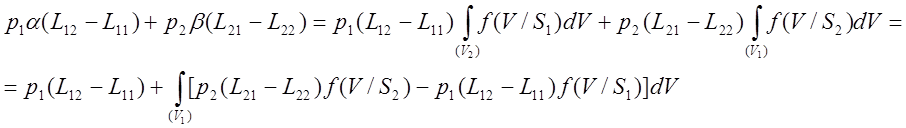
Минимум данного функционала достигается в том
случае, когда область ![]() выбирается так, что
подынтегральное выражение содержит все отрицательные и только отрицательные
значения, т.е.
выбирается так, что
подынтегральное выражение содержит все отрицательные и только отрицательные
значения, т.е.
![]() .
.
Таким образом, надо для принятия решения вычислить отношение правдоподобия:
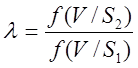 и сравнить с
величиной
и сравнить с
величиной 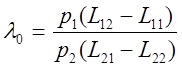 .
.
Если ![]() , выносится
решение о передаче сигнала
, выносится
решение о передаче сигнала ![]() ; если
; если ![]() , выносится решение о передаче
сигнала
, выносится решение о передаче
сигнала ![]() .
.
Для задач связи обычно ![]() -
верные решения потерь не дают;
-
верные решения потерь не дают; ![]() - ошибочные
решения вызывают равные потери, сигналы равновероятны
- ошибочные
решения вызывают равные потери, сигналы равновероятны ![]() .
В этом случае
.
В этом случае ![]() . Решение выносится в
пользу той гипотезы, которая более правдоподобна. Критерий минимального риска в
этом случае называется критерием максимального правдоподобия Фишера.
. Решение выносится в
пользу той гипотезы, которая более правдоподобна. Критерий минимального риска в
этом случае называется критерием максимального правдоподобия Фишера.
Если потери от ошибочных решений одинаковы, но ![]() , критерий минимального риска
переходит в критерий идеального наблюдателя Зигерта-Котельникова.
Гиперплоскость, разделяющая области
, критерий минимального риска
переходит в критерий идеального наблюдателя Зигерта-Котельникова.
Гиперплоскость, разделяющая области ![]() и
и ![]() будет иметь вид:
будет иметь вид:
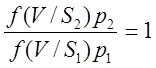 .
.
Отношение в левой части носит название обобщенного отношения правдоподобия. Если воспользоваться формулой Байеса, то можно записать это отношение как отношение апостериорных вероятностей гипотез:
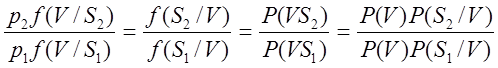 .
.
При использовании критерия идеального наблюдателя минимизируется величина ошибки.
![]() .
.
Для одномерного случая геометрически можно проиллюстрировать сказанное рисунком.
 |
Точка ![]() делит ось
делит ось ![]() на две области
на две области ![]() и
и ![]() .
Если наблюдаемый сигнал окажется в
.
Если наблюдаемый сигнал окажется в ![]() , выносится
решение о передаче
, выносится
решение о передаче ![]() , в
, в ![]() -
о передаче
-
о передаче ![]() . Суммарная ошибка равна
заштрихованной площади. Смещение
. Суммарная ошибка равна
заштрихованной площади. Смещение ![]() вправо или влево
может только увеличить ошибку.
вправо или влево
может только увеличить ошибку.
Таким образом. существует способ приема, при котором
величина ошибки распознавания сигналов минимальна. Этот способ и реализующий
его приемник называют оптимальным или идеальным. Вычислить ошибку и построить
схему можно, зная ![]() и
и ![]() .
Эта задача была решена Котельниковым.
.
Эта задача была решена Котельниковым.
Помехоустойчивость это способность системы правильно воспринимать сигналы, несмотря на искажения их и наличие непредсказуемых помех. Для дискретных сигналов помехоустойчивость можно оценить или измерить через вероятность правильного приема. Предельно достижимую в заданных условиях приема помехоустойчивость называют потенциальной помехоустойчивостью. Вопросы анализа помехоустойчивости различных систем передачи информации являются предметом теории потенциальной помехоустойчивости, которая была разработана Котельниковым в 1946 году. В частности, им была решена задача при следующих ограничениях:
1. Сигнал и
шум аддитивны ![]()
2. Закон
распределения шума в канале нормальный 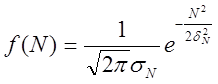
3. Шум в
канале белый, т.е. отсчеты некоррелированы и ![]()
4. На
приемном конце имеется полная информация о сигналах ![]() и
и
![]() вплоть до момента их существования
вплоть до момента их существования ![]()
В силу аддитивности и взаимной независимости
сигналов и помех для любого момента времени ![]() ,
лежащего на интервале
,
лежащего на интервале ![]() условный закон
распределения шума при наличии сигнала
условный закон
распределения шума при наличии сигнала ![]() будет
иметь вид:
будет
иметь вид:
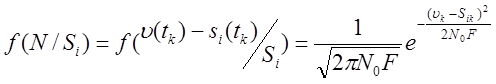 .
.
Отношение правдоподобия, следовательно, будет для
момента ![]() иметь вид:
иметь вид:
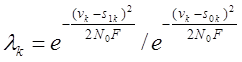 .
.
На интервале ![]() ,
если сигналы ограничены по спектру, можно взять
,
если сигналы ограничены по спектру, можно взять ![]() независимых
отсчетов.
независимых
отсчетов.
Тогда по совокупности отсчетов имеем:
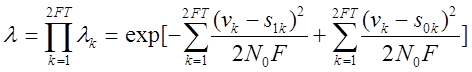 .
.
Если 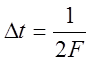 , то устреми
, то устреми ![]() для белого шума получим в пределе:
для белого шума получим в пределе:
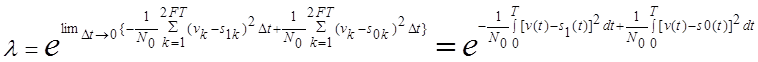 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.