Если в качестве критерия приема выбрать критерий
максимального правдоподобия Фишера, решение принимается сравнением ![]() с 1. Но это равносильно сравнению
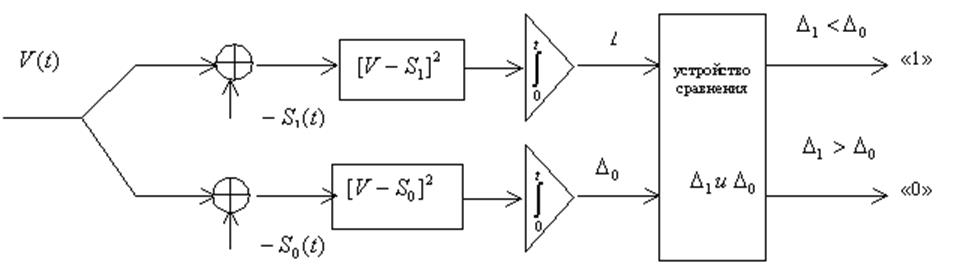
показателя у экспоненты с нулем. Получаем, следовательно, такую структурную
схему приемника, принимающего решения по наблюдаемым реализациям сигналов с
помехами:
с 1. Но это равносильно сравнению
показателя у экспоненты с нулем. Получаем, следовательно, такую структурную
схему приемника, принимающего решения по наблюдаемым реализациям сигналов с
помехами:
 |
Сравниваемые интегралы можно преобразовать, тогда получим другие варианты возможных реализаций оптимальных приемников.
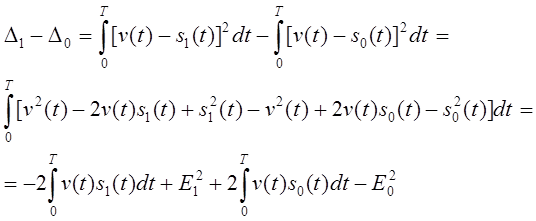
Сравнивать надо как следует из последнего выражения
(![]() и
и ![]() -
энергия сигналов единицы и нуля).
-
энергия сигналов единицы и нуля).
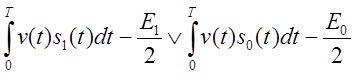 .
.
Здесь Е0 – энергия сигнала «0», Е1 – энергия сигнала «1».
Корреляционный приемник для этого варианта следующий:
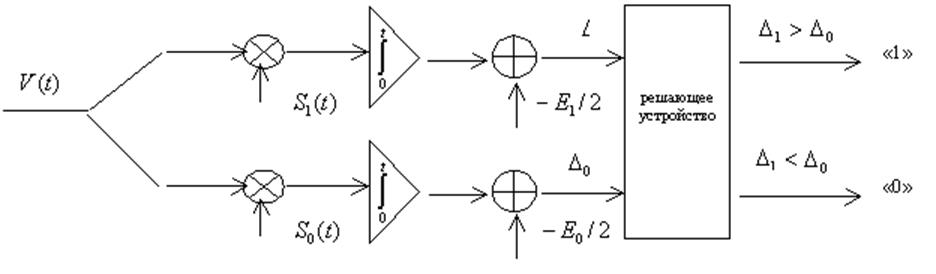 |
Если энергии сигналов равны, схема упрощается и приобретается весьма ценное свойство – нечувствительность к уровню входного сигнала.
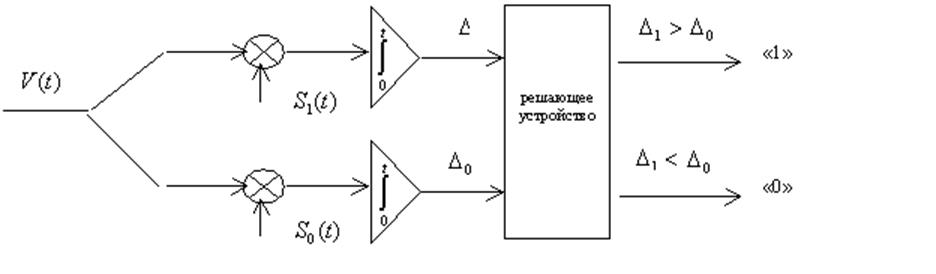 |
Реакция фильтра на входное воздействие ![]() может быть найдена как интеграл
свертки
может быть найдена как интеграл
свертки 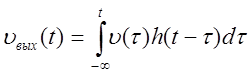 .
.
Подберем такой фильтр, чтобы к моменту ![]() его выходная реакция была равна
величине интеграла
его выходная реакция была равна
величине интеграла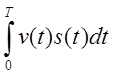 . Если сигнал поступит на
вход в момент
. Если сигнал поступит на
вход в момент ![]() , то должно быть
, то должно быть ![]()
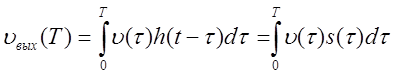 .
.
Отсюда ![]() , обозначим
, обозначим ![]() , получим
, получим ![]() .
.
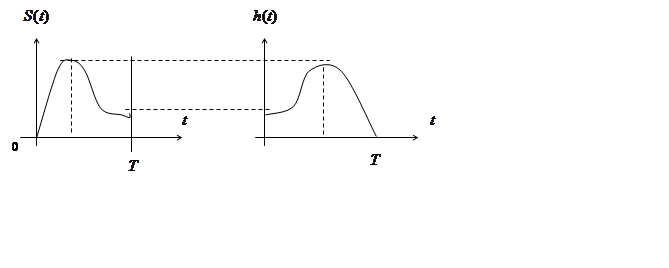 Фильтр,
импульсная переходная функция которого удовлетворяет последнему условию,
называют согласованным с сигналом. График для
Фильтр,
импульсная переходная функция которого удовлетворяет последнему условию,
называют согласованным с сигналом. График для ![]() является
зеркальным отображением сигнала
является
зеркальным отображением сигнала ![]() , когда зеркало
помещено в точку
, когда зеркало
помещено в точку ![]() и отсчет начинается от
плоскости зеркала.
и отсчет начинается от
плоскости зеркала.
Найдем комплексный коэффициент согласованного фильтра.
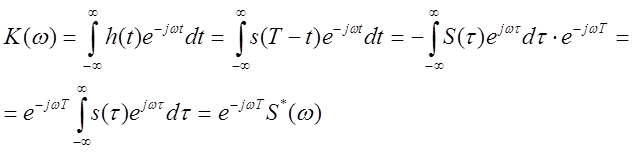
С точностью до амплитудного множителя и постоянной задержки передаточная функция согласованного фильтра является комплексно-сопряженной со спектром сигнала.
![]() .
.
Найдем выходной сигнал согласованного фильтра:
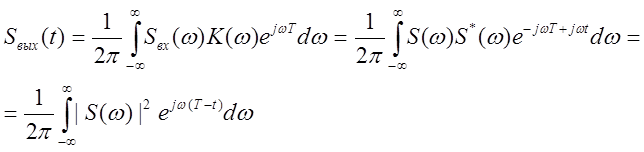
В соответствии с теоремой Релея при ![]() выходной сигнал равен:
выходной сигнал равен:
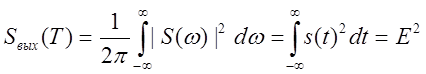 ,
,
т.е. все спектральные составляющие выходного сигнала
совпадают по фазе и в сумме дают максимальное значение ![]() ,
равное энергии сигнала. Во все остальные моменты времени фазы спектральных
составляющих различны и пика амплитуды сигнала не будет.
,
равное энергии сигнала. Во все остальные моменты времени фазы спектральных
составляющих различны и пика амплитуды сигнала не будет.
Функциональная схема приемника на согласованных фильтрах будет следующей:
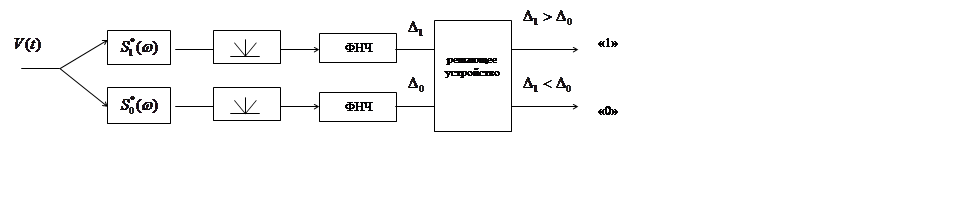
Выясним, с какой целью в последней схеме введен
детектор огибающей. Для этого получим формулу для выходного сигнала как функцию
времени. Пусть, например, входной сигнал ![]() ,
,
![]() , шум отсутствует.
, шум отсутствует.
Для корреляционного приемника:
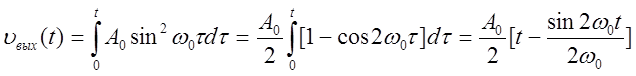
Для оптимального согласованного фильтра ![]() , будем полагать
, будем полагать ![]() выбранным так, что
выбранным так, что ![]() , т.е. на интервале
, т.е. на интервале ![]() укладывается целое число периодов
опорной частоты. Тогда
укладывается целое число периодов
опорной частоты. Тогда ![]() .
.
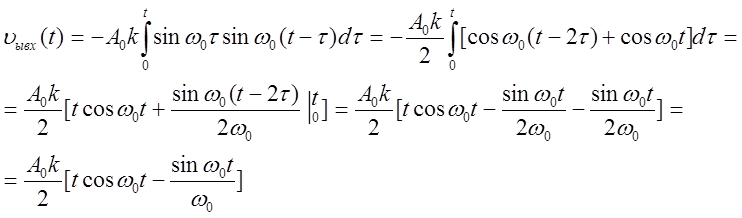
Графики процесса накопления будут:
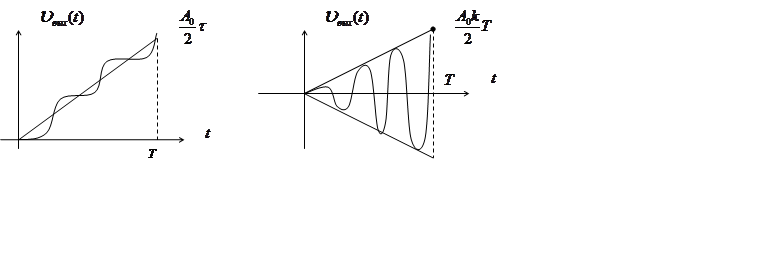 |
Пусть передан первый из сигналов, т.е. ![]() .
.
Решение ![]() , в данном случае
ошибочное, будет принято, если величина
, в данном случае
ошибочное, будет принято, если величина ![]() окажется
больше величины
окажется
больше величины ![]() .
.
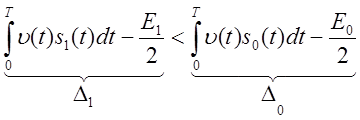 или
или
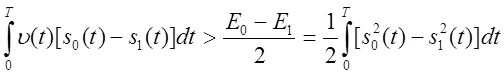 .
.
Искомая вероятность ошибки равна:
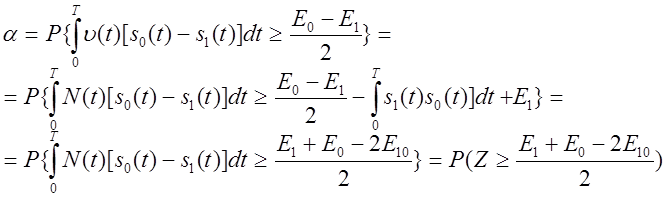
где 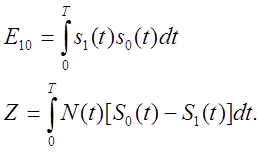
Величина ![]() имеет гауссовское
распределение, т.к.
имеет гауссовское
распределение, т.к. ![]() - подчинено гауссовскому
распределению и известно, что линейные преобразования гауссовских распределений
есть тоже гауссовское распределение.
- подчинено гауссовскому
распределению и известно, что линейные преобразования гауссовских распределений
есть тоже гауссовское распределение.
Найдем параметры распределения величины ![]() .
.
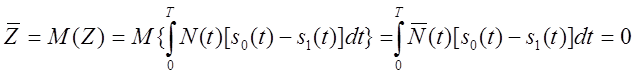
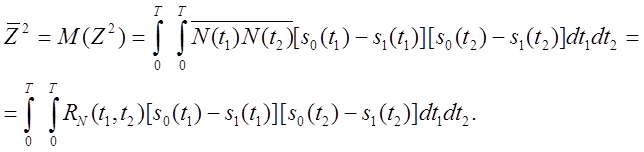
Поскольку шум белый, то 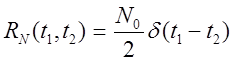 .
.
Тогда:
![]()
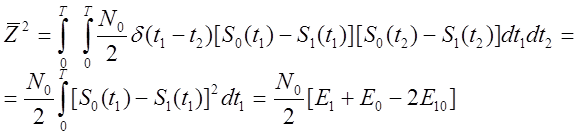
![]()
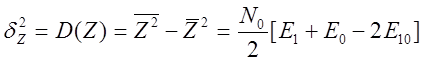
Получаем, следовательно:
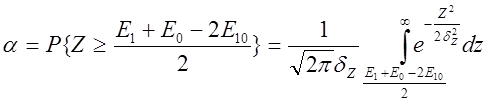
![]() .
.
Делаем замену переменной 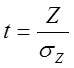 .
.
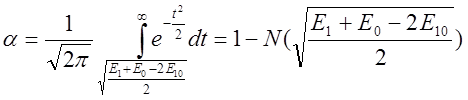
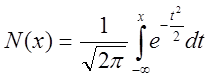 - функция
нормального распределения табулирована.
- функция
нормального распределения табулирована.
Аналогично, можно показать, что 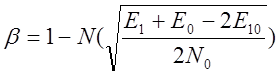 и средняя вероятность ошибки:
и средняя вероятность ошибки:
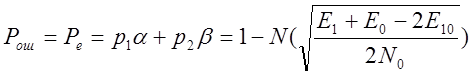 .
.
Если вспомним определение расстояния между сигналами в Гильбертовском пространстве:
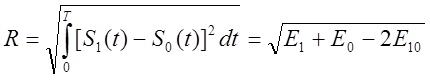 , то формулу для
вероятности ошибки можно переписать в таком виде:
, то формулу для
вероятности ошибки можно переписать в таком виде:
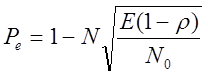 , где
, где
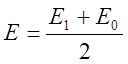 - средняя
энергия сигналов,
- средняя
энергия сигналов,
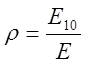 - мера несхожести
сигналов (при
- мера несхожести
сигналов (при ![]() совпадает с коэффициентом
корреляции между сигналами).
совпадает с коэффициентом
корреляции между сигналами).
Рассмотрим примеры.
1. Если бы
сигналы были неразличимые, то ![]() ,
, ![]()
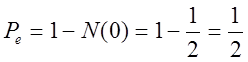 - очевидный
результат.
- очевидный
результат.
2. Пусть
сигналы противоположны, т.е. ![]() . Этот случай
соответствует двоичной фазовой модуляции со скачком фазы равным
. Этот случай
соответствует двоичной фазовой модуляции со скачком фазы равным ![]() .
.
![]() ,
, ![]()
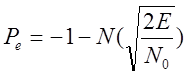
3. Пусть
сигналы ![]() и
и ![]() ортогональны.
Этот случай соответствует частотной модуляции в частности.
ортогональны.
Этот случай соответствует частотной модуляции в частности.
![]() ,
, ![]()
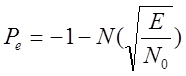
4. Для случая амплитудной модуляции:
![]() ,
, ![]() ,
, ![]() ,
,
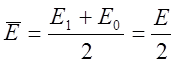
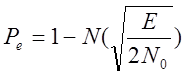 .
.
Как видно из формул, потенциальная помехоустойчивость определяется отношением энергии сигнала к спектральной мощности помех и видом (геометрией) сигналов. Максимальной помехоустойчивостью обладает система передачи с ФМ. Для получения одинаковой вероятности ошибки при использовании ортогональных сигналов требуется в два раза большая энергия, а при АМ в четыре раза большая, чем при ФМ.
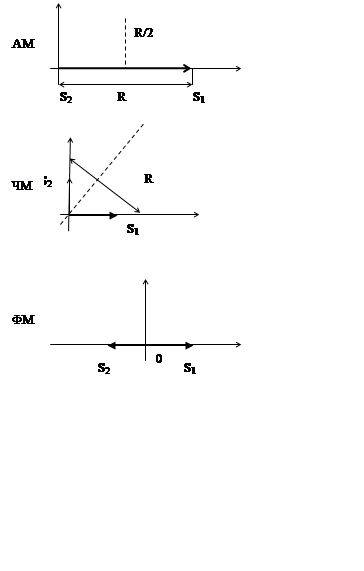
График зависимости вероятности ошибки от отношения 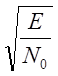 для ФМ, ЧМ и АМ сигналов приведен
ниже. На рисунке показано, как выбирается разделяющая граница, и как изменяется
в зависимости от вида сигналов расстояние между ними.
для ФМ, ЧМ и АМ сигналов приведен
ниже. На рисунке показано, как выбирается разделяющая граница, и как изменяется
в зависимости от вида сигналов расстояние между ними.
 |
|
1 |
1 |
2 |
3 |
4 |
|
|||
|
|
10-1 |
|||||||
|
10-2 |
||||||||
|
10-3 |
||||||||
|
10-4 |
||||||||
|
10-5 |
||||||||
|
Ре |
В этом случае ![]() -
единственной колебание
-
единственной колебание ![]() любой формы. Векторы
сигналов
любой формы. Векторы
сигналов ![]() и
и ![]() выбираются
так, что
выбираются
так, что ![]() и
и ![]() .
.
Тогда ![]()
![]()
![]() .
.
Противоположными являются два сигнала любой формы, отличающиеся знаком.
В этом случае ![]() ,
,
![]() и
и ![]() -
ортонормированные колебания. Векторы сигналов выбираются так:
-
ортонормированные колебания. Векторы сигналов выбираются так:
![]()
![]() .
.
Временные графики сигналов ![]() и
и
![]() зависят от вида ортонормального
набора.
зависят от вида ортонормального
набора.
Так, если
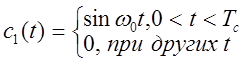
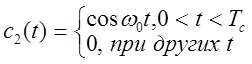
![]()
![]() .
.
В этом случае образуется М сигналов из ![]() - ортогональных колебаний
- ортогональных колебаний ![]() с конфигурацией векторов:
с конфигурацией векторов:
![]()
![]()
![]() .
.
Временные графики сигналов определяются набором ортонормальных колебаний. Например, можно взять
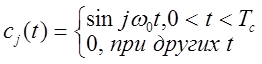
Тогда ![]() - сигналы
являются отрезками гармонических колебаний кратных частот
- сигналы
являются отрезками гармонических колебаний кратных частот ![]() . Реализовывать технически такой
набор не очень удобно.
. Реализовывать технически такой
набор не очень удобно.
В этом случае из ![]() ортогональных
колебаний
ортогональных
колебаний ![]() образуется
образуется ![]() сигналов
путем добавления к каждому из ортогональных сигналов противоположного сигнала.
сигналов
путем добавления к каждому из ортогональных сигналов противоположного сигнала.
Например, к векторам сигналов из п.2 ![]() и
и ![]() добавляются
добавляются
![]() - противоположный
- противоположный ![]() и
и ![]() -
противоположный
-
противоположный ![]() .
.
В этом
случае из ![]() колебаний (ортогональных)
образуется
колебаний (ортогональных)
образуется ![]() сигналов. Конфигурация векторов
сигналов выбирается так, что они соответствуют вершинам
сигналов. Конфигурация векторов
сигналов выбирается так, что они соответствуют вершинам ![]() -мерного
куба. Так при
-мерного
куба. Так при ![]() :
:
![]()
![]()
![]()
![]()
![]() - постоянная
величина.
- постоянная
величина.
Это набор сигналов равноудаленных и предельно
удаленных друг от друга при заданной энергии сигналов. В этом случае ![]() . Симплексные сигналы можно получить
из ортогональных, если зафиксировать расстояние между сигналами
. Симплексные сигналы можно получить
из ортогональных, если зафиксировать расстояние между сигналами ![]() .
.
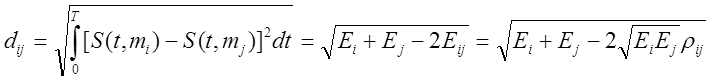
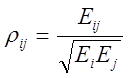 - коэффициент
взаимной корреляции сигналов.
- коэффициент
взаимной корреляции сигналов.
Расстояние между сигналами не изменится, если ко
всем ![]() добавить одно и то же колебание
добавить одно и то же колебание ![]() . На этом и основан переход к
симплексным сигналам. Если найти минимум суммарной энергии вновь образованных
сигналов:
. На этом и основан переход к
симплексным сигналам. Если найти минимум суммарной энергии вновь образованных
сигналов:
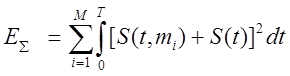
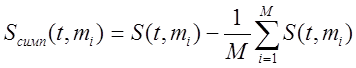
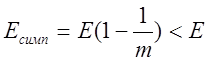
![]() - энергия
ортогонального сигнала.
- энергия
ортогонального сигнала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.