Декодер Питерсона-Горенстейна-Цирлера

6.9  Декодер Питерсона-Горенстейна-Цирлера

Пусть , где - величина l-ой ошибки.

Реально мы не знаем ни р, ни номеров сбытых символов , ни значений . Легко находятся компоненты синдрома

Введем более компактные обозначения - величины ошибок

 - локатор -ой ошибки – элемент поля ассоциированный с положением ошибки на позиции .

Тогда,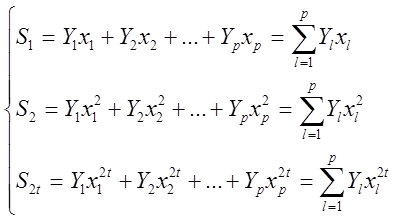

Система имеет единственное решение. Любой метод решения этой нелинейной системы – алгоритм декодирования. Питерсон изложил искусственный прием ее решения, состоящий в следующем. Введем промежуточные переменные , которые могут быть вычислены по компонентам синдрома , а по ним положение ошибок.

                                             (*)

.

Корнями этого многочлена (локатора ошибок) являются элементы ,  - обратные к локаторам ошибок. Знаем корни – знаем номера сбитых символов.

Умножим обе части равенства (*) на  и положим . Тогда левая часть (*) будет нулем и получим:

.

Просуммируем по  от 1 до , тогда для каждого  получим уравнение

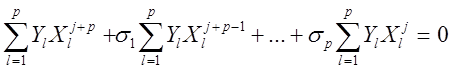
Каждая сумма слева компонента синдрома.

.

Получается система линейных уравнений.

, .

В матричном виде эта система имеет вид:

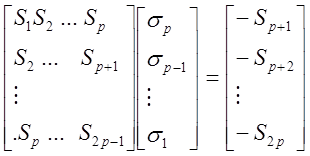
Доказано, что матрица невырождена, если произошло ровно р ошибок.

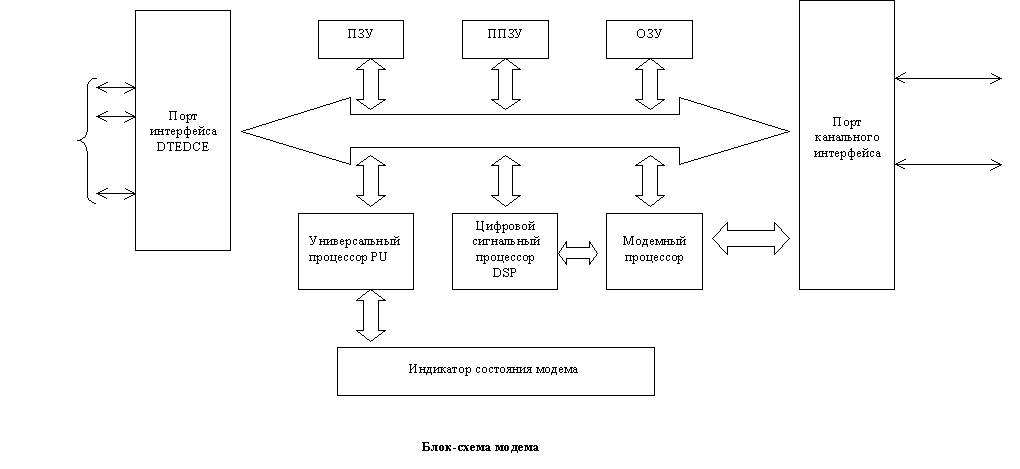
Блок схема алгоритма декодирования приведена ниже.

 

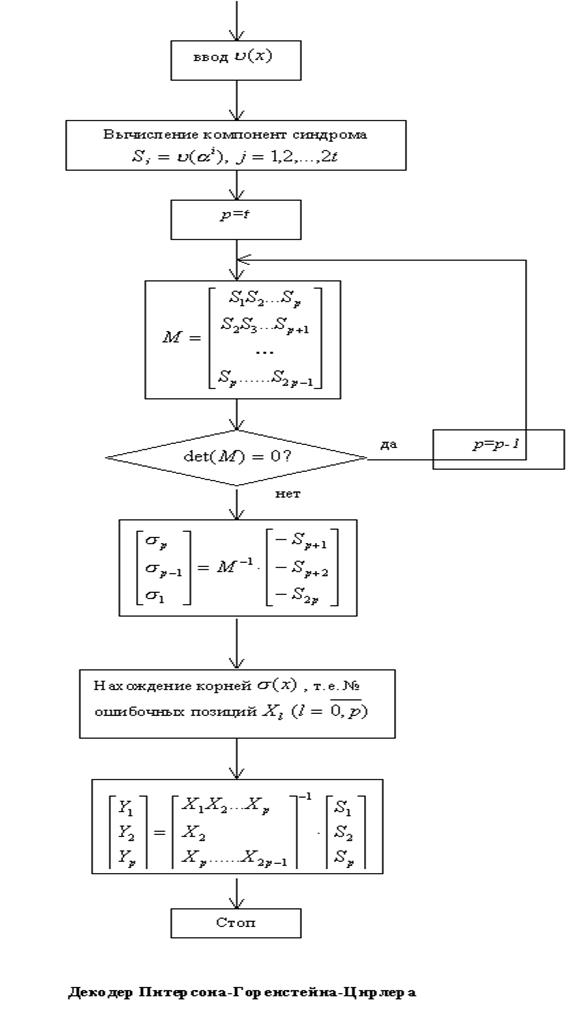Нахождение корней, поскольку они являются элементами поля  легко осуществляется путем перебора, известного под названием процедура Ченя. Сама схема вычисления значения  при  наиболее экономичной по числу операций будет схемой Горнера:

.

Рассмотрим два примера. Первый вариант для кода БЧХ  , , .

Пусть при декодировании (на входе) имеет место исправляемая комбинация ошибок. Принято из канала .

Убедитесь, что декодер Питерсона-Горенстейна-Цирмера правильно декодирует информацию. Получите конкретно, что передавалось по каналу и какой вектор ошибок.

Шаг 1

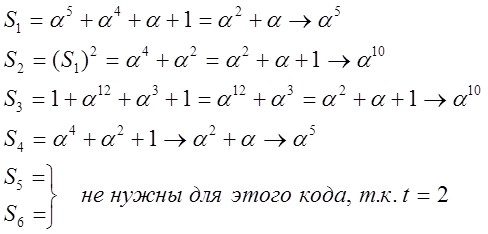
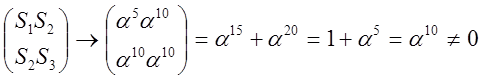
Вывод: 2 ошибки.

Шаг 2

Находим коэффициенты системы уравнений и, решая ее, коэффициенты локатора ошибок.

Шаг 3

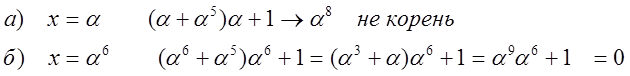
Позиция №9 кода ошибочная .

Позиция № 6 кода ошибочная.

Результат декодирования:

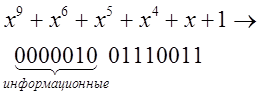
передана цифра 2. В канале 2 ошибки .