Помехоустойчивое кодирование, страница 6

Кодирование проще выполнять систематическим кодом. В этом случае необходимо вычислить значения  проверочных символов. Каждый проверочный символ согласно алгоритму кодирования (матричное умноже­ние) есть сумма по модулю два самое большее  информационных симво­лов. Следовательно, число двоичных сумматоров в схеме кодера будет не больше . Для согласования скоростей приема безизбыточных данных от источника и передачи закодированного сообщения в канал мо­жет потребоваться входной и выходной буферы из  и  ячеек памяти. Общая сложность , где  - скорость кода.

Сложность декодера в первую очередь зависит от того, обнаруживаем мы ошибки или исправляем, является декодер полным или неполным. Декодирование по максимуму правдоподобия называют еще декодировани­ем по манизму расстояния. Принятая комбинация сравнивается по мет­рике Хэмминга с каждой из кодовых и выбирается как решение та кодо­вая комбинация, к которой ближе всего принятая последовательность. Значит, потребуются  - разрядных схем сравнения, буферные регистры и память для кодовых слов. Общая сложность составит , т.е. растет по экспоненте в зависимости от числа информационных разрядов. В неполном декодере пре­дусматриваются сравнение полученного наименьшего расстояния со зна­чением кодового расстояния, и отказ от декодирования, если это рас­стояние больше .

При синдромном декодировании на вычисление синдрома потребуется не более  сумматоров и для полного декодера необходима память лидеров смежных классов (вариантов направляемых ошибок) на  -разрядных слов. Общая сложность будет составлять , т.е. сложность синдромного декодера растет по экспоненте в зависимости от числа избыточных символов. Если ошиб­ки только обнаруживать, сложность декодера будет определяться схемой вычисления синдрома .

Относительно синдромного декодирования надо сделать два замечания. Во-первых, не обязательно в качества лидеров смежных классов надо брать векторы наименьшего веса. Вместо хэммингового расстояния в канале с пакетированием надо использовать комбинаторную метрику, т.е. исправлять наиболее вероятные варианты ошибок - пакеты. Во-вторых, не обязательно в памяти хранить все варианты ошибок, можно ис­пользовать математическую структуру кода (например, цикличность).

6.4.4  Мажоритарное декодирование.

Основная идея, лежащая в основе алгоритма, заключается в том, что информационные символы могут быть вычислены через канальные символы разными способами. Решение выносится голосованием по большинству. Требуется, однако, выполнение некоторых условий к проверочным соотношениям. Это означает, что не любой код допускает мажоритарный вариант декодирования. Рассмотрим код с . Его проверочная матрица:

Проверочные соотношения, определяющие синдром, будут следующими:  или .

                                              

                                              

                                            

                                            

Поскольку, если нет ошибок, все , то и комбинации . Система проверок  называется разделенной относительно последнего  символа. Он входит во все проверочные соотношения, каждый другой символ только в одно. Если произошла одна ошибка в позиции , то получим . Если одна ошибка в любой другой позиции получим три единицы и ноль. Значит, ошибку в 14 позиции исправим по правилу: если 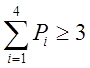, то , иначе .

Любая комбинация из двух ошибок, не содержащая , приведет к нарушению не более двух уравнений, а содержащая  не менее трех. Значит можно по тому же правилу исправлять и все двойные ошибки. Рассматривается циклический код, поэтому ошибки в остальных позициях тоже исправляются по четырем соотношениям  после циклического сдвига.

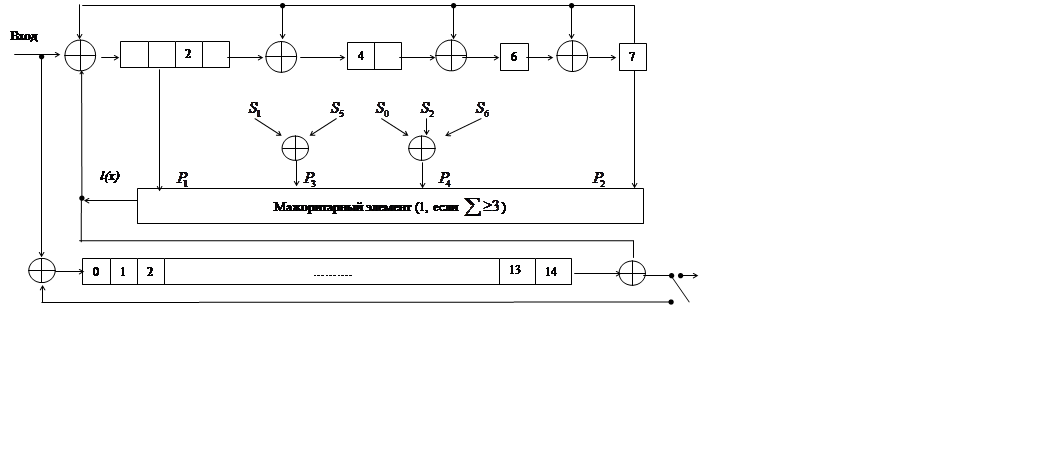
Рассмотренный код является кодом с одношаговым разделением. Более общий случай  - -шаговое разделение. Основное достоинство алгоритма мажоритарного декодирования – простота. Если нужна высокая скорость и умеренный выигрыш от кодирования, то надо применять этот алгоритм. Ниже приведена схема декодера - кода.

 

6.5  Циклические коды. Необходимое и достаточное условие цикличности.

Циклический код является частным случаем линейного кода, когда любая циклически сдвинутая кодовая комбинация является также кодовой комбинацией. Непосредственная проверка выполнения этого условия для линейных кодов представляющих практический интерес неосуществима, т.к. велика мощность кода: , где - основание кода, - число информационных символов (). К циклическому коду можно прийти как к частному случаю другого кода – полиномиального. Полиномиальный код задается наиболее просто образующим многочленом , степени , - длина кодовой комбинации. Множество многочленов степени меньшей  делящихся на  является множеством кодовых комбинаций. Полиномиальный код это тот же линейный код только иначе представленный. Вместо -символьных последовательностей (векторов) их многочленная запись по формальной измененной . Формальная переменная используется по сути для указания номера позиции в -разрядной комбинации, где имеется ненулевой символ. В пользу перехода к многочленному представлению можно указать по крайней мере три аргумента:

-  при  в среднем на 50% «экономится»  длина записи;

-  появляется более простая процедура выбора подпространства (т.е. кода), вместо базисных векторов можно использовать образующий многочлен;

-  упрощается процедура кодирования, вместо матричного умножения, умножение (или деление) многочленов.

Найдем необходимые и достаточные условия цикличности полиномиального кода. Пусть  - кодовый вектор, его многочленная запись . Циклически сдвинутый вектор , его многочленная запись .