Помехоустойчивое кодирование, страница 4

-  множество абелева группа по сложению;

-  выполняется дистрибутивный закон для векторов, т.е. , ;

-  выполняется дистрибутивный закон для скаляров, т.е. , ;

-  выполняется ассоциативный закон, т.е. , .

Линейное пространство может быть задано базисными векторами. Это такие  линейно независимых векторов, которые позволяют любой вектор пространства  выразить в виде . Минимально возможное число (п) линейно-независимых векторов есть размерность пространства.

Скалярным произведением векторов называется скаляр, определяемый по правилу . Если , то такие вектора ортогональны.

Множество всех векторов пространства , ортогональных пространству , образует подпространство , которое называют нулевым для .

Если некоторый вектор ортогонален базисным векторам , то он принадлежит . Если имеет размерность , подпространство  размерность , то размерность  равна .

6.4.2  Задание линейных кодов

Пусть - линейное  -мерное пространство над полем . Линейным блоковым -м кодом размерности  длины  называется вся­кое -мерное подпространство  пространства . Для обозначения линейного кода используется символ -код.

Встречается другое название линейного кода (групповой код), которое связано с понятием группы. Двоичный код называют групповым, если сумма двух любых его кодовых слов есть снова кодовое слово. Это есть следствие из свойств группы.

Существует несколько способов задания линейных кодов. В зави­симости от целей и задач оказывается удобным тот или иной способ представления.

1. Очевидно, что к линейно независимых векторов подпространства А, образующих его базис , позволяют выразить любой вектор этого пространства: ; , ,  - базисные векторы. Такой способ задания кода удобен для доказательства теорем, исследования свойств кода.

2. Если полученное соотношение записать в матричной форме

, , ,

где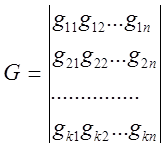

то придем ко второй форме задания линейного кода. Матрица G , строки которой есть k линейно независимых векторов кода (например, базис­ные векторы, представленные через свои компоненты), называется порождающей матрицей -кода. Набор  является информационным , . Набор  - за­кодированное информационное сообщение.

Ясно, что для любого -кода А существует не одна порож­дающая матрица, так как всякая матрица QG , где Q - невырожденная матрица размером , тоже является порождающей матрицей -ко­да.

За счет перенумерации координат и выбора образующих векторов всегда можно порождающую матрицу привести к каноническому виду , где Е – единичная матрица размера , а  В – произвольная матрица размера :

;

; ; ; .

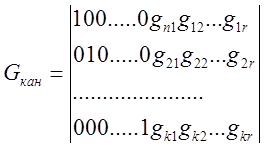Код, заданный канонической матрицей, является систематическим, т.е. проверочные и информационные символы разделены.

3. Задание кода с помощью проверочной матрицы .

Если задан код А как подпространство  пространства  размер­ности , то существует подпространство , ортогональное  (на­зываемое нулевым) размерности . Это подпространство дает тоже линейный код. Обозначим его . Он называется дуальным (двойст­венным) к А.

Обозначим через Н порождающую матрицу кода . Тогда код А можно определить как множество векторов  таких, что

                                                         (*)

Матрица Н называется проверочной матрицей -кода. Если, как и раньше, обозначить компоненты вектора  , элементы матрицы  - , , , то развернутая запись мат­ричного уравнения приведет к системе уравнений из  штук вида .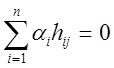

Это означает, что компоненты любого кодового слова удовлетворяют со­вокупности  линейных независимых однородных уравнений. Эти уравнения называется обобщенными проверками на четность. Для двоич­ного кода они представляет проверку на четность определенных групп информационных символов.

Так как уравнение (*) справедливо для всех слов кода, то оно справедливо и для строк порождающей матрицы  (базисных векторов). Следовательно, проверочная и порождающая матрицы кода связаны соот­ношением .

Всякая проверочная матрица -кода комбинаторно эквивалентна матрице, представленной в канонической форме:

, , , .

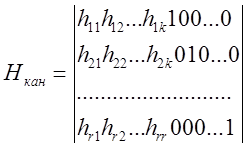
Связь между проверочной и порождающей матрицей устанавливается следующей теоремой.

Пусть  - порождающая матрица - кода, пред­ставленная в канонической  форме, т.е.  - единичная матрица разме­ра ; - матрица размера  с элементами из поля . Тогда матрица  - проверочная матрица -ко­да , представленная в канонической форме.

Задание кода проверочной матрицей удобно для осуществления де­кодирования.

4. Модулярное представление кода. Производящая матрица кода G может иметь разнообразие типов столбцов в   штук, так как в столб­це  символов и чисто нулевой столбец не имеет смысла. Если все типы столбцов записать в виде матрицы М размерности , то код можно задать, указав  положительных чисел , где  - число столбцов типа  в матрице G:

.

Это и есть модулярное задание кода.  дает в результате все ненулевые кодовые векторы. Важную роль играет матрица . Это симметричная матрица, содержащая по одному столбцу каждого типа.

Свойства линейных кодов

Так как расстояние между двумя векторами  и  равно весу суммарного вектора , а для линейного кода суммар­ный вектор тоже принадлежит коду, то кодовое расстояние равно мини­мальному весу множества кодовых векторов . Поскольку минимум  берется по всем векторам кода А отличным от нулевого, то для поиска кодового расстояния достаточно  сравнений. Для произ­вольного кода число сравнений равно     . По виду матрицы Н  можно судить о защитных свойствах кода, в частности, о значении ко­дового расстояния.

1. Теорема.   Если любые  столбцов матрицы  линейно независимы, то кодовое расстояние не меньше, чем .