Понятие передаточного числа вершины и медианы графовой модели сети. В-медианы

(Этот вариант сделан НиКо (группа ЗТ-44) только для узкого круга пользователей J).

4 вопрос: Понятие передаточного числа вершины и медианы графовой модели сети.В-медиа-ны. Практическое использование медиан при оптимизации проектных решений по сети электросвязи города.

Передаточное число вершины Хg в графе G равное Х*U есть численное значение функцио-нала:     , где  - это расстояние от  вершины  до верши-

ны ,       -   это вес вершины .

Медианой графа G называется такая вершина , у которой передаточное число минимально.

В проектировании понятие медиана и передаточное число применимы когда они имеют физичес-кий смысл: например если вес вершины обозначить как количество телефонных аппаратов на этой станции , а вес ребра принять как расстояние в километрах до этой станции от другой станции се-ти, то тогда найденное передаточное число тоже будет иметь конкретный физический смысл как сумма канало-километров  кабельных линий . Таким образом, подсчитывая передаточные значе-ния вершин (станций) и сравнивая их можно определить вершину для оптимального размещения АТС на сети , отсюда видно ,что определение оптимального места размещения отдельной АТС связано с медианой графа .

Если необходимо разместить несколько станций на сети , т.е. с минимальными затратами кабеля, то определяют уже b-медиану ,  где b – это количество станций .

Пример : Найти передаточное число для  всех вершин графа и определить медиану. 

                

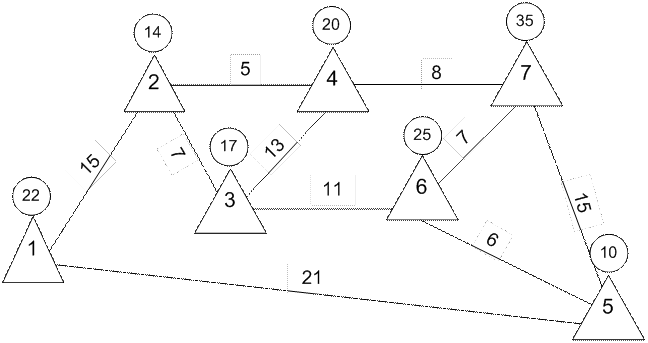
                                                      Рис.1  Заданный граф G .

Цифры в кружках – это условная емкость станции .

Произвольно выбираем станцию , пусть это будет вершина 5 , определяем её передаточное число :

             0*10 + 21*22 + 6*25 + 15*35 = 1137

Теперь находим передаточное число для трех смежных с ней вершин (это вершины 1, 6 и 7)

             0*22 + 15*14 + 21*5 = 525

             0*25 + 11*17 + 6*10 + 7*35 = 492

             0*35 + 8*20 + 7*25 + 15*10 = 485

Сравниваем значения их передаточных чисел и выбираем из них вершину с наименьшим переда-точным числом (это вершина 7). Так как значение  , то теперь определяем  передаточное

число для вершин смежных с вершиной 7 (это вершины 4, 5 и 6) :

             0*20 + 5*14 + 13*17 + 8*35 = 571

Передаточные числа вершин 5 и 6 уже были найдены ранее.

 Так как найденные передаточные числа больше чем сравниваемое значение вершины 7 , то на этом алгоритм поиска медианы заканчивается и вершина 7 является претендующей на медиану графа G.

Наименьшее передаточное число имеет вершина 7 – она  является медианой заданного графа G,

нотак как алгоритм приближенный, то нельзя утверждать что это точно медиана , потому что может найтись вершина с меньшим передаточным числом.

b-медианы.

 Задача оптимизации проектных решений в том, чтобы найти такое расположение проектируемых АТС , при котором суммарные затраты были бы минимальными. Критерием оптимальности распо-

ложения УВС (РАТС) является минимум суммы канало-километров – для аналоговых станций или

тракто-километров для цифровых станций проходящих через УВС (РАТС). Эта задача сводится к определению b-медианы на графовой модели сети.   

Приблизительный алгоритм нахождения b-медианы состоит из 6 шагов :

1) В графе G произвольно выбрать подмножество  и разбить множество вершин Х на «b» подмножество, таким образом . чтобы произвольная вершина  отнесена (прикреплена) к бли-

жайшей вершине Х.

2) Линейно упорядочить вновь образованные «b» подмножества , т.е. пронумеровать (1,2,3,…) их.

3) Рассмотреть упорядоченные на шаге 2 подмножества последовательно . в очередном подмно-жестве найти вершины смежные с некоторой вершиной  , определить передаточные числа

для каждой из этих вершин рассматривая соответствующую часть графа как самостоятельный граф .

4) Заменить вершину на вершину с меньшим передаточным числом . если такого нет, то перей-ти к следующему шагу 5, если есть – на шаг 6.

5) Для подмножества   определить значение функционала и запомнить.

6) Процедуры замены и вычисления начиная с 1 шага продолжать до тех пор, пока не произойдет увеличение от  , т.е. как только найдется увеличение от полного цикла , алгоритм закончится.