Алгоритм Прима-Краскала. Его применение при оптимизации проектных решений

     (Этот вариант сделан НиКо (группа ЗТ-44) только для узкого круга пользователей J).

2 вопрос:Алгоритм Прима-Краскала. Его применение при оптимизации проектных решений

Одной из важнейших задач , возникающих при проектировании сетей связи – определение кратчайших путей между всеми парами узлов сети. Предполагается что существует несколько вариантов путей соединяющих пару вершин, а выбран один из них – кратчайший по длине.

Для нахождения кратчайшей коммутационной сети используется алгоритм Прима-Краскала в двух существующих его разновидностях:

Первая разновидность алгоритма Прима-Краскала.

Шаг 1.  Упорядочить ребра графа G по убыванию их весов , то есть построить ориентировочный ряд,состоящий из весов ребер : первое ребро – с максимальным весом , последнее ребро – с минимальным. Если два или более ребер имеют одинаковые веса, они упорядочиваются произвольным образом.

Шаг 2.  Просматриваем последовательно все ребра начиная с ребра наибольшего веса.Определяем можно ли эти ребра удалить из графа не нарушив при этом его связности, т.е. определить есть ли ещё путь, не считая пути через удаляемое ребро, по которому можно пройти от одной до другой вершины заданного графа.

Оставшиеся ребра образуют минимальное остовное дерево данного графа G.

Пример :

Задана графовая модель сети G .

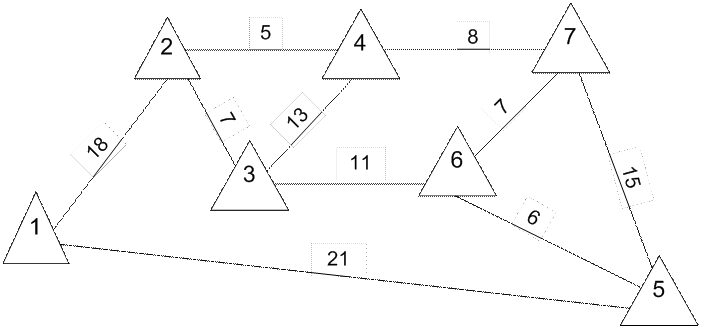
Рис.1  Граф G

Шаг 1.   21, 18, 15, 13, 11, 8, 7, 7, 6, 5.

Шаг 2.   Удаляем ребра согласно алгоритма и в результате получаем минимальное остовное дерево графа G.

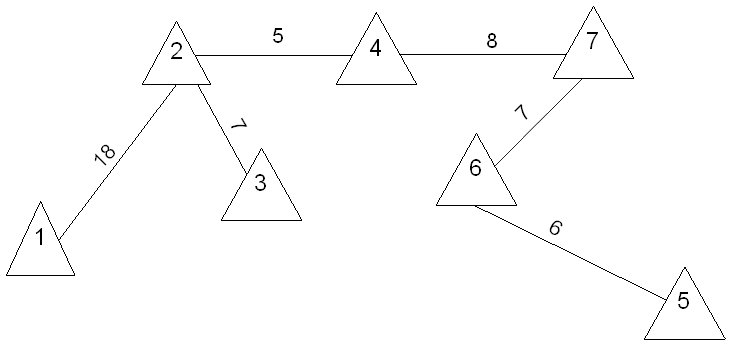
Полученное остовное дерево имеет минимальный суммарный вес ребер :                

Вторая разновидность алгоритма Прима-Краскала.

Состоит из двух шагов.

Шаг 1:   Упорядочить ребра графа по возрастанию веса ребер (построить некоторый численный ряд) .

Шаг 2 :    В соответствии с рядом построенным на первом шаге последовательно решить вопрос включить ли в будущее остовное дерево новое ребро. Первое ребро (минимальное) включается обязательно , следующие ребра включаются согласно правила: если при включении ребра может образоваться цикл, то ребро не включается в будущее дерево.

Пример:

Задана графовая модель сети связи G :

Шаг 1 :   5, 6, 7, 7, 8, 11, 13, 15, 18, 21

Шаг 2 :   Удаляем ребра согласно алгоритма и в результате получаем минимальное остовное дерево графа G.

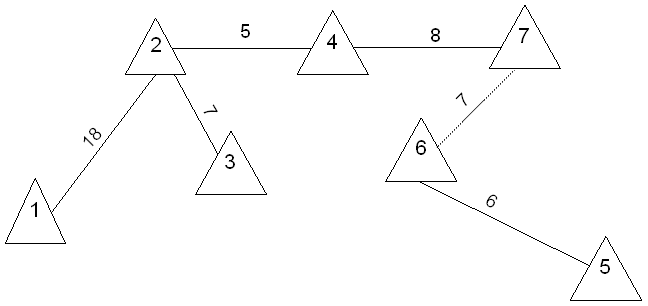
Полученное остовное дерево имеет минимальный суммарный вес ребер :