С учетом всего вышесказанного, в качестве усилителя сигнала, поступающего с выхода фотодетектора, выберем двухкаскадный усилитель с отрицательной обратной связью (ООС), схема которого при постоянном токе выглядит так, как показано на рисунке 2.2.
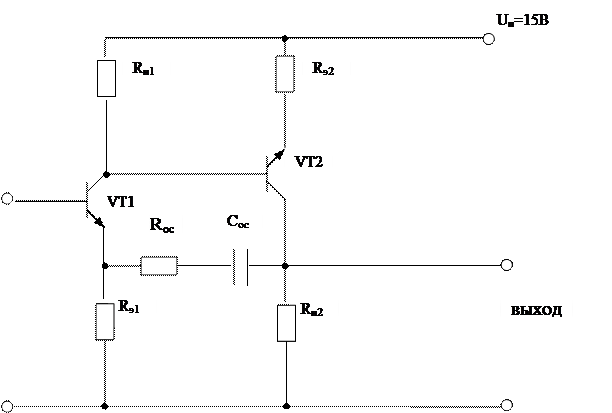 |
Рисунок 2.2 – Схема двухкаскадного усилителя с ООС при постоянном токе
Расчет режима по постоянному току
Произведем расчет данного
двухкаскадного усилителя при постоянном токе ![]() .
.
1) Зададим напряжение источника питания Uпит=15В и режимы каскадов Uкэ1=Uкэ2=5В, Iк1=Iк2= Iэ1=Iэ2 =5мА.
2) Рассчитаем
напряжение Uн2= Uпит - Uкэ2=15-5=10В, тогда 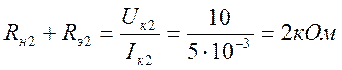
Распределяем суммарное сопротивление следующим образом:
Rэ2=300 Ом, а Rн2=1,7кОм.
3) Рассчитаем напряжение Uн1. Известно, что на коллекторе первого каскада подает больше половины напряжения Uпит, то есть Uн1=(0,4…0,5) Uпит. Для получения наибольшего коэффициента усиления сопротивление Rэ1 выбирается малым, так как его изменением в широких пределах не удается расширить полосу пропускания первого каскада из-за сильного шунтирования его большой величиной входной емкости. Поэтому примем Uн1=9,5В.
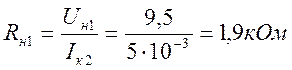
4) Напряжение на эмиттере первого каскада получим из соотношения:
Uэ1= Uпит - (Uкэ1+Uн1)=15-(5+9,5)=0,5В,
Тогда
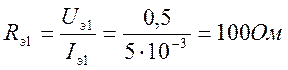
5) Определим емкость в цепи обратной связи:
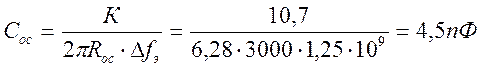
Эквивалентная схема данного двухкаскадного усилителя для переменного тока показана на рисунке 2.3.
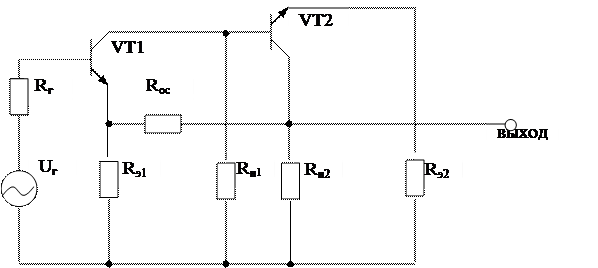 |
Рисунок 2.3 – Эквивалентная схема двухкаскадного усилителя с ООС при переменном токе
Будим считать, что первый
каскад нагружен на сопротивление Rн1 и входную проводимость второго каскада Yвх2, второй каскад – на сопротивление Rн2, параллельное соединение
коллекторного резистора Rк2 и
нагрузочного сопротивления Rн.
Паразитные емкости эмиттерных резисторов Rэ1 и Rэ2 не учитываем, так как они улучшают
частотные свойства каскадов![]() .
.
Рассчитаем данную схему,
если заданы глубина ООС ![]() =10, а коэффициент
усиления усилителя по постоянному току КБС=107.
=10, а коэффициент
усиления усилителя по постоянному току КБС=107.
КБС – коэффициент усиления усилителя без обратной связи,
γос – коэффициент передачи цепи обратной связи, определяемый как
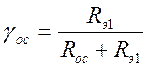 ,
(2.16)
,
(2.16)
1)Определяем γос:
так как ![]() , тогда
, тогда
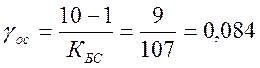 ,
(2.17)
,
(2.17)
2) Определяем коэффициент усиления “двойки” с ООС – К(jx) из выражения:
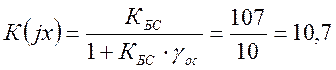 ,
(2.18)
,
(2.18)
3) Для получения наибольшего коэффициента усиления величина Rэ1 должна быть малой. По предыдущим расчетам имеем: Rэ1=100 Ом.
Величина ![]() . Проверим правильность выбора Rос из соотношения (2.19):
. Проверим правильность выбора Rос из соотношения (2.19):
![]() , (2.19)
, (2.19)
Выберем для выполнения всех условий Rос=3кОм, тогда с учетом полученных значений и выражения (2.16) получаем:
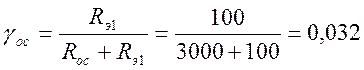
4) Оценим коэффициенты усиления для обоих каскадов.
а) Используя выражения для Y– параметров и коэффициента усиления по напряжению нагруженного четырехполюсника, записываем для первого каскада:
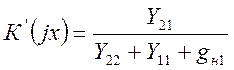 ,
(2.20)
,
(2.20)
Где gн1 – проводимость, вычисляемая как 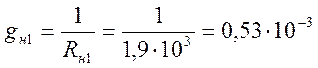
Подставляя полученные выражения для Y- параметров и величину проводимости gн1 в формулу (2.20) получаем, что
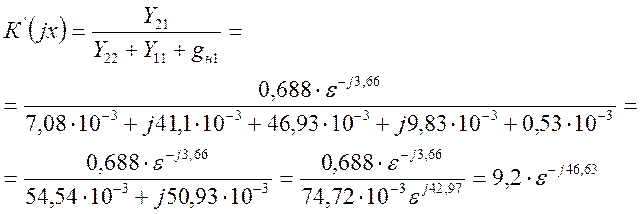
Определим коэффициент усиления по напряжению нагруженного четырехполюсника для первого каскада К1(jx) вторым способом:
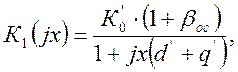 (2.21)
(2.21)
где ![]() - коэффициент нагрузки;
- коэффициент нагрузки;
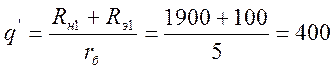 - коэффициент местной обратной связи;
- коэффициент местной обратной связи;
![]() - коэффициент местной обратной связи;
- коэффициент местной обратной связи;
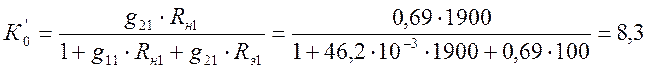 -
коэффициент усиления первого каскада на средних частотах.
-
коэффициент усиления первого каскада на средних частотах.
С учетом полученных значений имеем:
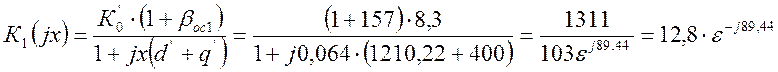
Определим постоянную времени первого каскада b1:
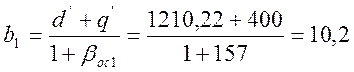
б) Аналогично для коэффициента передачи второго каскада записываем выражение:
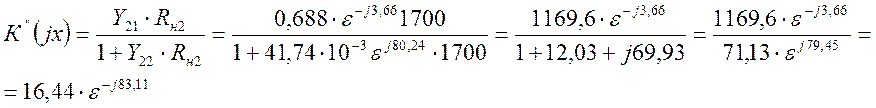
Определим коэффициент передачи второго каскада К2(jx) вторым способом:
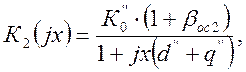 (2.22)
(2.22)
где ![]() -
коэффициент нагрузки;
-
коэффициент нагрузки;
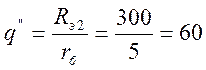 -
коэффициент местной обратной связи;
-
коэффициент местной обратной связи;
![]() -
коэффициент местной обратной связи;
-
коэффициент местной обратной связи;
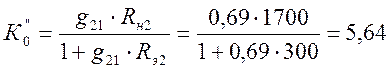 -
коэффициент усиления второго каскада на средних частотах.
-
коэффициент усиления второго каскада на средних частотах.
С учетом полученных значений и выражения (2.22) имеем:
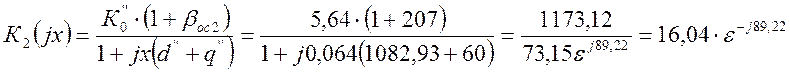
Определим постоянную времени второго каскада b2:
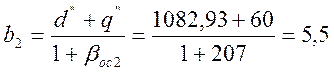
Проверяем выполнение условия:
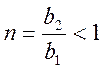 ,
(2.23)
,
(2.23)
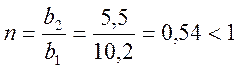 .
.
Условие (2.23) выполнено верно.
5)Тогда коэффициент усиления двухкаскадного усилителя без обратной связи:
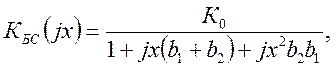 (2.24)
(2.24)
где ![]() -
коэффициент усиления двухкаскадного усилителя на средних частотах, который
может так же быть вычислен следующим образом:
-
коэффициент усиления двухкаскадного усилителя на средних частотах, который
может так же быть вычислен следующим образом:
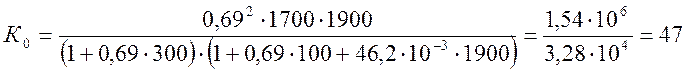
Подставляя известные величины в формулу (2.24) получаем коэффициент усиления усилителя без обратной связи:
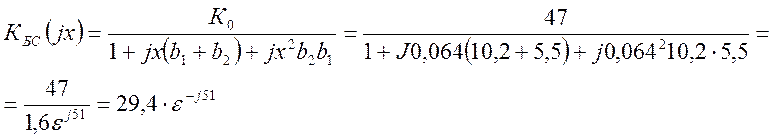
Для схемы “двойки” с ООС коэффициент усиления определяется формулой:
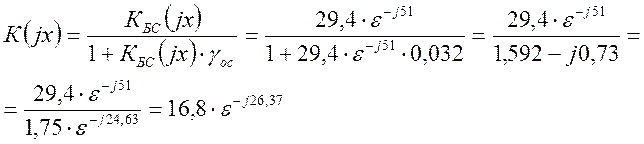
6) Определим коэффициент усиления двойки с учетом коэффициентов коррекции частотной характеристики:
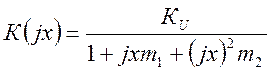 , (2.25)
, (2.25)
где ![]() - коэффициент усиления
двойки на средних частотах, определяемый как:
- коэффициент усиления
двойки на средних частотах, определяемый как:
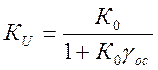 ,
(2.26)
,
(2.26)
Подставляя значения
известных величин К0 и ![]() в
выражение (2.26) определяем необходимую величину:
в
выражение (2.26) определяем необходимую величину:
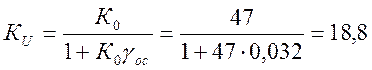
Определим коэффициенты коррекции частотной характеристики:
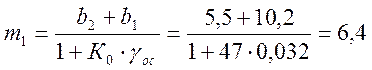
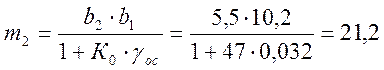
При чем должно выполняться условие:
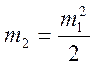 ,
(2.27)
,
(2.27)
Проверяем выполнение (2.27)
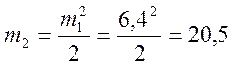 . Полученные значения m2 приблизительно равны
. Полученные значения m2 приблизительно равны ![]()
С учетом полученных величин и формулы (2.25) имеем, что:
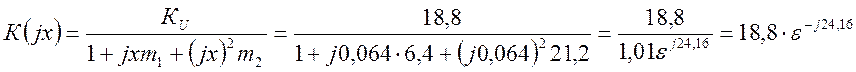
Из всех проведенных
расчетов видно, что рассчитанная величина К(jx) получилась больше чем заданная, то есть выполняется
условие ![]() :
:
![]() .
.
7) Для определения влияния коэффициентов m1 и m2 на частотную характеристику запишем нормированную комплексную передаточную характеристику “двойки”:
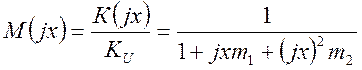 ,
(2.28)
,
(2.28)
Модуль М(jx) имеет вид:
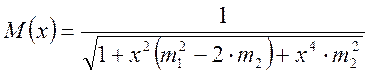 ,
(2.29)
,
(2.29)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.