Разработка оптического приемного устройства, страница 10

Таблица 3.2 - Значения для построения импульсной характеристики косинусоидального фильтра низких частот

, нсек
0	0	1
0,08	0,2	0,900
0,16	0,4	0,650
0,24	0,6	0,500
0,32	0,8	0,120
0,4	1,0	0
0,48	1,2	-0,026
0,56	1,4	-0,010
0,6	1,5	0
0,64	1,6	0,006
0,72	1,8	0,007
0,8	2,0	0

Рисунок 3.3 – Косинусоидальная характеристика передачи фильтра

1

0,5

Рисунок 3.4 – Импульсная характеристика фильтра с косинусоидальной функцией передачи

2

1

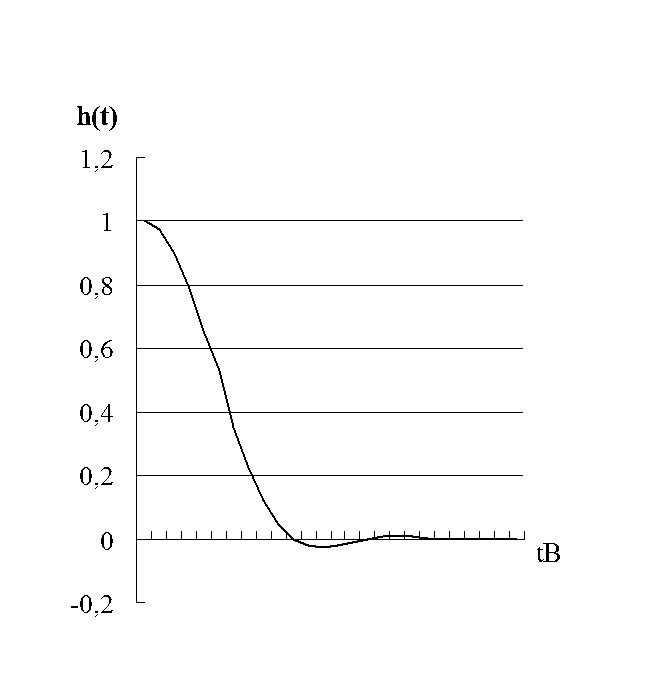
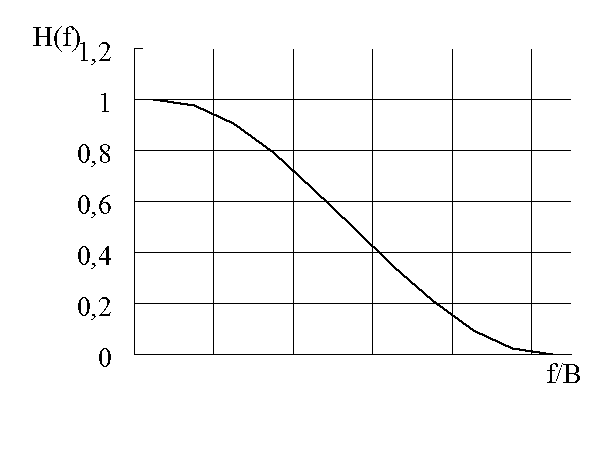
Несмотря на то, что идеальный фильтр низких частот нереализуем на практике, теоретически он обеспечивает наилучшее отношение сигнал/помеха. Однако, как видно из рисунка 3.2, этот фильтр создавал бы большие напряжения в соседних тактовых интервалах, а это означает, что совсем не большие эффекты уширения импульса или его дрожание вызывают  появление значительных взаимных искажений между символами. Фильтр с косинусоидальной функцией передачи вносит больше шумов, но имеет значительно больший допуск на дрожание и уширение импульса .

Реализуем фильтр с косинусоидальной функцией передачи . По заданной передаточной характеристике определим амплитудно-частотную характеристику (АЧХ) исходя из выражения:

.

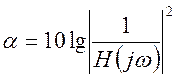Значения нормированной по частоте АЧХ приведены в таблице 3.3. Вид зависимости показан на рисунке 3.5.

Таблица  3.3 -  Нормированная по частоте АЧХ

параметр	Значение
Ω	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7
H(Ω)	1	0,976	0,905	0,794	0,655	0,5	0,346	0,21
α, дБ	0	0,21	0,87	2	3,67	6,02	9,22	13,56

Рисунок 3.5  - амплитудно-частотная характеристика

0,6

0,4

0,2

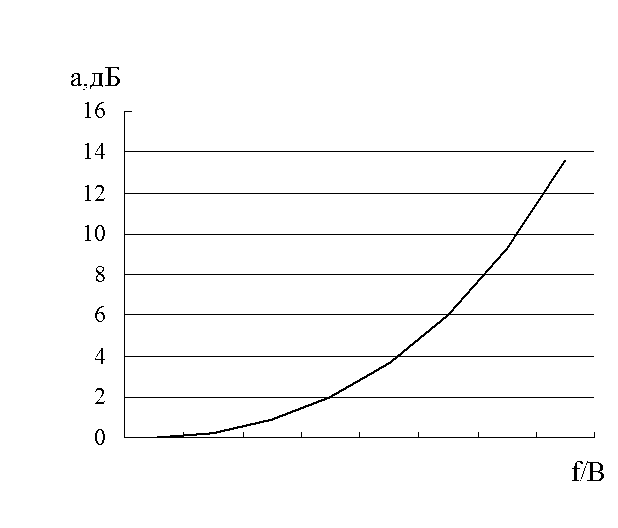
Аппроксимируем заданную АЧХ, применив метод интерполяции полиномом. Для этого на оси Ω=f/B  в рабочем диапазоне частот необходимо выбрать узлы интерполяции, которые размещаются с учетом особенностей характеристики α(Ω_i). Так как в данном случае характеристика не имеет ярко выраженных максимумов и минимумов, то количество узлов интерполяции примем равным двум и расположим их в точках Ω₁ = 0,2 и 0,7.

По значениям α(Ω_i) на узлах интерполяции находим рабочий коэффициент передачи из соотношения:

По найденным значениям находим функцию фильтрации , которая связана с рабочим коэффициентом передачи соотношением:

Результаты расчетов сведем в таблицу 3.4.

Таблица 3.4  - Требуемые значения функций на узлах интерполяции

Ωi	α(Ωi), дБ	S2(Ωi)
0,2	0,87	1,22	0,469
0,7	13,56	22,7	4,66

Порядок аппроксимирующего полинома и число коэффициентов С_i определяются число улов интерполяции q:

Полином будет полностью определен, если станут, известны коэффициенты С_i. Коэффициенты полинома определяются необходимой точностью соответствия заданной функции фильтрации и полученной в результате аппроксимации, то есть, справедлива система:

 

……….

Для нашего случая функция фильтрации имеет вид:

Составим систему уравнений для определения коэффициентов С_i:

Решая систему уравнений, получаем:

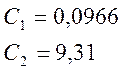
Таким образом, аппроксимирующая функция определена. Определим теперь аппроксимированный рабочий коэффициентом передачи из соотношения:

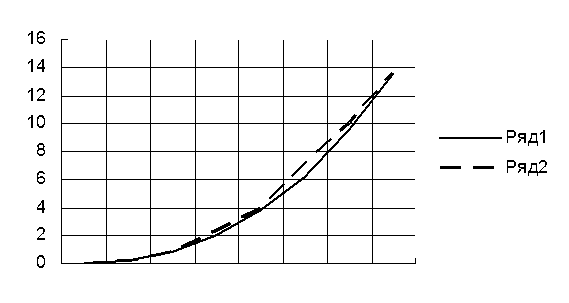
Оценим качество приближения заданной кривой α(Ω) (на рисунке 3.6 – ряд 1) и аппроксимированной α_а(Ω) (на рисунке 3.6 – ряд 2).  

	α(Ω), дБ

0,6

0,2

0,4

Ω

	Рисунок 3.6  - Амплитудно-частотная характеристика

Предположим, что приближение приемлемое, тогда заменяя в полученном выражении , получаем S(-р²):

Решаем уравнение S(-р²)=0 и определяем корни, расположенные в левой полуплоскости.

Пусть р²=х, тогда

,

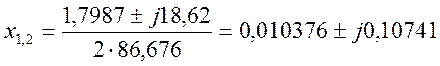 тогда

Корни, расположенные в левой полуплоскости – р₂ и р₄.

На основании корней, используя теорему Виета, получаем рабочий коэффициент передачи S(р):

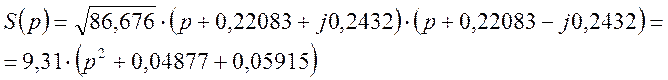
По функции S(р) находим передаточную функцию фильтра Т(р), подлежащую реализации:

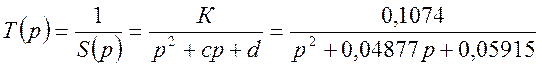
Найденная на этапе аппроксимации передаточная функция Т(р) может быть реализована как пассивными RLC – цепями, так и активными RC – цепями. Последние находят более широкое применение на практике в связи с возможностью их микроминиатюризации и малыми (по сравнению с пассивными схемами RLC) габаритами. В качестве активных элементов используются усилители с ограниченным коэффициентом усиления, операционные усилители, конверторы и т.д .