








ЛЕКЦИЯ 6
Тема 3.1. Упругие свойства кубических кристаллов. Упругие волны в кристаллах. Экспериментальное определение упругих констант.
Постоянные упругой жесткости кубических кристаллов.
Полное число упругих констант сокращается в зависимости от симметрии кристалла. Так, если кристалл обладает триклинной симметрией, то полное число упругих констант равно 21.
Число независимых постоянных упругой жесткости может
быть уменьшено и дальше. Так для кубических кристаллов остаются лишь три независимые
постоянные. Основное свойство кубических кристаллов состоит в том, что
направления ![]() взаимно перпендикулярны и
полностью эквивалентны. Это приводит к тому, что имеют место такие соотношения:
взаимно перпендикулярны и
полностью эквивалентны. Это приводит к тому, что имеют место такие соотношения:
![]() .
.
Остальные компоненты Сij равны нулю. Так что для кубического кристалла имеется всего лишь три независимых компоненты С11, С44 и С12 и набор постоянных упругой жесткости сводится к матрице
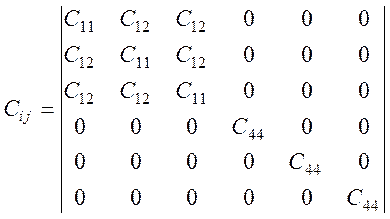 (3.26)
(3.26)
Закон Гука для кубических кристаллов с учетом (3.26) имеет вид
![]()
![]()
![]()
![]()
![]()
![]() (3.27)
(3.27)
Для кубических кристаллов постоянные упругой жесткости и податливости связаны между собой следующими соотношениями:
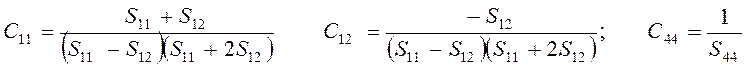 (3.28)
(3.28)
Эти соотношения получаются из вычисления матрицы, обратной (3.26).
Упругие волны в кристаллах
Процессы распространения упругих волн в кристаллах много сложнее процессов распространения электромагнитных волн. Электромагнитные волны всегда поперечны, упругие (звуковые) волны в кристаллах могут быть поперечными и продольными. Продольные волны – волны сжатий и растяжений, поперечные – волны деформаций сдвига. В каждом заданном направлении в кристалле распространяются в общем случае три поляризованные упругие волны с разными скоростями.
Рассмотрим распространение упругих волн в кубическом
кристалле, плотность которого равна ρ. Внутри кристалла выберем
элементарный куб с ребрами ![]() , параллельным
кристаллографическим осям координат x, y, z. При движении упругой волны по кристаллу каждая грань
элементарного куба под действием напряжения
, параллельным
кристаллографическим осям координат x, y, z. При движении упругой волны по кристаллу каждая грань
элементарного куба под действием напряжения ![]() совершает
небольшие перемещения (в области упругости, когда справедлив закон Гука).
Найдем уравнение движения для поступательного перемещения элементарного куба
при распространении упругой волны вдоль оси x.
совершает
небольшие перемещения (в области упругости, когда справедлив закон Гука).
Найдем уравнение движения для поступательного перемещения элементарного куба
при распространении упругой волны вдоль оси x.
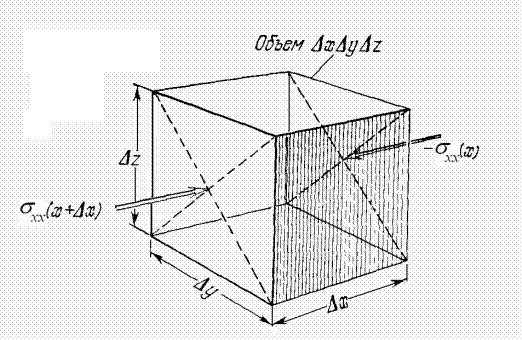
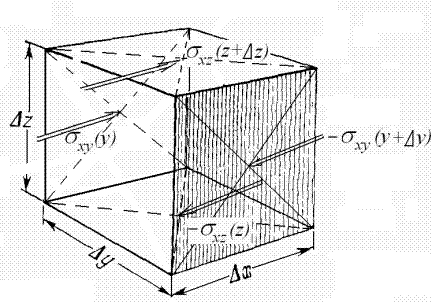 На элемент объема
На элемент объема ![]() действует
напряжение –
действует
напряжение –![]() на грань х и
на грань х и 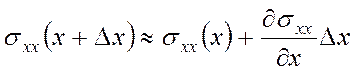 на параллельную грань
на параллельную грань ![]() (см рис. 3.7а). Результирующая
сила равна
(см рис. 3.7а). Результирующая
сила равна 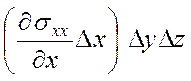 . Другие силы, действующие в
направлении оси х, вызваны изменением внутри куба напряжений
. Другие силы, действующие в
направлении оси х, вызваны изменением внутри куба напряжений ![]() и
и ![]() , и
показаны на рис. 3.7б.
, и
показаны на рис. 3.7б.
 а)
б)
а)
б)
Рисунок 3.7 – Силы, действующие на элемент объема в кристалле
при движении упругой волны вдоль оси х
Результирующая х- компонента силы, действующей на куб, равна
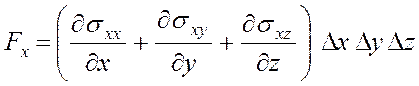 (3.29)
(3.29)
Сила равна массе куба, умноженной на х- компоненту
ускорения. Масса равна ![]()
![]() ,
а ускорение
,
а ускорение 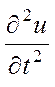 , где u
– компонента вектора смещения центра масс куба вдоль оси x.
Согласно второму закону Ньютона, уравнение движения для смещения u
под действием напряжений принимает вид:
, где u
– компонента вектора смещения центра масс куба вдоль оси x.
Согласно второму закону Ньютона, уравнение движения для смещения u
под действием напряжений принимает вид:
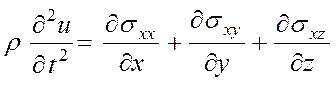 (3.30)
(3.30)
Аналогичные уравнения будут иметь место для осей у и z. Из соотношения (3.27) следует, что для кубического кристалла справедливо выражение
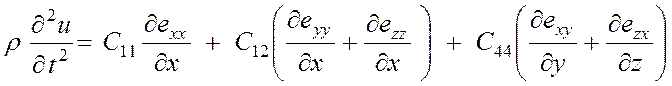 (3.31)
(3.31)
направления координатных осей х, у, z параллельны ребрам куба.
Используя выражения (3.7) и (3.11) для компонент деформации, имеем:
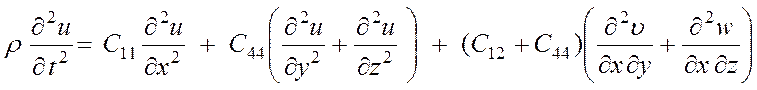 , (3.32а)
, (3.32а)
где u, υ, w — компоненты вектора смещения R [см. выражение (3.5)].
Соответствующие уравнения движения для смещений υ и w получаются непосредственно из (3.32а) круговой перестановкой:
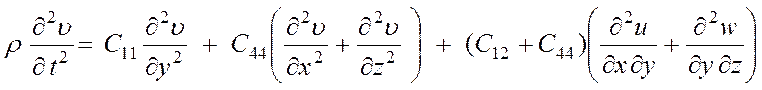 ,
,
(3.32б)
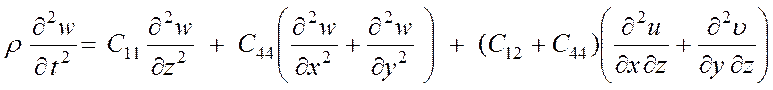 .
.
(3.32в)
Соотношения (3.32а) - (3.32в) представляют собой систему трех дифференциальных волновых уравнений, решения которых будем искать, выбрав динамически меняющиеся во времени и пространстве смещения в виде плоских волн.
Найдем простые решения этих уравнений для некоторых частных случаев.
Волны в направлении [100]. Одним из решений уравнения (3.32а) будет служить продольная волна
![]() (3.33)
(3.33)
где
u — это х-компонента смещения частицы. Волновой
вектор и смещение частицы направлены вдоль ребра куба, совпадающего по
направлению с осью х. Здесь – волновой
вектор и
– волновой
вектор и ![]() – угловая частота. Подставляя (3.33)
в (3.32а), получим:
– угловая частота. Подставляя (3.33)
в (3.32а), получим:
![]() , (3.34)
, (3.34)
следовательно, фазовая скорость распространения продольной волны в направлении [100] равна
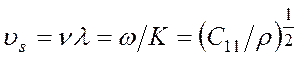 (3.35)
(3.35)
Другим решением системы уравнений (3.32а) - (3.32в) будет служить поперечная волна или волна сдвига с волновым вектором, направленным вдоль ребра куба, совпадающего по направлению с осью х; смещение частицы υ происходит в направлении оси у:
![]() (3.36)
(3.36)
Это второе решение дает после подстановки в (3.32б) дисперсионное соотношение
![]() (3.37)
(3.37)
из которого следует, что скорость поперечной волны ω/К в направлении [100] равна
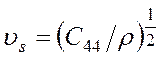 (3.38)
(3.38)
Аналогичное выражение для скорости получается при движении частиц вдоль оси z.
Таким образом, для волнового вектора К, параллельного направлению [100], распространяются три независимых упругих волны: одна продольная и две поперечные волны сдвига (см. рис. 3.8 а). Сдвиговые волны в данном направлении неразличимы по скоростям, их поляризация лежит в плоскости (100), перпендикулярной направлению распространения. Скорость продольной волны определяется только константой С11, а скорость сдвиговой — только константой С44. Измерив скорости этих волн, можно определить соответствующие упругие константы.
Направления, в которых скорости сдвиговых волн одинаковы, называются акустическими осями.
Таблица 3.1. Упругие волны в направлении [100] в кубических кристаллах
|
Направление смещения (поляризация) |
Тип волны |
Скорость |
|
Лежит в плоскости (100) [100] |
Т L |
|
Волны в направлении [110]. Особый интерес представляет случай распространения упругих волн в направлении диагонали грани куба в кубическом кристалле, так как в этом случае довольно просто определить все три упругие постоянные, если известны скорости распространения трех типов волн в этом направлении.
Рассмотрим сначала волну сдвига, распространяющуюся в плоскости ху; смещение w частицы направлено вдоль оси z:
![]() (3.39)
(3.39)
тогда, используя (3.32в), получаем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.