Упругие свойства кубических кристаллов. Упругие волны в кристаллах. Экспериментальное определение упругих констант, страница 2

                           (3.40)

Полученный результат не зависит от направления распространения волны в плоскости ху. Рассмотрим другие волны, распространяющиеся в плоскости ху; смещение частицы происходит в этой же плоскости:

,             (3.41)

Из(3.32а) и (3.32б) получаем:

                  (3.42)

Эти два уравнения имеют особенно простое решение для волны, распространяющейся в направлении [110]; для этого направления . Условием существования нетривиальных решений является равенство нулю определителя, составленного из коэффициентов при u и υ в уравнениях (3.41):

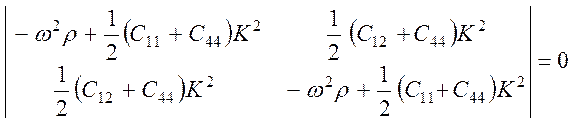                  (3.43)

Это квадратное относительно   уравнение имеет корни

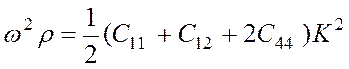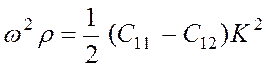,                       (3.44)

Как увидим далее, первый корень описывает продольную волну, второй — поперечную. Для получения направления смещения частицы подставляем первый корень в уравнение (3.42); получаем:

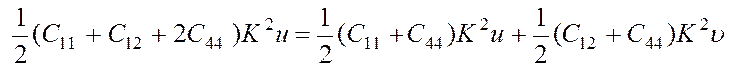      (3.45)

откуда получаем, что  . Таким образом, смещение частицы происходит вдоль направления [110] параллельно вектору К (рис. 3.8). Подставляя второй корень в уравнение (3.42), получаем:

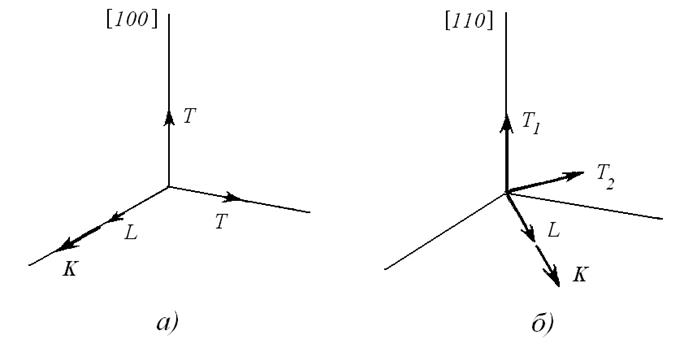
Рисунок 3.8 -  Эффективные упругие постоянные, определяемые из измерения

 скоростей трех типов упругих волн, распространяющихся

в главных направлениях в кубических кристаллах:

а) волна в направлении [100], измеряются С₁₁  для L и C₄₄ для Т;

б) волна в направлении [110], измеряются 1/2(С₁₁ + С₁₂ + 2С₄₄) для L,

С₄₄  для T₁ и 1/2(С₁₁ — С₁₂) для Т_2.

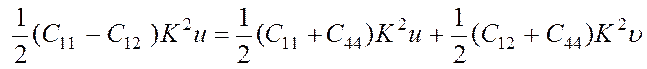,           (3.46)

откуда . Направление смещения частицы совпадает с направлением [] и перпендикулярно к вектору К.

Общий результат для направления распространения [110] состоит в том, что распространяются три независимых упругих волны, из которых одна — продольная L(longitudinal) и две — сдвиговые Т₁ и Т₂, скорости всех трех волн различны (их можно определить из выражений (3.40) и (3.44)) и заданы определенными комбинациями упругих постоянных (табл. 3.2). Из анализа табл. 3.2 следует, что, измерив скорости упругих волн в данном направлении, можно получить 3 независимых уравнения для определения всех трех упругих констант кубического кристалла. Ясно также, что смещения всех трех волн составляют тройку ортогональных векторов.

      Таблица 3.2. Упругие волны в направлении [110] кубических кристаллов

Направление смещения (поляризация)	Тип волны	Скорость
[001] [] [110]	Т1 Т2 L

Качественно аналогичные результаты могут быть получены и для других направлений в кубическом кристалле:

1) для волнового вектора К, имеющего данную величину и данное направление, распространяются три независимых упругих волны, каждая со своей скоростью. В частных случаях акустических осей скорости сдвиговых волн совпадают;

2) упругие смещения, соответствующие этим волнам, образуют ортогональную тройку векторов.

Анализировать характер распространения упругих волн в кристаллах в этих частных направлениях намного проще, чем в произвольных направлениях.

Уравнения, подобные приведенным в табл. 3.1 и 3.2 могут быть получены и для кристаллов произвольной симметрии. Отметим, что направление колебаний (их поляризация) в общем случае не строго параллельно или перпендикулярно К. Измеряя скорости звуковых волн различных типов в определенных направлениях, можно вычислить, с учетом возможных других эффектов, все компоненты тензора упругих постоянных.

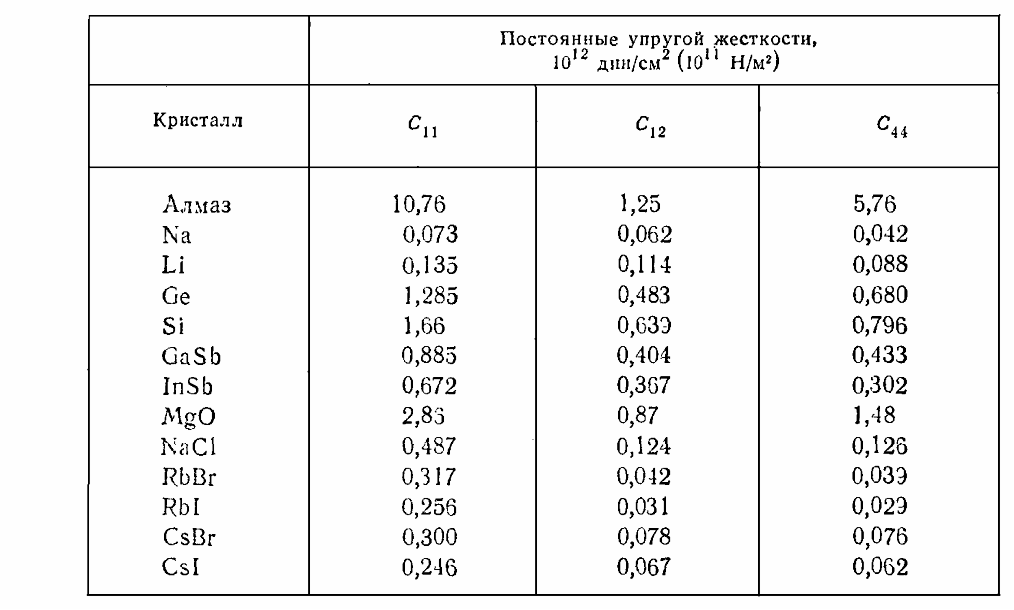
Значения адиабатических постоянных упругой жесткости С₁₁, С₁₂ и С₄₄ ряда кубических кристаллов при комнатной температуре приведены в табл. 3.3.

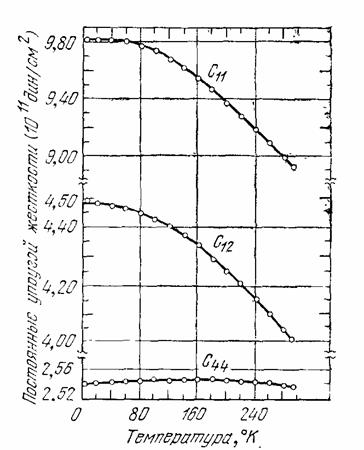
Отметим общую тенденцию для постоянных упругой жесткости: они уменьшаются с увеличением температуры. Температурная зависимость постоянных упругой жесткости BaF₂  показана на рис. 3.9.

Таблица 3.3. Значения адиабатических постоянных упругой жесткости ряда

кубических кристаллов при комнатной температуре 300 К

Экспериментальное определение упругих констант.

Существует довольно большое количество динамических методов определения упругих констант. Одним из наиболее удобных является метод ультразвуковых импульсов,  получивший широкое распространение. Принцип этого метода основан на измерении времени распространения ультразвукового импульса в исследуемом образце.  В ультразвуковом методе кварцевый пьезоэлектрический преобразователь с металлическим электродами для подачи высокочастотного электрического поля приклеен к поверхности кристалла. Пластинка из кристалла кварца может быть вырезана таким образом, что через нее будет распространяться либо продольная, либо поперечная волна при возбуждении высокочастотным электрическим полем. Ультразвуковой импульс от кварцевого преобразователя проходит через исследуемый кристалл и, отразившись от его задней грани, возвращается обратно к преобразователю (рис. 3.10). Интервал времени между испусканием импульса и его приемом измеряется с помощью стандартной электронной схемы. Скорость распространения получается от деления общего пути на время прохождения. В описываемом устройстве частота может составлять 15 МГц, а продолжительность импульса 1 мксек. Длина волны порядка 3^.10^{-4 м. Линейные размеры образца могут быть порядка 1 см.}

Три постоянные упругой жесткости С₁₁, С₁₂ и С₄₄  можно определить, зная скорость распространения трех типов волн, которые были отмечены выше. Для всех трех типов волн может быть использован кристаллический образец одной и той же ориентировки, но необходимо изменять срез и установку кварцевого кристаллического преобразователя, для того чтобы создать требуемое направление движения частиц в кристаллическом образце.

Ультразвуковой метод используют и для определения упругих постоянных третьего порядка. Как известно, в области применимости закона Гука плотность упругой энергии квадратична относительно компонент деформации. Вне этой области появляются произведения деформаций более высокого порядка. Постоянные упругой жесткости третьего порядка связывают упругую энергию с произведениями трех компонент деформации. Эти постоянные являются постоянными самого низшего порядка из всех постоянных, входящих в описание нелинейных эффектов, таких, например, как взаимодействие фононов и термическое расширение. Постоянные третьего порядка могут быть определены из измерения скоростей звуковых волн с малыми амплитудами в статически напряженной среде.

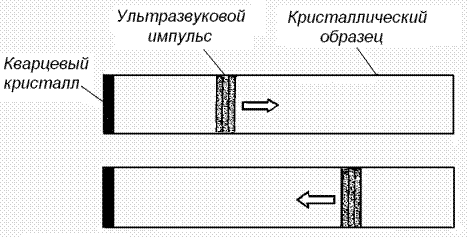
Рисунок 3.10 -. Метод ультразвуковых импульсов, используемом для определения скоростей упругих волн. Ультразвуковой импульс генерируется пьезоэлектрическим преобразователем, проходит через исследуемый кристалл и, отразившись от его задней грани, возвращается обратно к преобразователю. Фиксируется интервал времени между моментом испускания импульса и его приемом.