Министерство образования и науки Российской Федерации
ГОУ ВПО Сибирский государственный индустриальный университет
Кафедра инженерных конструкций
Отчет
по практическим занятиям по курсу:
"Основы метрологии и стандартизации в строительстве"
Дзарасов М.В.
Руководитель: Матвеев А.А.
г. Новокузнецк,2004г.
|
Множитель |
Наименование |
Обозначение |
Множитель |
Наименование |
Обозначение |
||
|
Русское |
Международное |
Русское |
Международное |
||||
|
109 |
гига |
Г |
G |
10-9 |
нано |
н |
n |
|
106 |
мега |
М |
M |
10-6 |
микро |
мк |
m |
|
103 |
кило |
к |
k |
10-3 |
милли |
м |
m |
|
102 |
гекто |
г |
h |
10-2 |
санти |
с |
c |
|
101 |
дека |
да |
da |
10-1 |
деци |
д |
d |
|
Единицы механического напряжения |
МПа=Н/мм2 |
кгс/мм2 |
кгс/см2 |
|
МПа=Н/мм2 |
1 |
0,102 |
10,197 |
|
кгс/мм2 |
9,807 |
1 |
100 |
|
кгс/см2 |
0,098 |
0,01 |
1 |
1 МПа = 1 Н/мм2 = 1/9,807 кгс/мм2 = 0,102 кгс/мм2 = 1/9,807×102 кгс/см2 = 10,197 кгс/см2
1 кгс/мм2 = 9,807 Н/мм2 = 1×102 кгс/см2 = 100 кгс/см2
1 кгс/см2 = 9,807 Н/см2 = 9,807×10-2 Н/мм2 = 0,098 Н/мм2 = 10-2 кгс/мм2
Таблица 3 – Связь между единицами коэффициента интенсивности напряжения
|
Единицы коэффициента интенсивности напряжения |
Н/мм3/2 |
МПа× |
кгс/мм3/2 |
|
Н/мм3/2 |
1 |
10-6 |
0,102 |
|
МПа× |
106 |
1 |
0,102×106 |
|
кгс/мм3/2 |
9,807 |
9,807×10-6 |
1 |
1 Н/мм3/2 = 10-6 МН/мм3/2 = 1/9,807 кгс/мм3/2 = 0,102 кгс/мм3/2
1 МПа×![]() = 1 МН/мм3/2 = 106 Н/мм3/2
= 1/9,807×106 кгс/мм3/2 = 0,102×106 кгс/мм3/2
= 1 МН/мм3/2 = 106 Н/мм3/2
= 1/9,807×106 кгс/мм3/2 = 0,102×106 кгс/мм3/2
1 кгс/мм3/2 = 9,807 Н/мм3/2 = 9,807×10-6 МН/мм3/2
Таблица 4 – Связь между единицами энергии (работы)
|
Единицы энергии (работы) |
Дж |
кгс×м |
кал |
|
Дж |
1 |
0,102 |
0,239 |
|
кгс×м |
9,807 |
1 |
2,342 |
|
кал |
4,1868 |
0,427 |
1 |
1 Дж = 1 Н×м = 1/9,807 кгс×м = 0,102 кгс×м = 1/4,1868 кал = 0,2388 кал
1 кгс×м = 9,807 Н×м = 9,807 Дж =9,807/4,1868 кал = 2,342 кал
1 кал = 4,1868 Дж = 4,1868/9,807 кгс×м = 0,4269 кгс×м
Определение измеряемой величины по классу точности прибора
1) Класс точности 1,6
Шкала от 0 до 100 В
Показание 20 В
Uизм – ?
![]() .
.
2) Класс точности 0,5
Шкала от (-50) до (+50) А
Показание -25 А
Iизм – ?
![]() .
.
3)
Класс точности 1,7![]()
Шкала от 0 до 500 Ом
Rизм – ?
![]() .
.
4)
Класс точности 2,5![]()
Шкала от 0 до ∞ Ом
Показание 200 МОм
Rизм – ?
![]() .
.
5) Класс точности 0,05/0,02
Шкала ±150
Показание (-75) А
Iизм – ?
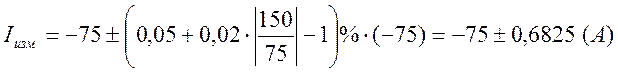 .
.
Первичная обработка, корреляционный и регрессионный анализ данных.
|
N |
X |
Y |
ΔX=Xi-Xср |
ΔY=Yi-Yср |
(ΔX)2 |
(ΔY)2 |
ΔXi*ΔYi |
|
|
1 |
177,00 |
175,00 |
-9,70 |
-6,60 |
94,09 |
43,56 |
64,02 |
|
|
2 |
182,00 |
191,00 |
-4,70 |
9,40 |
22,09 |
88,36 |
-44,18 |
|
|
3 |
181,00 |
183,00 |
-5,70 |
1,40 |
32,49 |
1,96 |
-7,98 |
|
|
4 |
179,00 |
175,00 |
-7,70 |
-6,60 |
59,29 |
43,56 |
50,82 |
|
|
5 |
187,00 |
183,00 |
0,30 |
1,40 |
0,09 |
1,96 |
0,42 |
|
|
6 |
179,00 |
179,00 |
-7,70 |
-2,60 |
59,29 |
6,76 |
20,02 |
|
|
7 |
182,00 |
180,00 |
-4,70 |
-1,60 |
22,09 |
2,56 |
7,52 |
|
|
8 |
177,00 |
175,00 |
-9,70 |
-6,60 |
94,09 |
43,56 |
64,02 |
|
|
9 |
181,00 |
175,00 |
-5,70 |
-6,60 |
32,49 |
43,56 |
37,62 |
|
|
10 |
186,00 |
178,00 |
-0,70 |
-3,60 |
0,49 |
12,96 |
2,52 |
|
|
11 |
193,00 |
191,00 |
6,30 |
9,40 |
39,69 |
88,36 |
59,22 |
|
|
12 |
184,00 |
176,00 |
-2,70 |
-5,60 |
7,29 |
31,36 |
15,12 |
|
|
13 |
202,00 |
191,00 |
15,30 |
9,40 |
234,09 |
88,36 |
143,82 |
|
|
14 |
182,00 |
185,00 |
-4,70 |
3,40 |
22,09 |
11,56 |
-15,98 |
|
|
15 |
191,00 |
179,00 |
4,30 |
-2,60 |
18,49 |
6,76 |
-11,18 |
|
|
16 |
198,00 |
178,00 |
11,30 |
-3,60 |
127,69 |
12,96 |
-40,68 |
|
|
17 |
200,00 |
192,00 |
13,30 |
10,40 |
176,89 |
108,16 |
138,32 |
|
|
18 |
184,00 |
173,00 |
-2,70 |
-8,60 |
7,29 |
73,96 |
23,22 |
|
|
19 |
203,00 |
175,00 |
16,30 |
-6,60 |
265,69 |
43,56 |
-107,58 |
|
|
20 |
186,00 |
198,00 |
-0,70 |
16,40 |
0,49 |
268,96 |
-11,48 |
|
|
X ср= |
186,700 |
axy= |
0,2944841 |
Σ(ΔXi*ΔYi)= |
387,60 |
|||
|
Y ср= |
181,600 |
ayx= |
0,3789597 |
|||||
|
Σ(ΔXI)2 |
1316,200 |
Syx= |
6,9154973 |
|||||
|
Σ(ΔYI)2 |
1022,800 |
Sxy= |
7,8449287 |
|||||
|
Sx= |
8,323 |
Δyx=+/- |
14,4533894 |
|||||
|
Sy= |
7,337 |
Δxy=+/- |
16,3959009 |
|||||
|
ΔX=+/- |
3,890 |
|||||||
|
ΔY=+/- |
3,429 |
|||||||
|
γx= |
2,138 |
|||||||
|
γy= |
1,937 |
|||||||
|
rxy= |
0,334 |
|||||||
1. Первичная обработка данных
- определение средних величин
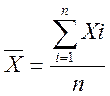 ;
; 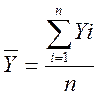 ;
;
![]() =186,700 ;
=186,700 ; ![]() =181,600;
=181,600;
- определение частных отклонений
![]() ;
;
![]() ; смотри таблицу
; смотри таблицу
-определение квадратов частных отклонений
![]() ;
;
![]() ; смотри таблицу
; смотри таблицу
-определение суммы квадратов частных отклонений
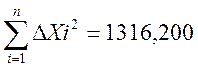 ;
; 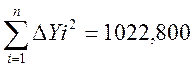 ;
;
- определение среднеквадратического отклонения
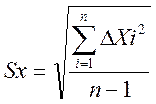 =8.323;
=8.323; 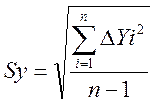 = 7.337
= 7.337
задаемся уровнем доверительной вероятности 5% и определяем квантиль Стьюдента
![]()
-определение отклонений
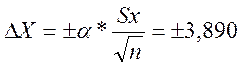 ;
; 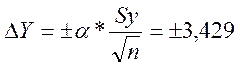 ;
;
-определение относительной погрешности обработки
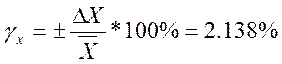 ;
; 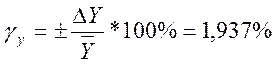 ;
;
2. Регрессионный и корреляционный анализ данных
- определяем коэффициент корреляции
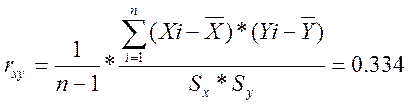 ;
;
- определяем коэффициенты уравнений
![]() ;
; ![]() ;
;
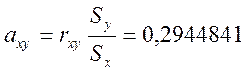 ;
; 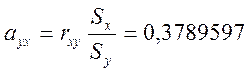 ;
;
- определим среднеквадратичное отклонение для линии регрессии
![]() ;
; ![]() ;
;
- определим ширину доверительного интервала для линии регрессии
![]() ;
; ![]() ;
;
- строим график для прямых:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.