Изучение плоского ламинарного течения несжимаемой жидкости в тройнике при помощи CFD программы σFlow

ЛАБОРАТОРНАЯ РАБОТА №3

ЛАМИНАРНОЕ ТЕЧЕНИЕ ЖИДКОСТИ В ТРОЙНИКЕ

Цель работы: Изучение плоского ламинарного течения несжимаемой жидкости в тройнике при помощи CFD программы σFlow.

Оборудование: ПЭВМ, компьютерная программа σFlow, Microsoft Office.

Краткие теоретические сведения и постановка задачи

Тройник это элемент трубопровода, применяющийся для слияния или разделения потоков. В природе и технике существует множество разнообразных по форме и размерам тройников. Основной характеристикой тройника является гидродинамическое сопротивление, для вычисления которого в большинстве случаев ограничиваются данными из справочников. К сожалению, эмпирические данные не могут обобщить всё многообразие форм тройников и режимов течения, которые в них реализуются. Альтернативным эксперименту способом вычисления гидродинамического сопротивления, какой либо конструкции может служить численное моделирование. Для демонстрации этого проведем расчет двумерного ламинарного течения в тройнике.

Тройник представляет собой канал прямоугольного сечения, к которому под прямым углом подсоединен другой прямоугольный канал  как показано на рис 1. Характерные размеры тройника L = 3 м и W = 1 м. Высота канала в направлении оси Z равна 2.11 м.

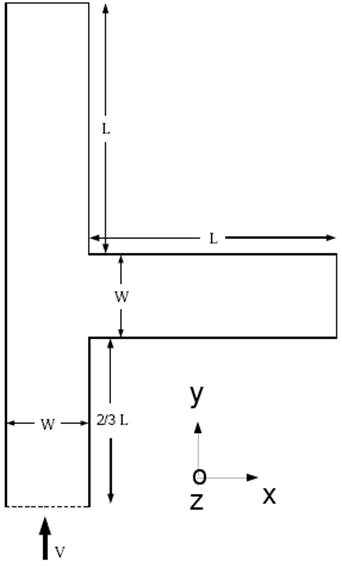
Рис.1. Геометрия задачи

Расчеты будем проводить для чисел Рейнольдса равных .  Число Рейнольдса для данной задачи определяется по формуле:

,

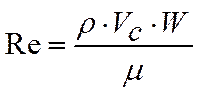где  – плотность потока,  – динамическая вязкость,  – скорость жидкости в центре канала на входе в тройник, – ширина входа. Плотность будем задавать равной единице.  Для соответствующих чисел Рейнольдса динамическая вязкость приведена в таблице 1. На входе в тройник будем задавать величину массового расхода 0,667 кг/с.  На выходах из тройника будем задавать давление равным нулю. Для проведения двухмерных расчетов на стенках тройника, параллельных плоскости Z, поставим условия скольжения. На остальных стенках условие прилипания.

Таб. 1. Динамическая  вязкость.

Число Рейнольдса,   Re	10	100	200	300	400
Вязкость,     ,      Па·с	0.1	0.01	0.005	0.00333	0.0025

Порядок выполнения работы

Создание геометрии объекта и построение расчетной сетки

Запускаем программу GridEdit.exe.

а)

б)

в)

Рис.2. а) Задание узлов. б) Соединение узлов линиями. в) Выделение объектов рамкой

Открываем окно «Точки» (рис.2.а) и задаем в нем координаты четырех точек соответствующих входу в тройник, верхнему и боковому выходу из тройника. Координаты этих точек будут -2.5 0.0 0.0; -0.5 0.0 0.0; 0.5 0.0 0.0; 3.5 0.0 0.0. Нажимаем “Добавить”. Теперь необходимо соединить построенные точки. Для этого выбираем окно “Линии” (рис.2.б). В нем выбираем “Отрезок”, ставим галочку “Через точки” и при открытом окне “Линии” выполняем соединение точек отрезками. Чтобы это сделать нужно “кликнуть” мышкой сначала на одну точку затем на вторую, если все верно, то точки соединятся прямой линией. После последовательного соединения всех точек мы получили линию, состоящую из трех отрезков (рис.2б). Теперь нам необходимо скопировать эту линию вдоль оси Y на расстояние 1м с оставлением следа (т.е. точки исходной и скопированной линий будут соединены отрезками). Для этого необходимо закрыть окно “Линии” и открыть меню “Трансформация”. Далее инструментом “Рамка” и мышью выделяем построенную нами линию (рис.2в). Выделенные объекты прорисовываются белым цветом. В закладке “Перемещение” ставим галочки “НА”, “+Выполнить”, “+След”. В столбце “Y” напротив галочки “НА” ставим величину перемещения 1м (рис.3а). Нажимаем на кнопку “Копировать”. Скопированная линия выделена белым цветом, поэтому ее можно скопировать на расстояние 3м. Для этого нужно в столбце “Y” 1 заменить на 3 и нажать “Копировать” (рис.3б).

 

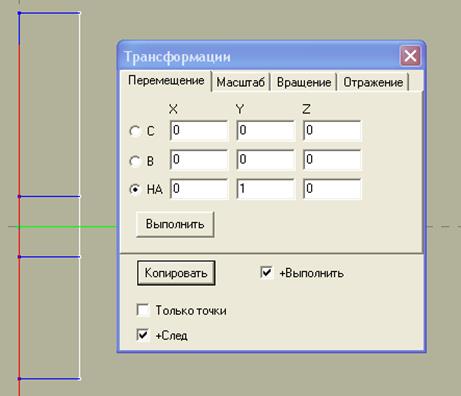
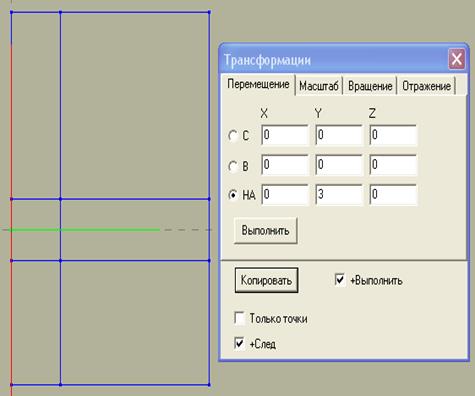
                                 а)                                          б)

Рис.3. Копирование линии с оставлением следа

Далее выделяем получившийся прямоугольник и аналогичным образом копируем его вдоль оси Z на расстояние 2.11м (рис.4). Выбор такого расстояния обусловлен тем, что площадь входа в этой версии программы не совпадает с площадью окна (см. документацию), поэтому для того чтобы площадь входа равнялась 1м² высоту канала необходимо сделать равной 2.11м.

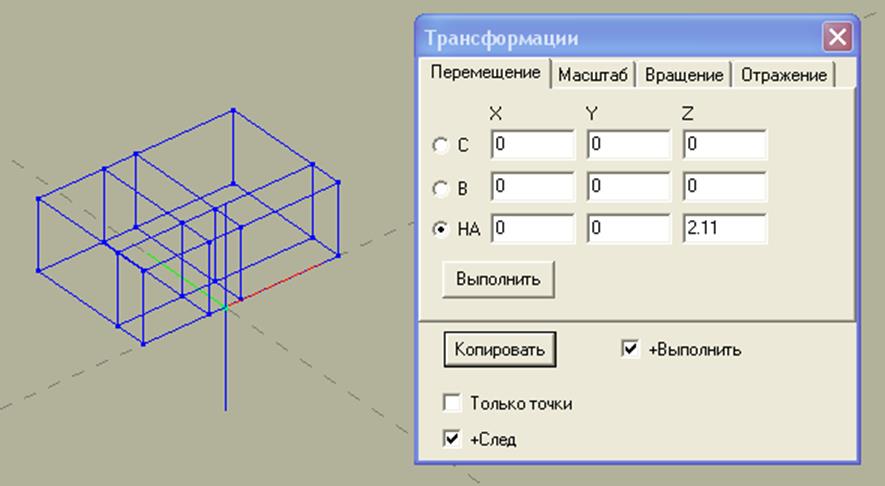
Рис.4. Копирование прямоугольника

Геометрия объекта построена, теперь проверим ее на наличие ошибок. Чтобы это сделать необходимо в инструменте “Соединения” нажать кнопки “Авто” а затем “Анализ геометрии” (рис. 5).

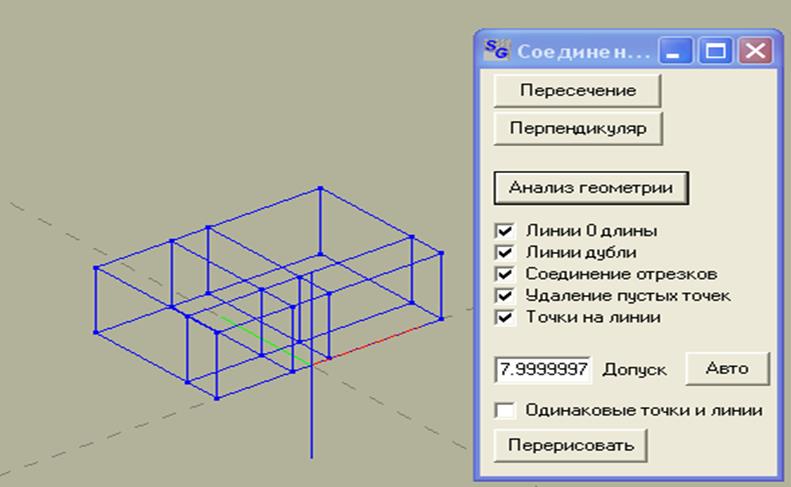
Рис.5. Проверка геометрии на наличие ошибок

Разбиваем построенную геометрию на блоки. Для этого нажимаем “Поиск блоков”. Если геометрия построена правильно найденные блоки будут нарисованы зеленым цветом (рис.6). В данном случае их будет шесть.

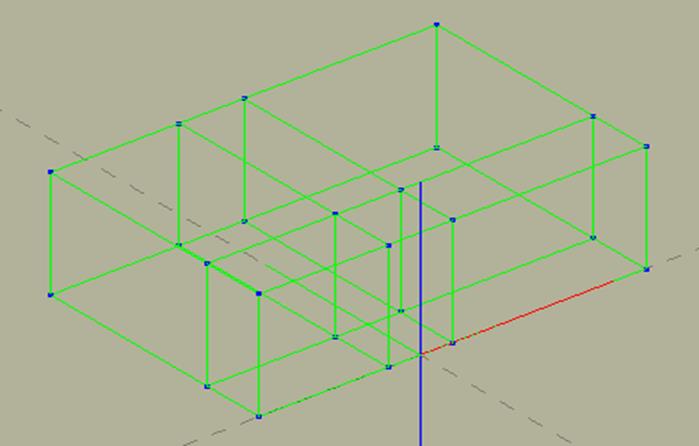
Рис.6. Разбивка геометрии на блоки

Для построения расчетной сетки необходимо на панели инструментов выбрать элемент “Сетка” (рис. 7). Далее выделяем мышкой в построенной геометрии начальную точку (точку с которой пойдет нумерация узлов сетки) нажимаем кнопку “Начальная точка”. Кнопками

“Напр.IJK” и “I<->J” устанавливаем необходимое направление сеточных координат I, J, K.

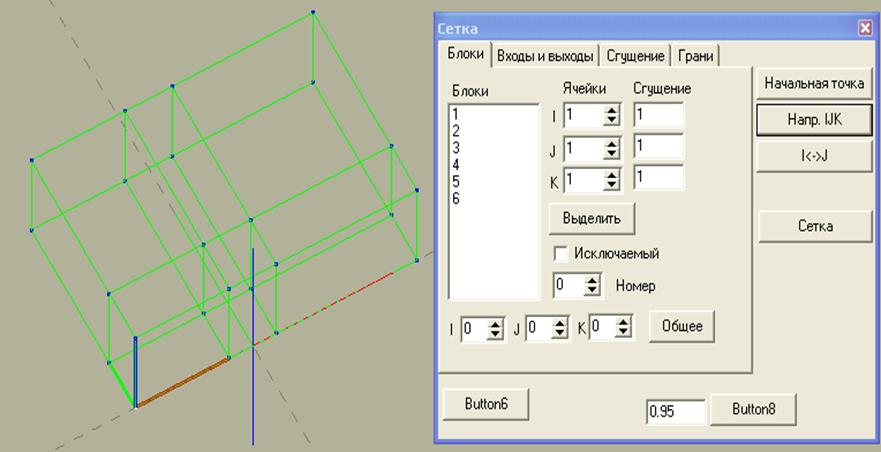
Рис.7. Задание начальной точки

В окнах ввода (напротив кнопки “Общее”) задаем количество узлов сетки по каждому направлению. Для данной задачи возьмем например 91×91×3 узла (рис.8.). Нажимаем кнопку “Общее”, а затем кнопку “Сетка”. Для того чтобы увидеть построенную сетку, в меню “Вид” необходимо поставить галочку напротив “Сетка.”

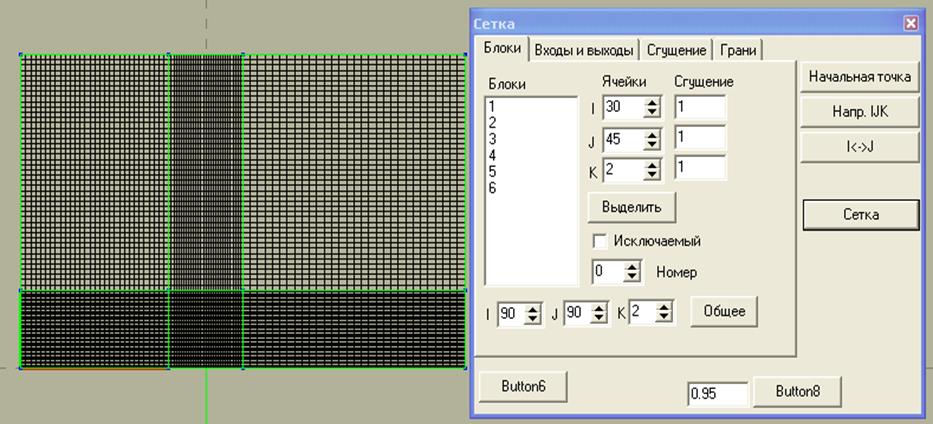
Рис.8. Построение первоначального варианта сетки

Видно, что эта сетка достаточно не равномерна. Для того чтобы ее подкорректировать в окне “Блоки” Мышкой выбираем нужный блок и в окнах ввода “Ячейки” задаем нужное количество узлов уже именно в этом блоке (рис.9).

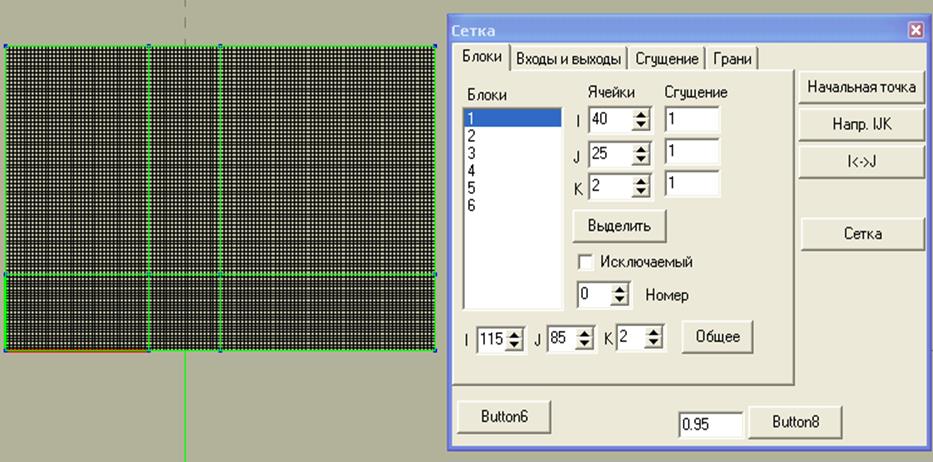
Рис.9. Скорректированная сетка

После того как мы скорректировали нашу сетку, она стала состоять из 116×86×3 узлов. Теперь сделаем блокировку блоков 4 и 6. Для этого выделяем их номера мышкой в окне “Блоки” и ставим галочку “Исключаемый”, после этого жмем “Сетка”. Проделав это, получаем сетку представленную на рисунке 10.

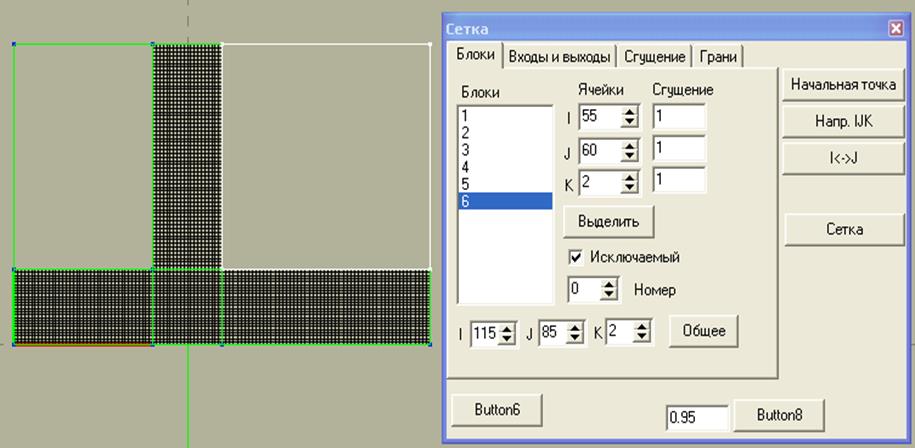
Рис. 10. Блокировка областей