Изучение плоского ламинарного течения несжимаемой жидкости в тройнике при помощи CFD программы σFlow, страница 3

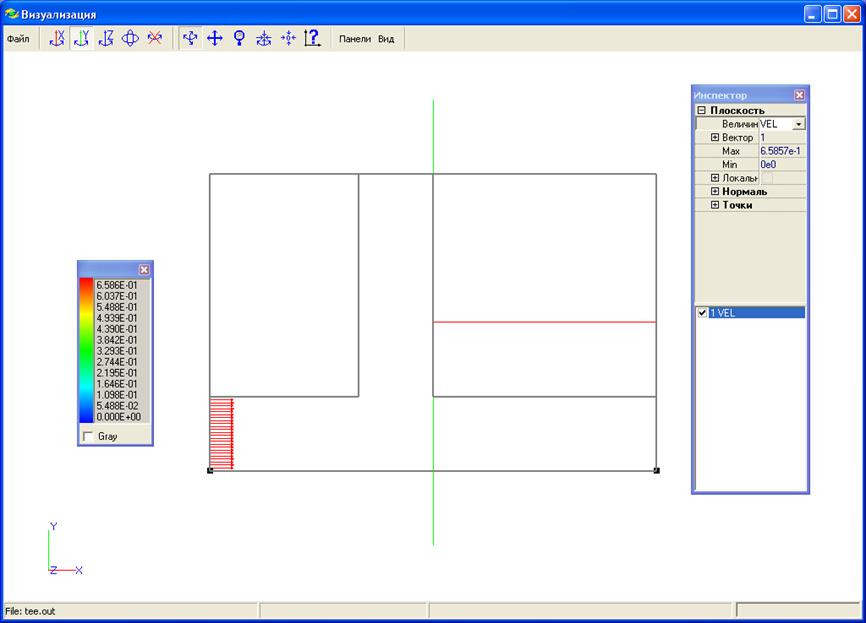
Рис.23. Блок визуализации программы SigmaFlow

Нажимаем на левую кнопку мышки в окне “Инспектор” и выбираем “Доб. Z”, после этого в среднем сечении тройника появится плоскость, перпендикулярная оси Z. В окне “Величины” инспектора выбираем “VEL”, теперь мы имеем возможность посмотреть, заданную нами скорость на входе в тройник (рис.23). Аналогичным образом выбираем “RHO” и “VISE” и смотрим, верно ли мы задали плотность и вязкость. Убедились в том, что все задано правильно, теперь можно приступать к расчету.

Закрываем блок визуализации и нажимаем кнопку “Расчет”. Снова появляются окна Nsimulation и Graff (рис.24). В окне Nsimulation можно найти информацию о выбранных математических моделях параметрах расчета (выбранные схемы аппроксимации, количество внутренних итераций, коэффициенты релаксации и др.) и текущем состоянии расчета (рис.12). В окне Graff представлены графики сходимости решения всех рассматриваемых нами дифференциальных уравнений (рис.25). В закладке “Residuals” находятся графики сходимости для трех компонент вектора скорости “U”,“V”,“W”. В закладке “Mass balance checks” графики сходимости решения уравнения на поправку давления “P” величина дивергенции скорости “div(V)” и некоторые другие расходные характеристики. В данном случае видно, что для получения решения достаточно около 700 итераций.

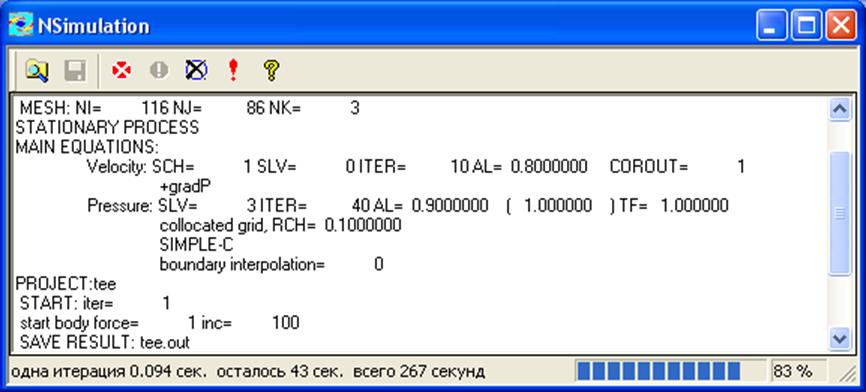
Рис.24. Окно с информацией о параметрах расчета

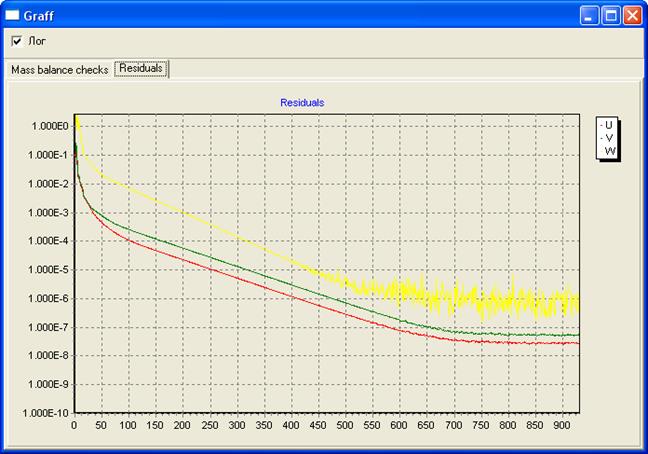
Рис. 25. Графики сходимости решения уравнений на компоненты скоростей

После достижения сходимости закрываем окно Nsimulation и преступаем к анализу результатов расчета. Нажимаем на кнопку “Анализ” и заходим в блок визуализации. В панели “Инспектор” создаем сечения расчетной области по Z и. Выбираем для просмотра в окне “Величина” вектор скорости “VEL”. В окне “Вектор” увеличиваем в два раза масштаб стрелок, которыми отображается поле скоростей (рис.26). Аналогичным образом можно посмотреть распределения поля давления и других величин (рис. 27).

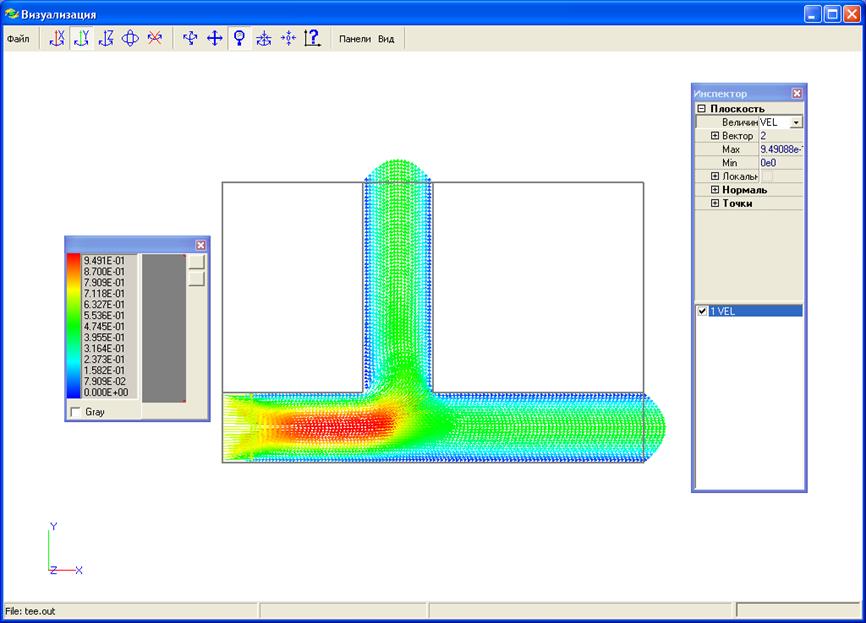
Рис. 27. Поле скоростей в тройнике при Re=10

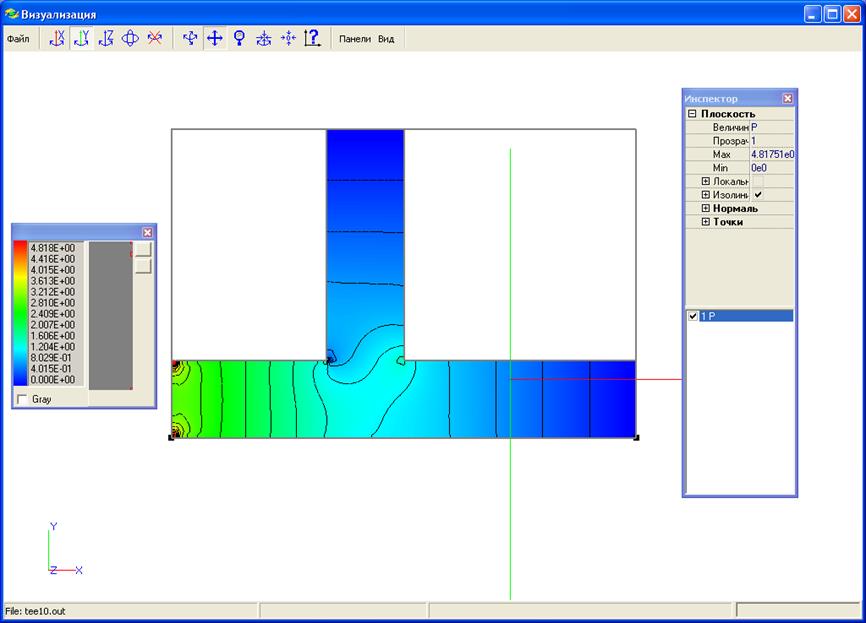
Рис. 28. Поле давления в тройнике при Re=10

Еще более наглядную визуализацию течения можно получить, используя визуализацию частицами. Для этого в меню “Панели” выбираем “Частицы”, в появившемся окне нажимаем правую кнопку мыши и выбираем “Добавить”. В строке “Вид” вместо “Частицы” выбираем “Треки”, в окне “Колл” ставим количество частиц равное 500. Устанавливаем временной шаг равным 0,2 и нажимаем кнопку ”Пуск”. Визуализация траекториями частиц представлена на рисунке 29.

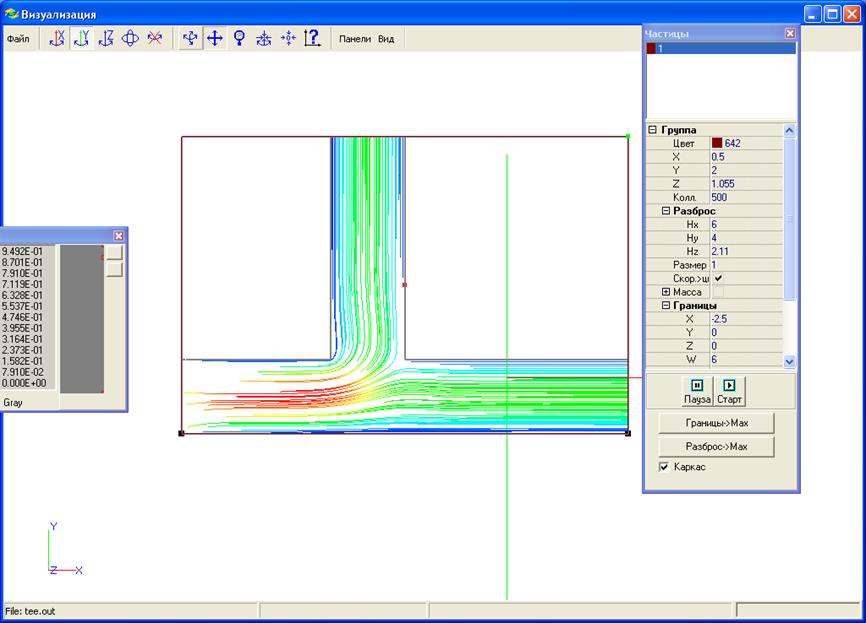
Рис 29. Визуализация течения частицами

Для того чтобы посмотреть распределение расхода по окнам тройника, необходимо в папке проекта открыть файл tee.log. В таблице “MASS FLUX:” (рис.30) в первом столбце находятся номера окон, которые мы присвоили на этапе построения геометрии, во втором массовые расходы через эти окна (кг/с). При этом если поток входит в объект то его значение считается положительным, если выходит то отрицательным. Так, например, смотрим в таблицу, номер входа у нас был равен 2, значение расхода через вход 0,667 кг/с. Верхний выход имел номер 3, расход через него 0,35кг/с. Боковой выход - 4, расход- 0,317.  

Рис.30. Массовые расходы через окна тройника

Меняя вязкость среды, аналогичным образом проводим расчеты для остальных чисел Рейнольдса. Результаты расчетов представлены в таблице 2 и на рисунках 31-35. Для удобства анализа рекомендуем сохранять результаты расчетов. Для этого в закладке “Файлы проекта” в окне “Выходные данные” изменим название файла tee.out например на teRe100.out.

Результаты расчетов

Таб.2 Массовые потоки

Re	10	100	200	300	400
Массовый расход  на входе, кг/с	0.668	0.668	0.668	0.668	0.668
Массовый расход на верхнем выходе, кг/с	0.35	0.4785376	0.532	0.55493	0.57040
Массовый расход на боковом выходе, кг/с	0.316	0.188462	0.135	0.11206	0.0965
Доля массового расхода на верхнем выходе, кг/с	0.524	0.717	0.7976	0.83	0.85
Доля массового расхода на верхнем выходе, кг/с (Эксперимент)	0.524	0.720	0.832	0.886	0.914

а)

б)

Рис 31. а) Траектории частиц маркеров. б) Поле давления. Число Рейнольдса 10

а)

б)

Рис 32. а) Траектории частиц маркеров. б) Поле давления. Число Рейнольдса 100

а)

б)

Рис 33. а) Траектории частиц маркеров. б) Поле давления. Число Рейнольдса 200

а)

б)

Рис 34. а) Траектории частиц маркеров.  б) Поле давления. Число Рейнольдса 300.

а)

б)

Рис 35. а) Траектории частиц маркеров. б) Поле давления. Число Рейнольдса 400.

В качестве задания к данной работе необходимо провести изучение влияния детализации расчетной сетки и выбора схемы аппроксимации на точность определения интегральных характеристик течения в тройнике. Определить гидродинамическое сопротивление верхнего и бокового рукавов тройника.  Все расчеты провести для чисел Рейнольдса 10 и 300. Полученные результаты сопоставить с экспериментальными данными из таблицы 2. Оформить отчет о проделанной работе.

Контрольные вопросы

1.  Дать определение гидродинамического сопротивления.  

2.  Что происходит с течением в тройнике при увеличении числа Рейнольдса?

3.  Как меняется сопротивление рукавов тройника при увеличении числа Рейнольдса?

4.  Почему при повышении числа Рейнольдса меняется распределение расходов жидкости через рукава тройника?

5.  Как влияет детализация расчетной сетки на точность определения интегральных характеристик течения в тройнике?

6.  Как влияет увеличение числа Рейнольдса на скорость сходимости задачи?

Библиографический список

1. FLUENT 6.0 Tutorial Guide.Validation.
2. Ferziger J.H., Peric M. Computational Methods for Fluid Dynamics. Berlin: Springer Verlag, 2002. – с.
3. Лойцянский Л. Г. Механика жидкости и газа. М.: Наука, 1970. – 840 c.