Министерство Образования и науки РФ
Новосибирский Государственный Технический Университет
Кафедра
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В СРЕДЕ MATLAB
КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ НА ОСНОВЕ
БУТСТРЕП – ПОДХОДА (МЕТОДА)
Факультет: бизнеса
Группа: ФБИ - 23
Студент: Гаранин И.Д.
Майоров В.А.
Преподаватель: Наумов А. А.
Новосибирск 2005
%Среднее квадратическое отклонение
sigma = 1.5;
%Реальные параметры модели
N=6;
Q=[6 -4 -3 0.5];
%Точки и количества наблюдений
PLAN=[
0 16;
2.765 16;
7.235 16;
10 16;
]
%Генерация массива случайных чисел с заданным среднеквадратическим отклонением и нулевым матожиданием.
randn=randn(16,4)*sigma;
%Инициализация массива
Ymodel=zeros(16,4);
%Моделирование: получение модельных данных с объекта
for j=1:16
for i=1:4
Ymodel(j,i)=Q(1)+Q(2)*PLAN(i,1)+Q(3)*PLAN(i,1)^2+Q(4)*PLAN(i,1)^3+randn(j,i);
end
end
%Результат: значения смоделированной выходной переменной
Ymodel
%выдает среднее значение
a=mean(Ymodel)
for j=1:16
for i=1:4
Ymodel1(j,i)=Ymodel(j,i)-a(i);
end
end
Ymodel1
for j=1:16
for i=1:4
k=i+4*(j-1);
Yl(k)=Ymodel1(j,i);
end
end
Yl
hist(Yl)
PLAN =
0 16.0000
2.7650 16.0000
7.2350 16.0000
10.0000 16.0000
Ymodel =
5.3512 -15.8260 10.6066 162.7440
3.5016 -17.3372 10.4510 165.9112
6.1880 -17.5696 11.3186 164.4840
6.4315 -18.6747 10.3861 166.9217
4.2803 -16.9845 11.1694 166.7616
7.7864 -19.4304 7.5795 168.5386
7.7837 -16.3547 9.3535 166.8869
5.9436 -14.9908 9.1481 165.0346
6.4909 -18.4638 6.9770 166.5705
6.2620 -16.1392 9.7691 164.4863
5.7199 -15.5451 7.7985 165.9707
7.0887 -19.8167 11.5059 165.9277
5.1175 -19.5876 8.1755 166.0001
9.2748 -16.5694 10.1763 165.5232
5.7954 -18.0260 9.7122 167.6425
6.1709 -16.3912 8.0003 163.1890
a =
6.1991 -17.3567 9.5080 165.7870
Ymodel1 =
-0.8480 1.5307 1.0986 -3.0431
-2.6975 0.0195 0.9431 0.1242
-0.0112 -0.2129 1.8106 -1.3030
0.2324 -1.3180 0.8781 1.1346
-1.9189 0.3722 1.6615 0.9746
1.5872 -2.0737 -1.9285 2.7516
1.5846 1.0020 -0.1545 1.0999
-0.2556 2.3659 -0.3599 -0.7524
0.2918 -1.1071 -2.5309 0.7835
0.0628 1.2175 0.2612 -1.3007
-0.4792 1.8115 -1.7095 0.1837
0.8895 -2.4601 1.9979 0.1406
-1.0816 -2.2309 -1.3324 0.2130
3.0756 0.7873 0.6683 -0.2638
-0.4037 -0.6693 0.2042 1.8555
-0.0283 0.9655 -1.5077 -2.5980
Yl =
Columns 1 through 13
-0.8480 1.5307 1.0986 -3.0431 -2.6975 0.0195 0.9431 0.1242 -0.0112 -0.2129 1.8106 -1.3030 0.2324
Columns 14 through 26
-1.3180 0.8781 1.1346 -1.9189 0.3722 1.6615 0.9746 1.5872 -2.0737 -1.9285 2.7516 1.5846 1.0020
Columns 27 through 39
-0.1545 1.0999 -0.2556 2.3659 -0.3599 -0.7524 0.2918 -1.1071 -2.5309 0.7835 0.0628 1.2175 0.2612
Columns 40 through 52
-1.3007 -0.4792 1.8115 -1.7095 0.1837 0.8895 -2.4601 1.9979 0.1406 -1.0816 -2.2309 -1.3324 0.2130
Columns 53 through 64
3.0756 0.7873 0.6683 -0.2638 -0.4037 -0.6693 0.2042 1.8555 -0.0283 0.9655 -1.5077 -2.5980
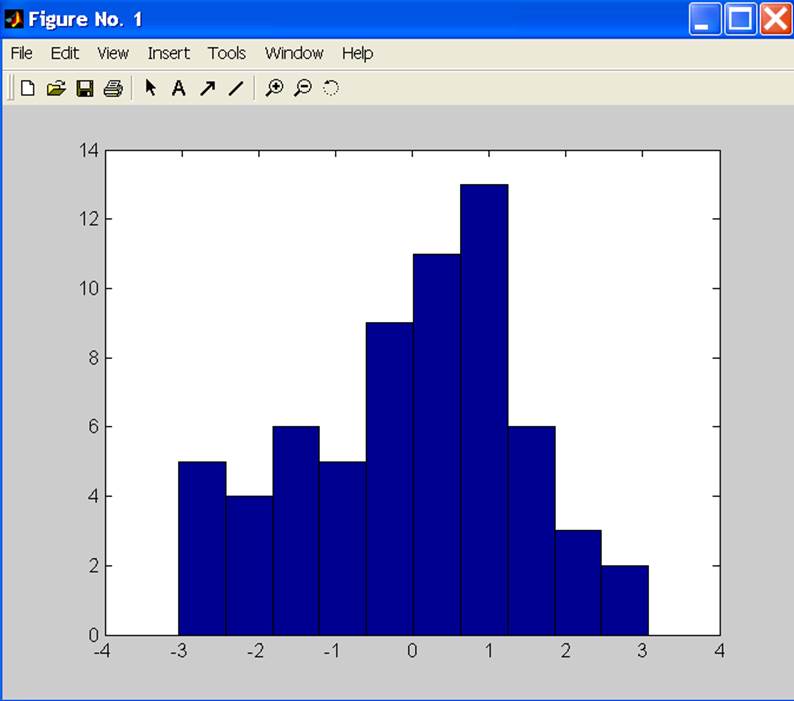
Рис. 1
sigma = 1.5;
%Реальные параметры модели
Q=[6 -4 -3 0.5];
X=[0:0.1:10];
SizeOfX=size(X);
k_int = 10
%Точки и количества наблюдений
PLAN=[
0 16;
2.765 16;
7.235 16;
10 16;
]
%Генерация массива случайных чисел с заданным среднеквадратическим отклонением и нулевым матожиданием.
random=randn(16,4)*sigma
%Инициализация массива
Ymodel=zeros(16,4);
%Моделирование: получение модельных данных с объекта
for j=1:16
for i=1:4
Ymodel(j,i)=Q(1)+Q(2)*PLAN(i,1)+Q(3)*PLAN(i,1)^2+Q(4)*PLAN(i,1)^3+random(j,i);
end
end
%Результат: значения смоделированной выходной переменной
Ymodel
Y=zeros(1,SizeOfX(2));
for i=1:SizeOfX(2)
Y(i)=Q(1)+Q(2)*X(i)+Q(3)*X(i)^2+Q(4)*X(i)^3;
end
for j=1:PLAN(1,2)
for i=1:4
e(j,i)=Ymodel(j,i)-Y(i);
end
end
k=0;
for j=1:PLAN(1,2)
for i=1:4
k=k+1;
elem(k)=e(j,i);
end
end
a=min(elem);
b=max(elem);
r_int=(b-a)/k_int;
for i=1:k_int
sum_n(i)=0;
end
for i=1:k
for j=1:k_int
if a + (j-1)*r_int <= elem(i) & elem(i) < a+j*r_int
sum_n(j)=sum_n(j)+1;
end
if elem(i)==b
sum_n(k_int)=sum_n(k_int)+1;
break
end
end
end
for i=1:k_int
p(i)=sum_n(i)/k;
end
max_p=max(p);
NI=PLAN(1,2);
for i=1:k_int
sum_b(i)=0;
end
NIC=NI;
for i=1:4
k=0;
while NI~=0
n_x=rand;
n_y=rand;
ran_x=a+(b-a)*n_x;
ran_y=max_p*n_y;
for j=1:k_int
if a + (j-1)*r_int <= ran_x & ran_x < a + j*r_int
if ran_y <= p(j)
if sum_b(j)<sum_n(j)
sum_b(j)=sum_b(j)+1;
k=k+1;
e_b(i,k)=ran_x;
NI=NI-1;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.