6.0888 -16.2601 10.9819 163.5222
5.1197 -17.1408 7.8966 166.5034
7.7729 -18.0997 8.9014 163.9780
5.3096 -17.2352 7.6208 166.4093
7.9773 -18.2365 10.7248 168.8782
4.1397 -17.3032 10.2841 164.6787
7.4922 -17.7366 9.0004 166.5097
6.9227 -16.5932 7.5252 165.0259
5.5793 -18.2443 7.6788 165.0293
3.9445 -15.5803 8.0816 170.7771
5.5234 -16.6379 9.8836 164.6498
MeanYB =
6.2709 -17.3659 9.3980 166.2209
MeanYall =
6.3311 -17.3624 9.4146 166.0496
Количество, когда Q_M > Q_MB:
sq_m =
51
Оценки параметров базовой модели, рассчитанные взвешенным МНК
Q_M =
6.3912
-4.2072
-2.9609
0.4977
Оценки параметров модели с учетом данных, сгенерированных бутстреп-методом, рассчитанные взвешенным МНК :
Q_MB =
6.3311
-4.1517
-2.9772
0.4990
В результате выполнения программы получили, что в большинстве просчетов из 100 оценки параметров модели после проведения компьютерных экспериментов с бутстреп выборкой оказались ближе к истинным параметрам. Это означает, что использование бустреп подхода позволяет улучшить характеристики оценки модели.
4. Проанализировать, как изменяются оценки параметров модели от средне квадратического отклонения ошибки наблюдения (Sigma).
Для анализа оценки параметров модели от среднеквадратического отклонения ошибки наблюдения. Используем следующие характеристики
- ![]() - наибольшее значение среди
наибольших на X разностей
- наибольшее значение среди
наибольших на X разностей ![]() за
100 модельных просчетов при определенном значении
за
100 модельных просчетов при определенном значении ![]() ;
;
- ![]() - среднее значение наибольших
на X разностей
- среднее значение наибольших
на X разностей ![]() за
100 модельных просчетов при определенном значении
за
100 модельных просчетов при определенном значении ![]() ;
;
- ![]() - среднее значение среди
наименьших на X разностей
- среднее значение среди
наименьших на X разностей ![]() за
100 модельных просчетов при определенном значении
за
100 модельных просчетов при определенном значении ![]() ;
;
- ![]() - наименьшее значение среди
наименьших на X разностей
- наименьшее значение среди
наименьших на X разностей ![]() за
100 модельных просчетов при определенном значении
за
100 модельных просчетов при определенном значении ![]() ;
;
- ![]() - среднее значение наибольших
на X разностей
- среднее значение наибольших
на X разностей ![]() за
100 модельных расчетов при определенном значении
за
100 модельных расчетов при определенном значении ![]() ;
;
- ![]() - среднее значение среди
наименьших на X разностей
- среднее значение среди
наименьших на X разностей ![]() за
100 модельных просчетов при определенном значении
за
100 модельных просчетов при определенном значении ![]() ;
;
X1=[0:0.1:10];
N=16;
PLAN=[
0 N;
2.765 N;
7.235 N;
10 N;
];
s1=1;
step=0.5;
s2=10;
kol=20;
n=4;
m=1;
Xplot=[];
E=[];
Eot=[];
Emin=[];
Emax=[];
ESmax=[];
ESmin=[];
ESmaxOt=[];
ESminOt=[];
for sigma=s1:step:s2
for ny=1:kol
random=randn(20,4)*sigma;
X=zeros(1,m);
f=[1 X(1) X(1)^2 X(1)^3];
k=4;
F=ones(n,k);
for i=1:n
for j=1:m
X(j)=PLAN(i,j);
end
f=[1 X(1) X(1)^2 X(1)^3];
for j=1:k
F(i,j)=f(j);
end
end
M=zeros(n,n);
for i=1:n
for j=1:m
X(j)=PLAN(i,j);
end
f=[1 X(1) X(1)^2 X(1)^3];
f=f';
M = M+ PLAN(i,m+1)*f*f';
end
Y=[];
for i = 1:n
ransr=0.;
for j=1:PLAN(i,m+1)
rnd(j)=random(j);
%rnd(j) = randn()*sigma;
ransr = ransr + rnd(j);
end
ransred(i)=ransr/PLAN(i,m+1);
dispers1 = 0.;
for j=1:PLAN(i,m+1)
dispers1 = dispers1 +(rnd(j)-ransred(i))^2;
end
dispers(i)= dispers1/((PLAN(i,m+1)-1)*PLAN(i,m+1));
end
D2 = diag(dispers);
Mwave = inv((F'*inv(D2))*F);
iM=inv(M);
x1servis=0;
sizeX1=size(X1);
while x1servis<sizeX1(2),
x1servis=x1servis+1;
p1=X1(x1servis);
f=[1 p1 p1^2 p1^3];
Disp(ny,x1servis) = f*Mwave*f';
Dispc1(x1servis) = sigma^2*f*iM*f';
end
end
for i=1:kol
for j=1:size(X1,2)
E(i,j)=abs(Dispc1(j)-Disp(i,j));
Eot(i,j)=abs((Dispc1(j)-Disp(i,j))/Dispc1(j));
end
end
Emax=[Emax;max(max(E))];
Emin=[Emin;min(min(E))];
ESmax=[ESmax;mean(max(E))];
ESmin=[ESmin;mean(min(E))];
ESmaxOt=[ESmaxOt;mean(max(Eot))];
ESminOt=[ESminOt;mean(min(Eot))];
Xplot=[Xplot;sigma];
end
%plot(Xplot,Emax,'m-',Xplot,ESmax,'k--',Xplot,ESmaxOt,'c.--');
plot(Xplot,Emin,'r-',Xplot,ESmin,'b--',Xplot,ESminOt,'g.--');
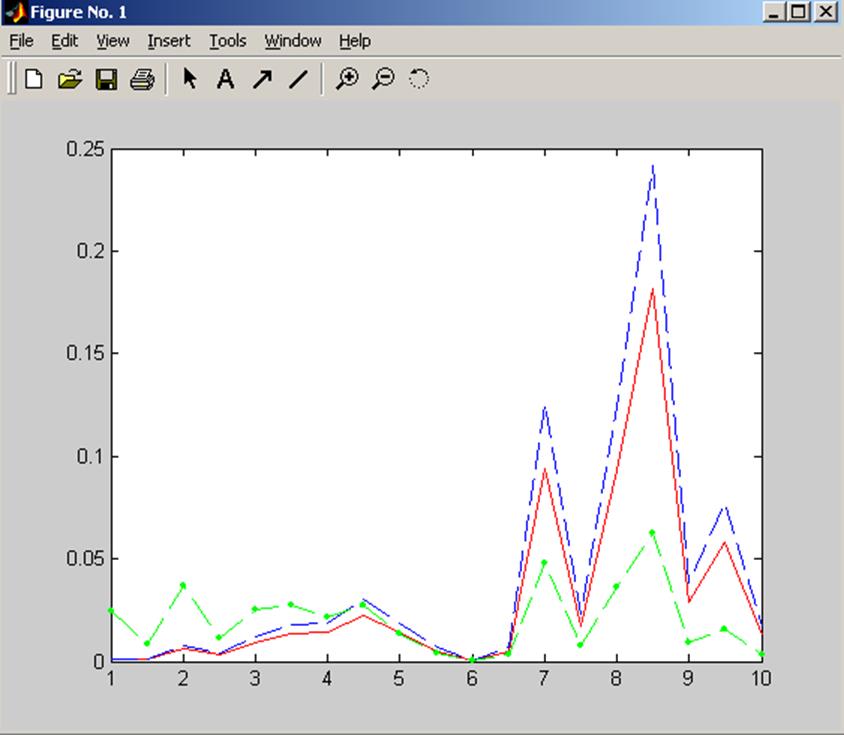
Рис. 2.
Красная сплошная линия – ![]()
Синяя пунктирная линия – ![]()
Зеленая линия точка-тире - ![]()
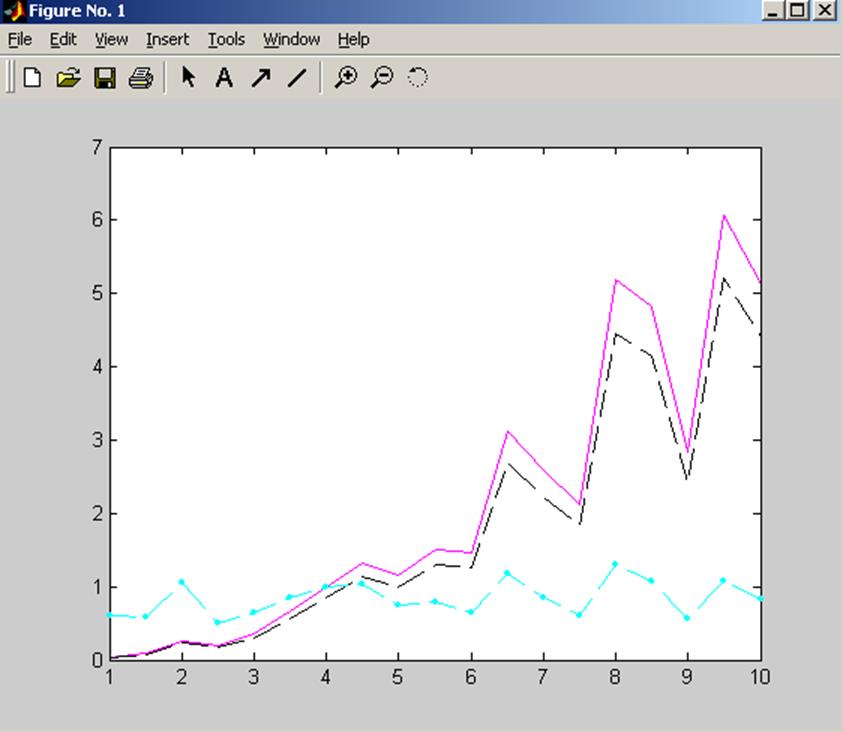
Рис. 3.
Красная линия - ![]()
Синяя пунктирная линия – ![]()
Зеленая линия точка-тире - ![]()
Из графиков видно, что с увеличением значения σ увеличивается разница между значениями априорной и апостериорных дисперсий оценок функции отклика. Таким образом, чем меньше значение σ, тем ближе моделируемые данные к истинным параметрам заданной модели.
5. Выводы
В результате проделанной работы можно сказать, что полученные оценки параметров модели после проведения компьютерных экспериментов стали ближе к истинным параметрам, чем оцененные непосредственно после проведения реальных экспериментов. Данный факт говорит об эффективности использования бутстреп-метода для улучшения характеристик стратегии экспериментирования. Необходимо отметить, что для получения данных, максимально приближенных к заданной модели, необходимо сократить разброс шума, т.е. среднеквадратического отклонения, практически до нуля.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.