Решение задач финансовой математики с помощью встроенных финансовых функций методом прямого счета

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТА

ОТЧЕТ

по лабораторной работе №1

Факультет: Бизнеса

Группа: ФБИ-63

Студенты: Иванова И.Е.

                   Конов П.Н.

Преподаватель: Кириллов Ю.В.

Новосибирск

2009

Цель работы:

·  Приобрести практические навыки решения задач финансовой математики с помощью встроенных финансовых функций.

·  Научиться решать задачи методом прямого счета.

1. Расчет наращенных процентов

1.1 При постоянной процентной ставке (данные приведены в таблице

Задача. Определите, какая сумма окажется на счете, если вклад размером Р тыс. руб. положен под   j %  годовых на  n  лет, а проценты начисляются ежеквартально?

Таблица 1

Номер бригады	P, тыс. руб	n ,лет	j, %
4	1200	22	12

Решение. Для того чтобы найти наращенную сумму, используем формулу сложных процентов:

  

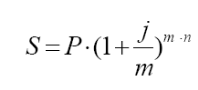
где n – число лет;

j – номинальная процентная ставка;

P – приведенная стоимость;

S – наращенная сумма;

m – число начислений процентов в году

Решаем задачу в Excel, используя встроенную функцию БС, которая возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки. Синтаксис: БС (Ставка; Число периодов; Выплата; НЗ; Тип)

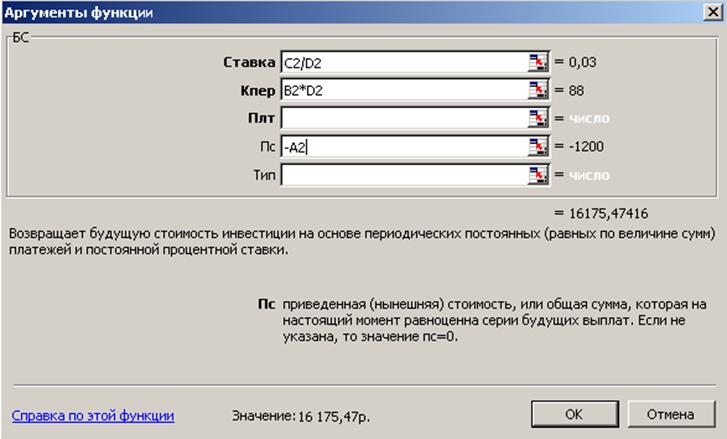
Рис.1

Решаем задачу методом прямого счета (см. рис. 2), построив в Excel электронную формулу для расчета наращенной суммы по математической формуле (1).

Рис.2

Вывод: при сравнении результата для расчета наращенной суммы, который получен методом прямого счета и при использовании встроенной функции БС отметим, что они совпадаю. Следовательно, задача решена верно.

  1.2 При переменной процентной ставке

Задача. Рассчитать будущую стоимость облигации номиналом Р тыс. руб., если предусмотрен следующий порядок начисления процентов: в первые  n₁  лет – i₁ %  годовых, в следующие n₂  лет -  i₂ %  и в последние n₃  лет -  i₃ % годовых.

Таблица №2

Номер бригады	P, тыс. руб.	n1, лет	n2, лет	n3, лет	j1 ,%	j2 ,%	j3 ,%
4	130	2	3	1	5	4	7

Решение. Для того, чтобы найти будущую стоимость облигации используем формулу:

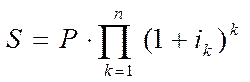
S – наращенная сумма;

P – стоимость облигации;

i – годовая процентная ставка

n – число лет;

Решаем задачу в Excel, используя встроенную функцию БЗРАСПИС:

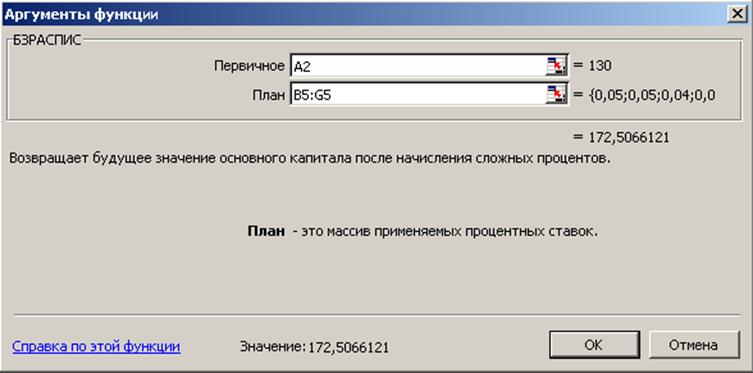
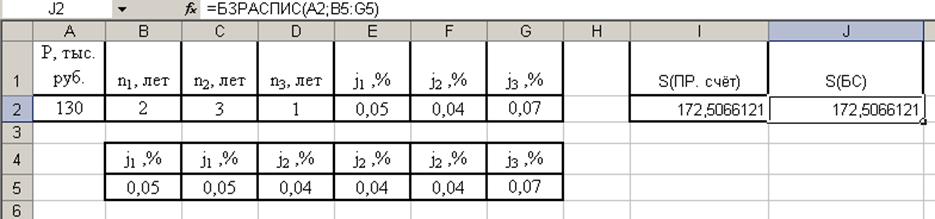Рис.3

Решаем задачу методом прямого счета (см. рис. 4), построив в Excel электронную формулу для расчета наращенной суммы по математической формуле (2).

Рис. 4

Вывод: при сравнении результата для расчета наращенной суммы, который получен методом прямого счета и при использовании встроенной функции БЗРАСПИС отметим, что они совпадаю. Следовательно, задача решена верно.

2.  Расчет приведенной стоимости

2.1 Для постоянного потока платежей

Задача. Какую сумму необходимо положить на депозит под  j %  годовых, чтобы получить через  n  лет  Sтыс. руб., при полугодовом начислении процентов?

Таблица №3

Номер бригады	S, тыс. руб.	n, лет	m, число начислений	j ,%
4	47	4	2	12

Решение.

Для поиска необходимой суммы воспользуемся формулой приведённой суммы для однократного вклада (3):

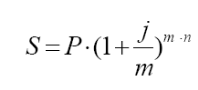
Решение задачи с помощью функции ПС:

S – наращенная сумма;

Р – приведенная стоимость;

j – начисляемы проценты;

n – число лет;

m – число начислений процентов в году

Решаем задачу в Excel, используя встроенную функцию ПС:

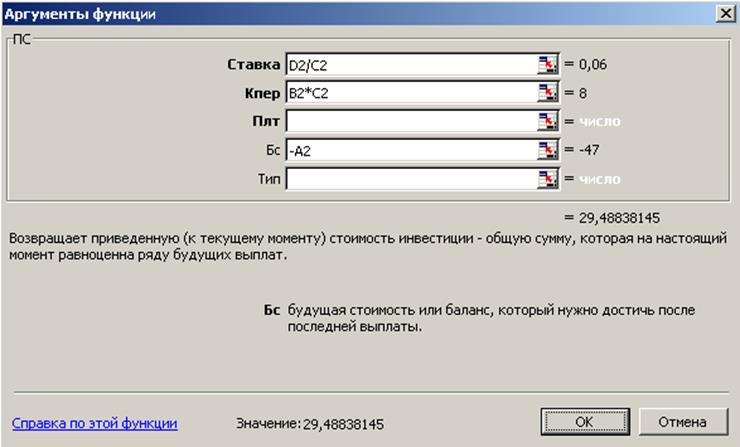
Рис. 5

Решаем задачу методом прямого счета (см. рис. 6), построив в Excel электронную формулу для расчета приведенной суммы по математической формуле (3).

Рис.6

Вывод: при сравнении результата для расчета приведенной суммы, который получен методом прямого счета и при использовании встроенной функции ПС отметим, что они совпадаю. Следовательно, задача решена верно.

2.2 Для переменного потока платежей

Задача. Капитальные затраты по проекту составляют  Kтыс. руб. и ожидается, что его реализация принесет доходы за три года:  D₁тыс. руб., D₂тыс. руб. и  D₃тыс. руб. соответственно. Издержки привлечения капитала равны i % . Определить  чистую текущую стоимость проекта.

Номер бригады	K, тыс. руб.	D1, тыс. руб.	D2, тыс. руб.	D3, тыс. руб.	i ,%
4	130	2	3	1	5

Таблица №4

Решение. Воспользуемся формулой для расчёта регулярных потоков платежей (4):

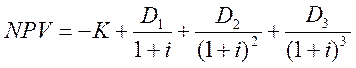
Решаем задачу с помощью функции ЧПС:

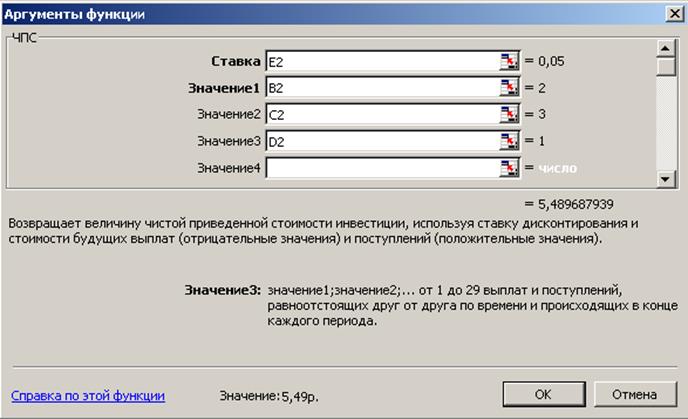
Рис. 7

Решаем задачу методом прямого счета (см. рис. 6), построив в Excel электронную формулу для расчета чистой текущей стоимости проекта по математической формуле (4).

Рис.8

Вывод: при сравнении результата для расчета потока регулярных платежей, который получен методом прямого счета и при использовании встроенной функции ЧПС отметим, что они совпадаю. Следовательно, задача решена верно.

2.3 Для не регулярного поток платежей

Задача. Определите чистую приведенную стоимость инвестиций, если 27.12.2002 предполагается выплата  Kтыс. руб., а поступления составят 20.06.2003 - D₁тыс. руб., 12.12.2003 - D₂тыс. руб. и 17.07.2004 - D₃тыс. руб., если ставка процента – i %  годовых.

Таблица №5

Номер бригады	K, тыс. руб.	D1, тыс. руб.	D2, тыс. руб.	D3, тыс. руб.	i ,%
4	8	1,9	4,7	5,2	11

Решение: воспользуемся формулой для не регулярных платежей(5):

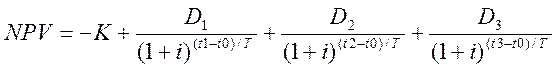
Решаем задачу с помощью функции ЧИСТНЗ:

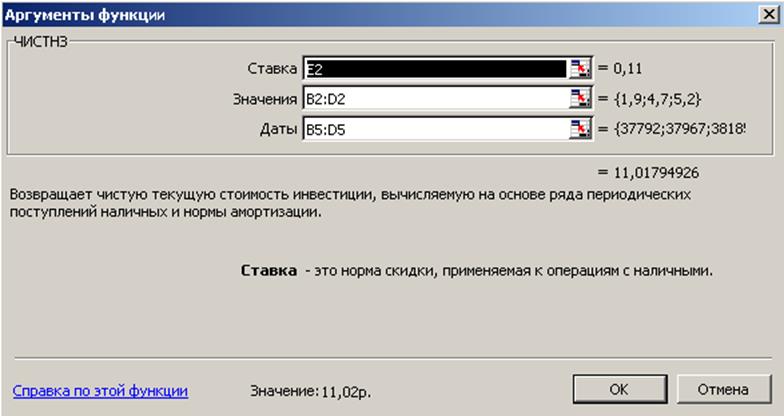
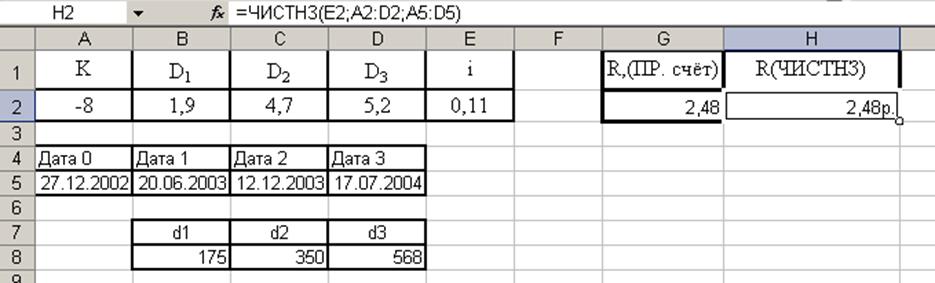
Рис.9

Решаем задачу методом прямого счёта:

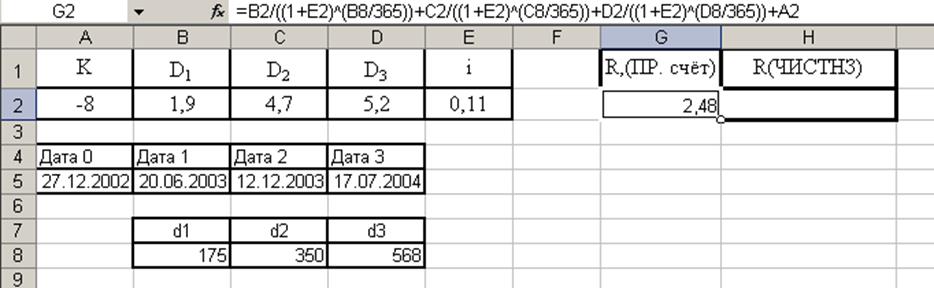
Рис.10

Вывод: при сравнении результата для расчета потока регулярных платежей, который получен методом прямого счета и при использовании встроенной функции ЧИСТНЗ отметим, что они совпадаю. Следовательно, задача решена верно.

3.  Определение срока платежа и процентной ставки

3.1 Срок постоянного потока платежей

Задача. Сколько лет потребуется, чтобы платежи размером  R тыс. руб. в конце каждого года достигли значения  Sтыс. руб., если начисление процентов ежегодное по ставке -  i %

Номер бригады	S, тыс. руб.	R, тыс. руб.	j ,%
4	15,2	2,4	12,3

Воспользуемся формулой для расчёта наращенной суммы ежегодной ренты с ежегодным начислением процентов(6):

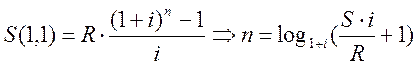
Решение задачи с помощью функции КПЕР:

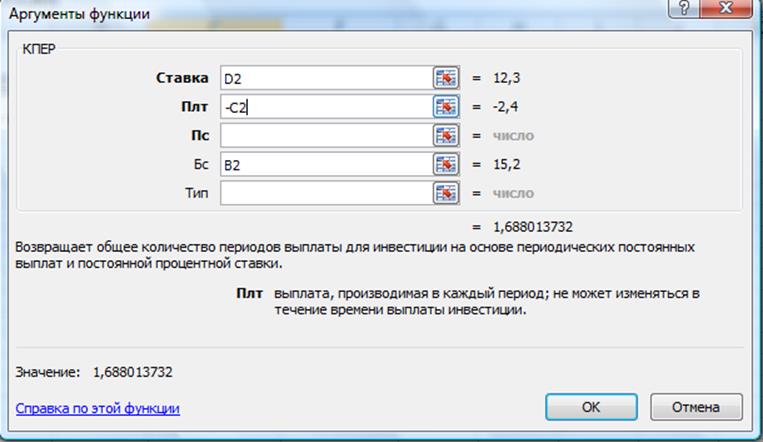
Рис. 11

Решаем задачу методом прямого счёта:

Рис. 12

Вывод: при сравнении результата для расчета срока платежа, который получен методом прямого счета и при использовании встроенной функции КПЕР отметим, что они совпадаю. Следовательно, задача решена верно.

3.2. Процентная ставка

Задача. Рассчитать годовую ставку процента по вкладу размером  Pтыс. руб., если за  n  лет эта сумма выросла до  Sтыс. руб., при ежеквартальном начислении процентов.

Таблица №7

Формула для расчёта (метод прямого счёта):

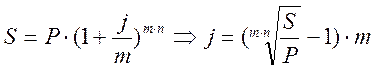
Решение задачи с помощью функции СТАВКА:

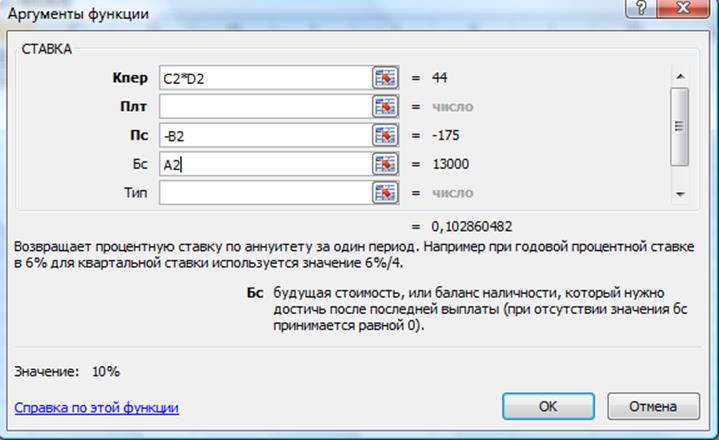
Рис.13

Решение методом прямого счёта:

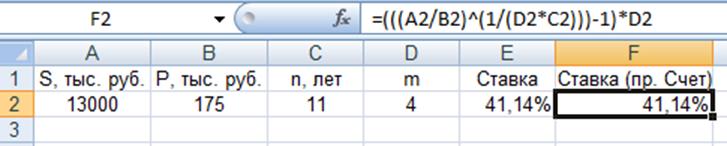
Рис.14

Вывод: при сравнении результата для расчета процентной ставки, который получен методом прямого счета и при использовании встроенной функции СТАВКА отметим, что они совпадаю. Следовательно, задача решена верно.

4.  Расчет эффективной процентной ставки и размера платежа.

Задача. Облигация номиналом  P тыс. руб. выпущена на n лет при номинальной ставке – j %. Рассчитайте эффективную ставку при начислении процентов m  в год.

Таблица.№8

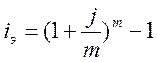
Решение задачи методом прямого счёта:

Рис.15

Решение задачи с использованием функции ЭФФЕКТ:

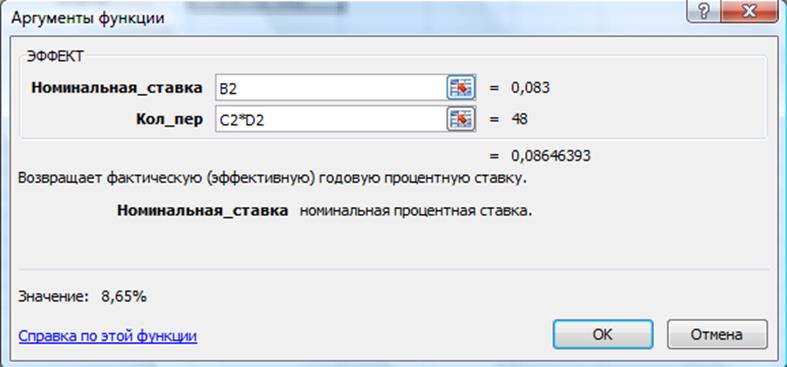
Рис.16

Вывод: при сравнении результата для расчета эффективной процентной ставки, который получен методом прямого счета и при использовании встроенной функции ЭФФЕКТ отметим, что они совпадают. Следовательно, задача решена верно.

5.  Размер платежа постоянной ренты.

Задача. Необходимо накопить Sтыс. руб. за  n  лет, откладывая постоянную сумму в конце каждого квартала. Какова должна быть эта сумма, если номинальная ставка – j %, а начисление ежеквартальное?

Таблица №9

Воспользуемся формулой ежегодной ренты с ежеквартальным начислением процентов:

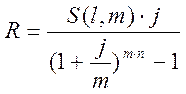
Метод прямого счёта:

Рис.17

Использование функции ПЛТ:

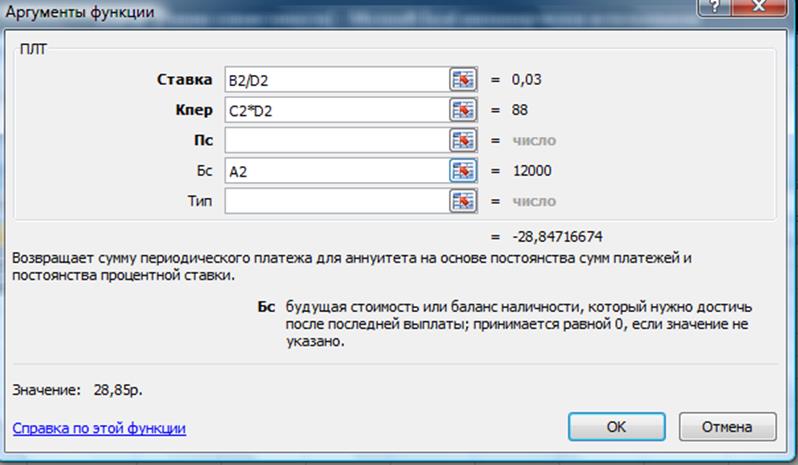
Рис.18

Результаты совпадают.

Вывод. при сравнении результата для расчета размера платежа постоянной ренты, который получен методом прямого счета и при использовании встроенной функции ПЛТ отметим, что они совпадают. Следовательно, задача решена верно.