Решение задач финансовой математики с помощью встроенных финансовых функций

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Новосибирский Государственный Технический Университет

Кафедра экономической информатики

Лабораторная работа №1

Вариант 8

Факультет: Бизнеса

Группа: ФБИ-71

Студентки: Габова Л.А.

                    Хуторненко В.А.

Проверил: Кириллов Ю.В.

Новосибирск ,  2010

Цель работы:

• Приобрести практические навыки решения задач финансовой математики с помощью встроенных финансовых функций.
• Научиться решать задачи методом прямого счета.

1.  Задание к лабораторной работе 1:

.1.  Расчёт наращенной суммы:

.1.1.  При постоянной процентной ставке (данные приведены в таблице 1):

Задача. Какая сумма должна быть выплачена, если n лет назад была выдана ссуда P тыс. руб. под j % годовых с ежемесячным начислением процентов?

Таблица 1

№ бригады	P, тыс.руб.	n, лет	i (j), %
8	1700	8	13

Решение. Для того, чтобы найти наращенную сумму используем формулу сложных процентов:

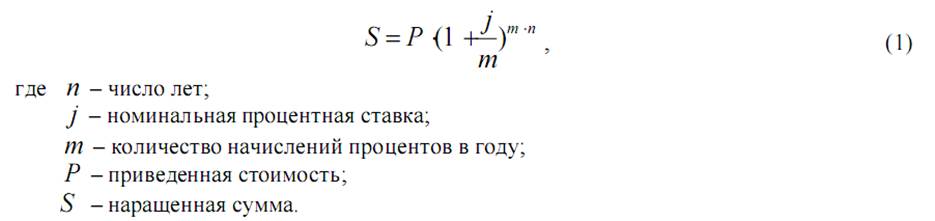
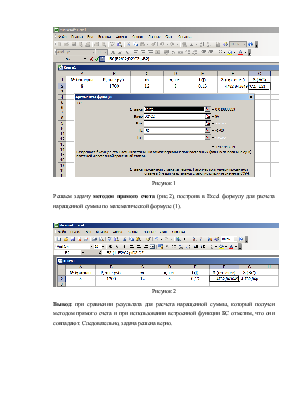
Решаем задачу в Excel, используя встроенную функцию  БС (рис.1), которая возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки. Синтаксис: БС (Ставка; Число периодов; ;НЗ;).

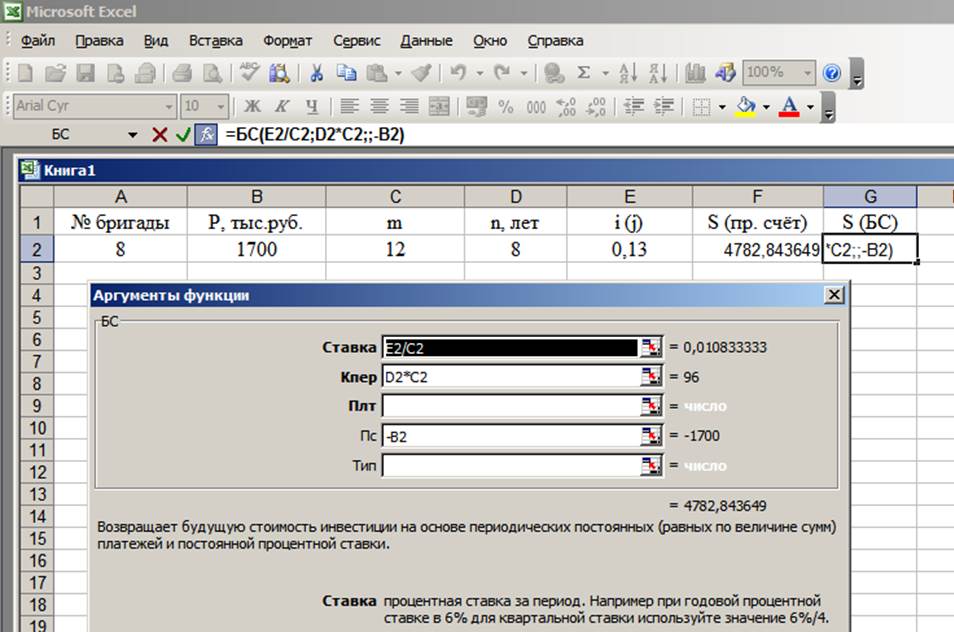
Рисунок 1

Решаем задачу методом прямого счета (рис.2), построив в Excel формулу для расчета наращенной суммы по математической формуле (1).

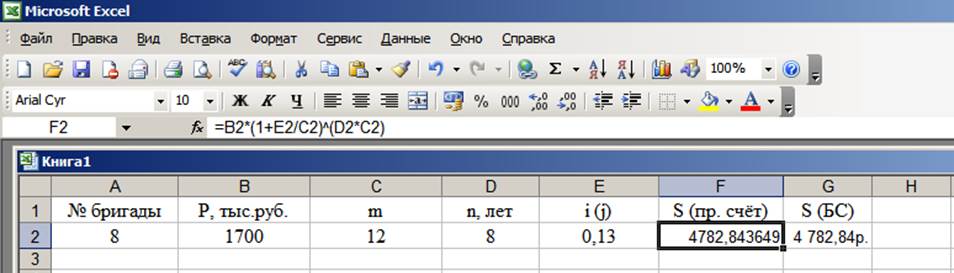
Рисунок 2

Вывод: при сравнении результата для расчета наращенной суммы, который получен методом прямого счета и при использовании встроенной функции БС отметим, что они совпадают. Следовательно, задача решена верно.

.1.2.  При переменной процентной ставке (данные приведены в таблице 2):

Таблица 2

№ бригады	P, тыс.руб.	n1, лет	n2, лет	i1 %	i2 %
8	170	2	3	6	5

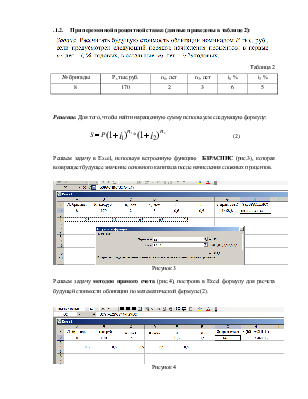
Решение. Для того, чтобы найти наращенную сумму используем следующую формулу:

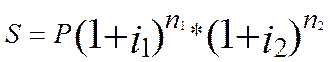                                               (2)

Решаем задачу в Excel, используя встроенную функцию  БЗРАСПИС (рис.3), которая возвращает будущее значение основного капитала после начисления сложных процентов.

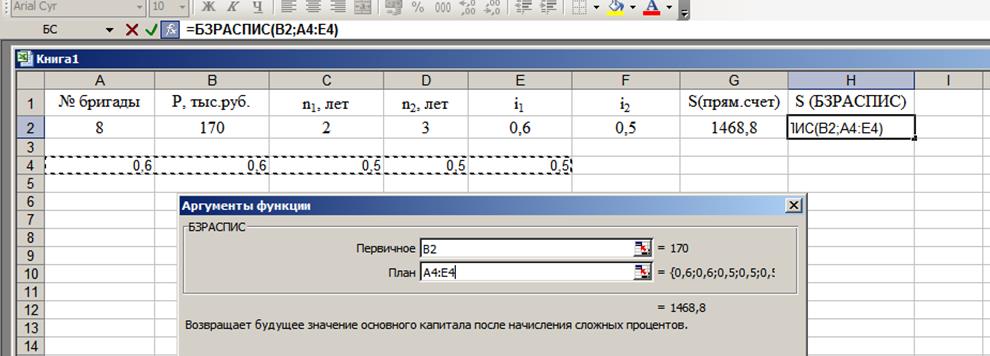
Рисунок 3

Решаем задачу методом прямого счета (рис.4), построив в Excel формулу для расчета будущей стоимости облигации по математической формуле (2).

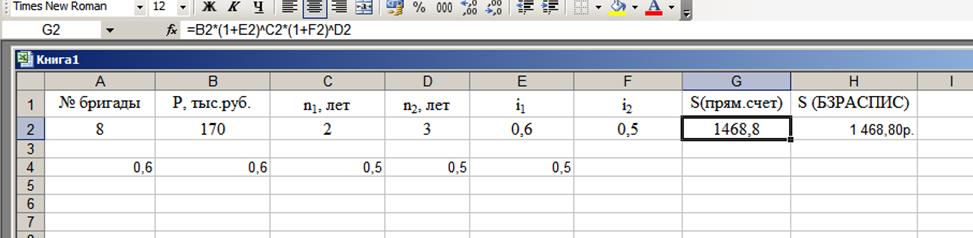
Рисунок 4

Вывод: при сравнении результата для расчета будущей стоимости облигации, который получен методом прямого счета и при использовании встроенной функции БЗРАСПИС отметим, что они совпадают. Следовательно, задача решена верно.

.2.  Расчёт приведённой стоимости.

.2.1.  Для постоянного потока платежей (данные приведены в таблице 3):

Таблица 3

№ бригады	R, тыс.руб.	n, лет	j %
8	140	6	9,5

Решение. Для того, чтобы рассчитать текущую стоимость обязательных ежемесячных платежей используем следующую формулу:

                           

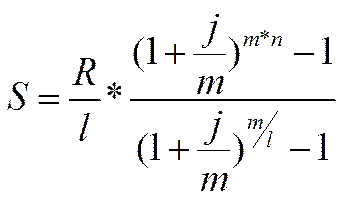
                                (3)

Решаем задачу в Excel, используя встроенную функцию  ПС (рис.5), которая возвращает приведённую стоимость обязательных платежей.

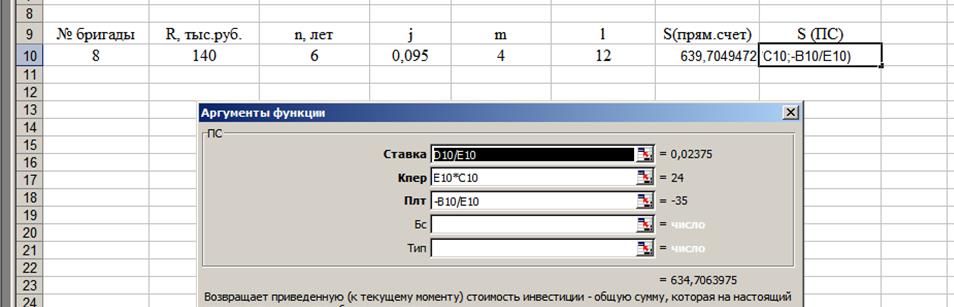
Рисунок 5

Решаем задачу методом прямого счета (рис.6), построив в Excel формулу для расчета приведённой стоимости обязательных платежей. по математической формуле (3).

Рисунок 6

Вывод: при сравнении результата для расчета приведенной стоимости обязательных платежей, который получен методом прямого счета и при использовании встроенной функции ПС отметим, что они незначительно отличаются, так как встроенная формула Excel может правильно рассчитать параметры периодических платежей, только если количество платежей в году равно количеству начислений процентов в году. Следовательно, задача решена верно.

.2.2.  Для переменного потока платежей (данные приведены в таблице 4):

Таблица 4

№ бригады	K, тыс.руб.	D1, тыс.руб.	D2, тыс.руб.	D3, тыс.руб.	D4, тыс.руб.	i %
8	120	15	22	34	40	17

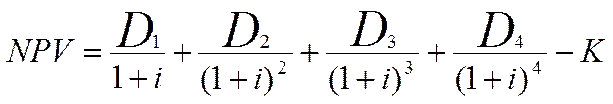Решение. Для того, чтобы рассчитать эффективность проекта используем следующую формулу:

(4)

Решаем задачу в Excel, используя встроенную функцию  ЧПС (рис.7), которая рассчитывает эффективность проекта.

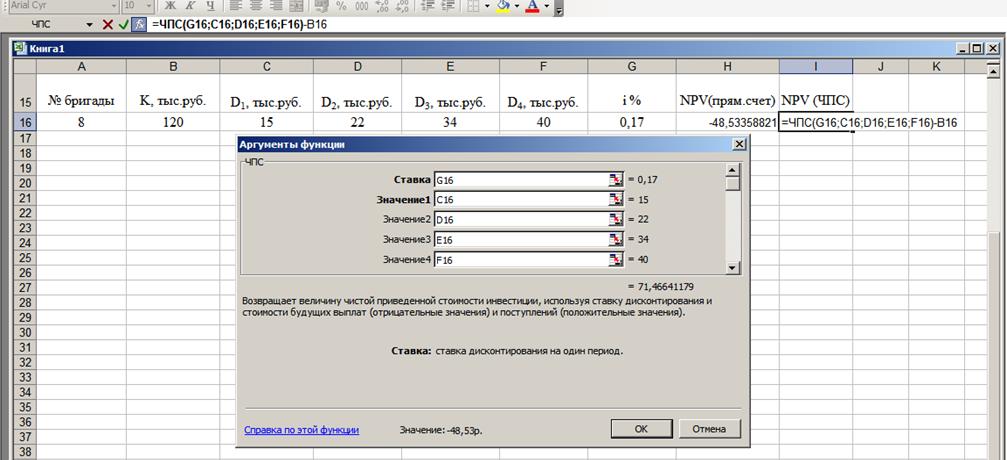
Рисунок 7

Решаем задачу методом прямого счета (рис.8), построив в Excel формулу для расчета эффективности проекта по математической формуле (4).

Рисунок 8

Вывод: при сравнении результата для расчета эффективности проекта, который получен методом прямого счета и при использовании встроенной функции ЧПС отметим, что они совпадают. Следовательно, задача решена верно.

.2.3.  Для нерегулярного потока платежей (данные приведены в таблице 5):

Таблица 5

№ бригады	K, тыс.руб.	D1, тыс.руб.	D2, тыс.руб.	D3, тыс.руб.	D4, тыс.руб.	i %
8	25	3,6	5,2	6,9	10,1	11

Решение. Для того, чтобы рассчитать чистую приведенную стоимость инвестиций используем следующую формулу:

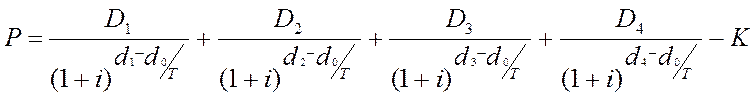
                (5)

Решаем задачу в Excel, используя встроенную функцию  ЧИСТНЗ (рис.9), которая рассчитывает чистую приведенную стоимость инвестиций.

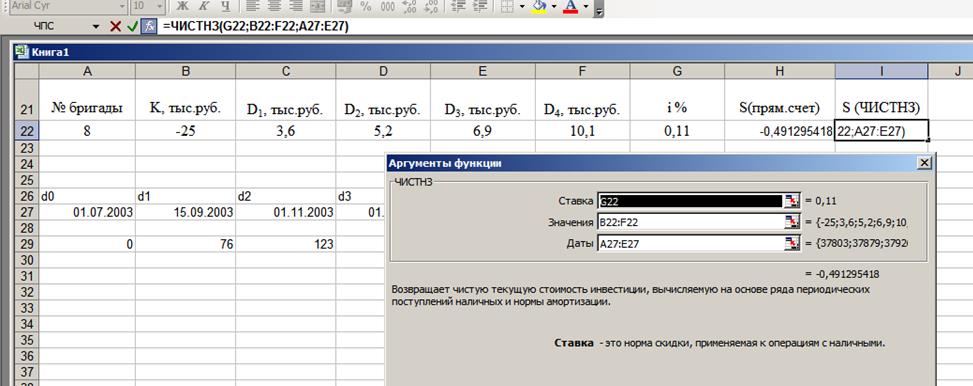
Рисунок 9

Решаем задачу методом прямого счета (рис.10), построив в Excel формулу для расчета чистой приведенной стоимости инвестиций по математической формуле (5).

Рисунок 10

Вывод: при сравнении результата для расчета чистой приведенной стоимости инвестиций, который получен методом прямого счета и при использовании встроенной функции ЧИСТНЗ отметим, что они совпадают. Следовательно, задача решена верно.

.3.  Определение срока платежа и процентной ставки:

.3.1.  Срок постоянного потока платежей (данные в таблице 6):

Таблица 6

№ бригады	S, тыс.руб.	P, тыс.руб.	i %
8	12200	320	12,8

Решение. Для того, чтобы рассчитать количество месяцев вклада используем следующую формулу:

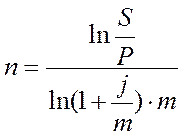
                                                          (6)

Решаем задачу в Excel, используя встроенную функцию  КПЕР (рис.11), которая рассчитывает срок вклада.

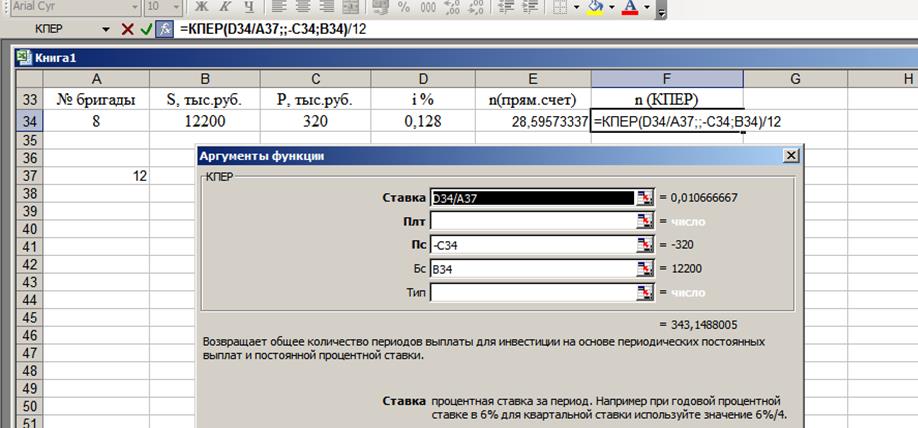
Рисунок 11

Решаем задачу методом прямого счета (рис.12), построив в Excel формулу для расчета срока вклада по математической формуле (6).

Рисунок 12

Вывод: при сравнении результата для расчета срока вклада, который получен методом прямого счета и при использовании встроенной функции КПЕР отметим, что они совпадают. Следовательно, задача решена верно.

.3.2.  Процентная ставка (данные в таблице 7):

Таблица 7

№ бригады	S, тыс.руб.	R, тыс.руб.	n, лет
8	23000	840	4

Решение. Для того, чтобы рассчитать годовую ставку процента используем следующую формулу:

                                                          (7)

Решаем задачу в Excel, используя встроенную функцию  СТАВКА (рис.13), которая рассчитывает процентную ставку.

Рисунок 13

Решаем задачу методом прямого счета (рис.14), построив в Excel формулу для расчета ставки процента по математической формуле (7).

Рисунок 14

Вывод: при сравнении результата для расчета ставки процента, который получен методом прямого счета и при использовании встроенной функции СТАВКА отметим, что они совпадают. Следовательно, задача решена верно.

.4.  Расчет эффективной ставки и размера платежа:

.4.1.  Эффективная ставка (данные в таблице 8):

Таблица 8

№ бригады	P, тыс.руб.	i %	m	n, лет
8	14000	9,6	12	4

Решение. Для того, чтобы рассчитать эффективную ставку процента используем следующую формулу:

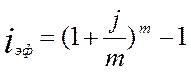
                                                          (8)

Решаем задачу в Excel, используя встроенную функцию  ЭФФЕКТ (рис.15), которая рассчитывает эффективную ставку процента.

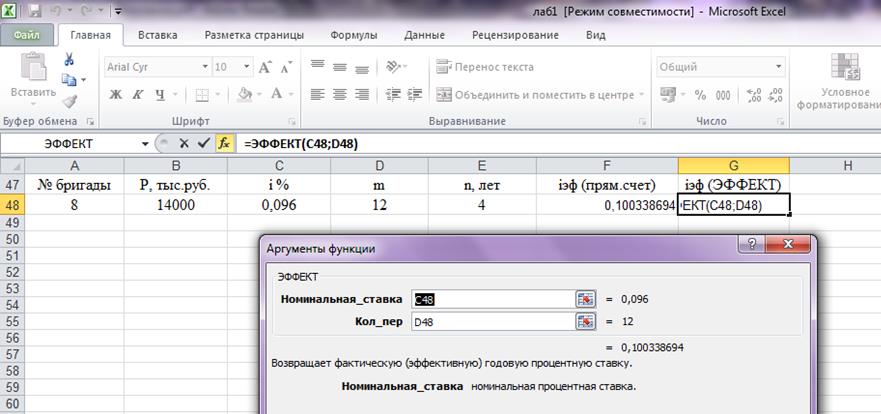
Рисунок 15

Решаем задачу методом прямого счета (рис.16), построив в Excel формулу для расчета эффективной ставки процента по математической формуле (8).

Рисунок 16

Вывод: при сравнении результата для расчета эффективной ставки процента, который получен методом прямого счета и при использовании встроенной функции ЭФФЕКТ отметим, что они совпадают. Следовательно, задача решена верно. Данные о количестве лет и сумме займа в расчетах не пригодились.

.4.2.  Размер платежа и постоянной ренты (данные в таблице 9):

Таблица 9

№ бригады	P, тыс.руб.	n, лет	j, %
8	1700	8	13

Решение. Для того, чтобы рассчитать эффективную размер платежа используем следующую формулу:

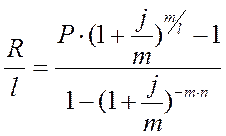                                                          (9)

Решаем задачу в Excel, используя встроенную функцию  ПЛТ (рис.17), которая рассчитывает размер платежа.

Рисунок 17

Решаем задачу методом прямого счета (рис.18), построив в Excel формулу для расчета размера платежа по математической формуле (9).

Рисунок 18

Вывод: при сравнении результата для расчета размера платежа, который получен методом прямого счета и при использовании встроенной функции ПЛТ отметим, что они совпадают. Следовательно, задача решена верно.