Значение атрибута – это экземпляр домена, каждая ячейка описывает сущность домена, например, qty_on_hand 2000 формально может рассматриваться как qty_on_hand: 2000. Указанное значение, например 2000 – это отображаемая часть; домен описывается заголовком столбца. Отметим, что заголовок столбца – это имя как атрибута, так и домена.
Специальный символ null показывает, что сущность не имеет значения этого атрибута; nill не принадлежит ни одному домену.
Рисунок показывает, что значение атрибута qty_on_hand сущности production part i1 – 2000. Аксиомы теории формализации позволяют записать это формально как предложение с частицей has (иметь). На рисунке показано предложение и терминология.
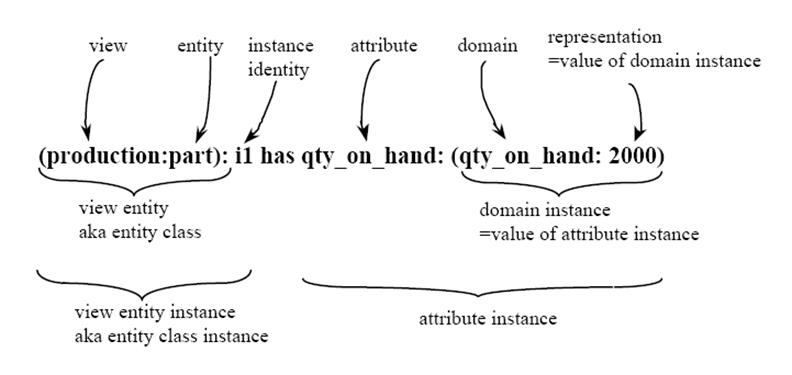
Пример связей сущностей для представления production TcCo показан ниже. Каждая таблица названа отношением и специфична для него. У каждой таблицы два столбца, названные именами участвующих сущностей. Каждая строка таблицы состоит из идентификаторов участвующих сущностей.
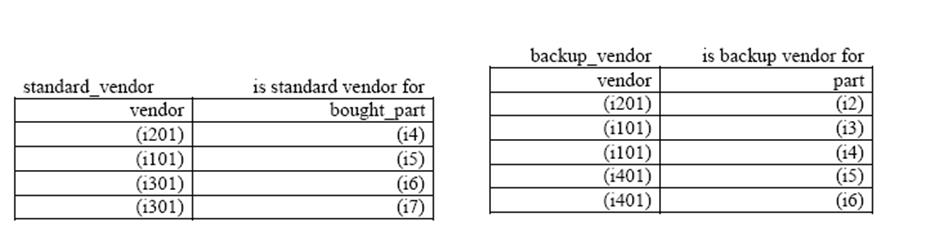
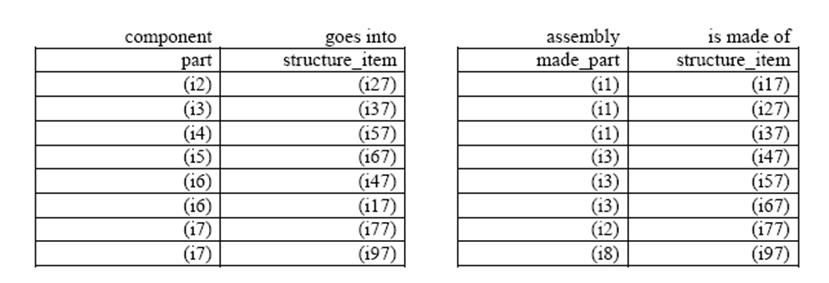
Первая таблица показывает, что деталь i4 поставляется вендором i201. Аксиомы теории формализации позволяют записать это формально как предложение с частицей has (иметь).
( production: bought_part ): i4 has ‘standard vendor’: i201.
Здесь ‘standard vendor’: i201 называется участвующим экземпляром, также это экземпляр класса, ссылающийся на значение участвующего экземпляра.
B.1.4 Язык логики первого порядка
Для формализации используется язык равноправной логики первого порядка. В этой секции описана используемая нотация.
B.1.4.1 Символы истинности
Используются символы истинности true (истина) и false (ложь).
B.1.4.2 Константы
Константой может быть любое целое положительное число, строка символов или буквенный набор, начинающийся с буквы нижнего регистра. Кроме того, специальный символ [] рассматривается как константа. Символ подчеркивания (_) рассматривается как заглавная буква. Например, 3, part, ‘standard vendor’, [ ], and qty_on_hand константы.
B.1.4.3 Символьные переменные
Символьные переменные указывают на объекты, даже когда не определено, что это за объект. Переменная – это строка любая буквенная строка, начинающаяся с заглавной буквы и возможно символа подчеркивания. Например, PartName, Part_Type, and X2 переменные.
B.1.4.4 Идентификаторы функций
Идентификатор функции обозначает функцию. У каждой функции определённое количество аргументов и целое положительное число обозначает это количество. Можно использовать функции только для целой арифметики, описанные в секции Словарь.
B.1.4.5 Выражение
Выражение состоит из констант, переменных или функций.
B.1.4.6 Предикатные символы
Предикатный символ обозначает связь. У каждого предикатного символа определённое количество аргументов, описанное положительным целым числом. Обычно это символы типа меньше чем, меньше или равно и так далее, также все цифробуквенные символы, начинающиеся с буквы нижнего регистра. Символ подчеркивания (_) рассматривается как заглавная буква.
B.1.4.7 Символ равенства
Символ равенства = записывается в строго определенной форме. Предложение T1 = T2 означает, что T1 и T2 ссылаются на одно отношение.
B.1.4.8 Высказывания
Высказывание предполагает наличие определенной связи между отношениями. Оно может быть либо верным, либо ложным. Высказывание состоит из символа истинности (например, True), или любого другого предикатного символа. Каждый аргумент высказывания – выражение.
B.1.4.9 Предложения
Каждое высказывание – предложение. Более сложные предложения состоят из простых, и строятся с использованием логических связей и кванторов. Нотация логических связей дается ниже в порядке от более тесной к более слабой. F и G – случайные предложения.
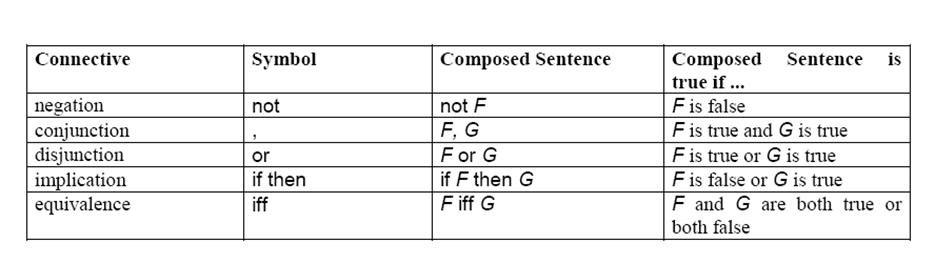
Нотация для кванторов описана ниже. F – случайное предложение.

Неформальная запись
( for all X1, X2, ..., Xn ) ( F )
равносильна
( for all X1 ) ( for all X2 ) ... ( for all Xn ) ( F ).
Переменная, которая не ограничена кванторами, называется свободной.
( for all * ) ( F )
равносильна
( for all X1 ) ( for all X2 ) ... ( for all Xn ) ( F )
где X1, X2, ..., Xn – любые свободные переменные в F.
Квантор существования ( for some ) обозначается по такому же принципу. Закрытым предложением (closed sentence) называется предложение, которое не содержит свободных переменных.
B.1.4.10 Пошаговые описания
Описание предиката позволяет определить его состояние. Обычно это делается закрытым предложением.
( for all X1, X2, ..., Xn ) ( p( X1, X2, ..., Xn ) iff F )
Формально, очень удобно пошаговое описание. Например, логическим выражением if. Так это сделано в закрытом предложении типа
( for all X1, X2, ..., Xn ) ( p( X1, X2, ..., Xn ) ifdef F ).
Это сокращенная форма для предложения
( for all X1, X2, ..., Xn ) ( if F then p( X1, X2, ..., Xn ) )
но это только часть описания. Отметим, что каждый шаг (ifdef ) описания даёт лишь достаточное состояние часть с if. Поэтому, нельзя указывать другой предикат в качестве шага. Правило
p( k1, k2, ..., kn )
где каждый ki константа, рассматривается как
( for all X1, X2, ..., Xn ) ( p( X1, X2, ..., Xn ) ifdef
X1 = k1, X2 = k2, ..., Xn = kn )
Совокупность переменных и констант рассматривается похожим образом. Описание заканчивается установкой необходимого состояния, используя if для усложнения.
Положим
( for all X1, X2, ..., Xn ) ( p( X1, X2, ..., Xn ) ifdef F1 )
( for all X1, X2, ..., Xn ) ( p( X1, X2, ..., Xn ) ifdef F2 )
...
( for all X1, X2, ..., Xn ) ( p( X1, X2, ..., Xn ) ifdef Fm )
это закрытые предложения, описывающие все возможные состояния для p. Все переменные могут быть переименованы в нужный вид. Сложное утверждение для p будет иметь вид
( for all X1, X2, ..., Xn )
( if p( X1, X2, ..., Xn ) then F1 or F2 or ... or Fm ).
Пошаговое описание позволяет показать, что нам известно о предикате в конкретный момент. Сложное утверждение показывает, что всё остальное – ложь. Пошаговое описание не даёт больше возможностей для работы; они просто удобны и кратки. Сочетание пошагового описания и сложных утверждений – эквивалент обычного описания
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.