Оптические свойства твердых тел, страница 2

2.4.2. Оптические спектры твердых тел

В наши дни количественное знание электронной структуры атомов и молекул, а также построенных из них твердых тел базируется на экспериментальных исследованиях оптических спектров отражения, поглощения и пропускания и их квантовомеханической интерпретации. Весьма интенсивно изучается зонная структура и дефектность различных типов твердых тел (полупроводников, металлов, ионных и атомных кристаллов, аморфных материалов). Сопоставление полученных в ходе этих исследований данных с теоретическими расчетами позволило надежно определить для целого ряда веществ особенности строения энергетических зон и величины межзонных промежутков (ширины запрещенной зоны Е_g) в окрестностях главных точек и направлений первой зоны Бриллюэна. Эти результаты позволяют, в свою очередь, надежно интерпретировать такие макроскопические свойства твердых тел, как электропроводность и ее температурная зависимость, показатель преломления и его дисперсия, цвет кристаллов, стекол, керамики, ситаллов и его вариация при радиационном и тепловом воздействиях.

2.4.2.1. Дисперсия электромагнитных волн, показатель преломления

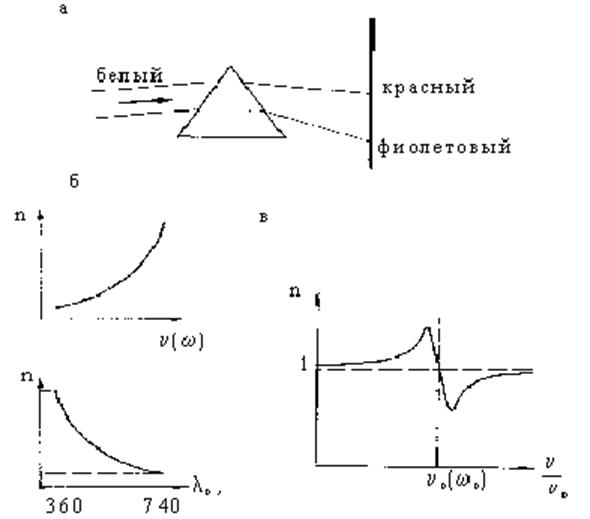
Дисперсия есть явление взаимосвязи показателя преломления вещества, а, следовательно, и фазовой скорости распространения волн, с длиной волны (или частотой) излучения. Так, пропускание видимого света через стеклянную трехгранную призму сопровождается разложением в спектр, причем фиолетовая коротковолновая часть излучения отклоняется наиболее сильно (рис.2.4.2).

          Дисперсия называется нормальной, если с ростом частоты n(w) показатель преломления  n  также возрастает dn/dn>0 (или dn/dl<0). Такой характер зависимости  n от n  наблюдается в тех областях спектра, где среда прозрачна для излучения. Например, силикатное стекло прозрачно для видимого света и обладает в этом интервале частот нормальной дисперсией.

Дисперсия называется аномальной, если с ростом частоты излучения показатель преломления среды уменьшается (dn/dn<0  или dn/dl>0). Аномальная дисперсия соответствует частотам, отвечающим полосам оптического поглощения, физическое содержание явления поглощения будет кратко рассмотрено ниже. Например, для натрийсиликатного стекла полосы поглощения соответствуют ультрафиолетовой и инфракрасной областям спектра, кварцевое стекло в ультрафиолетовой и видимой части спектра обладает нормальной дисперсией, а в инфракрасной - аномальной.

Рис. 2.4.2. Дисперсия света в стекле: а – разложение света стеклянной призмой, б – графики n = n(n) и n = n(l₀) для нормальной дисперсии, в – при наличии нормальной и аномальной дисперсии В видимой и инфракрасной части спектра нормальная дисперсия характерна для многих щелочно-галоидных кристаллов, что и обусловливает широкое их использование в оптических приборах для инфракрасной части спектра.

Физическая природа нормальной и аномальной дисперсии электромагнитных волн становится понятной, если рассмотреть это явление с позиций классической электронной теории. Рассмотрим простой случай нормального падения плоской электромагнитной волны оптического диапазона на плоскую границу однородного диэлектрика. Связанные с атомами электроны вещества под действием переменного поля волны напряженностью          совершают вынужденные колебания с той же круговой частотой w, но с фазой j, отличающейся от фазы волн. С учетом возможного затухания волны в среде с собственной частотой колебании электронов w₀, уравнение вынужденных поперечных колебаний в направлении  - направлению распространения плоскополяризованной волны - имеет вид

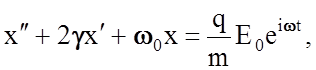                                                (2.4.13)

известный из курса общей физики  (q и m - заряд и масса электрона).

Для оптической области w₀» 10¹⁵ с^-1, а коэффициент затухания g может быть определен в идеальной среде при условии нерелятивистской скорости движения электрона (u<<c) из соотношения

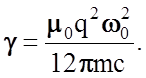                                                                        (2.4.14)

При  w₀ = 10¹⁵ с^-1 величина g » 10⁷  с^-1. Пренебрегая сравнительно непродолжительной стадией неустановившихся колебаний, рассмотрим частное решение неоднородного уравнения (2.4.13) на стадии установившихся колебаний. Решение ищем в форме

                                                                           (2.4.15)

Тогда из уравнения (2.4.13) получим

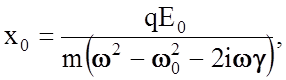
или , где амплитуда колебаний равна

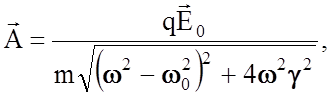                                             (2.4.16)

здесь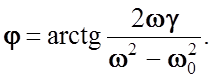    

Тогда решение для координаты (2.4.15) можно переписать в виде

                                                                     (2.4.17)

Таким образом, вынужденные гармонические колебания электрона происходят с амплитудой A  и опережают по фазе колебания в падающей волне на угол j. Вблизи резонансного значения  w = w₀ зависимость  A  и j  от w/w₀ представляет особый интерес.

На рис. 2.4.3 представлены графики зависимостей амплитуды и фазы вблизи резонансной частоты.

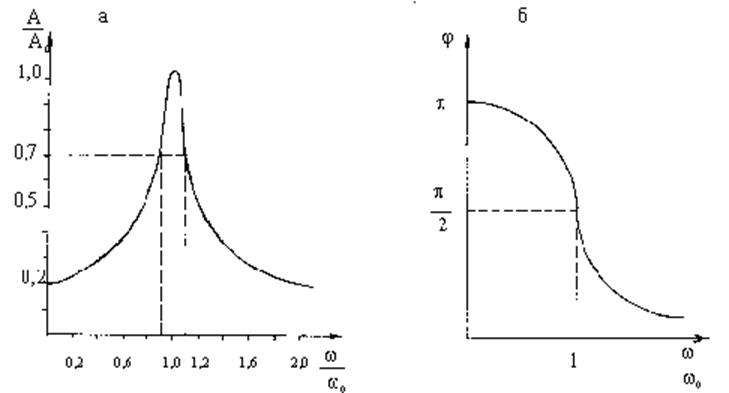Рис. 2.4.3. Графики амплитуды (а) и фазы (б) колебаний электронов вблизи резонансной частоты (при g » 0,1w₀)

В реальных случаях обычно g меньше, чем g » 0,1 w₀, выбранная для наглядности на рис.2.4.3, амплитуда и фаза меняются более резко. Если падающий на диэлектрик свет не является монохроматическим, то вблизи резонанса, на частотах w®w₀, он поглощается, электроны вещества рассеивают эту энергию в объеме. Так возникают в спектрах полосы поглощения. Ширина линий спектра поглощения определяется формулой