Методы определения механических свойств твердых тел и основные результаты

3.9. МЕТОДЫ ОПРЕДЕЛЕНИЯ МЕХАНИЧЕСКИХ СВОЙСТВ  ТВЕРДЫХ ТЕЛ И ОСНОВНЫЕ РЕЗУЛЬТАТЫ

3.9.1. Упругие константы материалов

Важнейшими физическими параметрами, определяющими макро- и микроскопические механические свойства твердых тел, являются модули упругости Е  и G. Различают статические и динамические методы определения величин модулей. Статические методы (растяжение), и некоторые динамические (кручение, изгибные колебания) требуют значительных деформаций и более применимы к металлам. При исследованиях хрупких и малопластичных материалов широко используется динамический импульсный метод. Измеряются скорости прохождения через образец импульсных волн, длина которых мала по сравнению с длиной образца, т.е. волны ультразвукового диапазона с частотами порядка мегагерц.

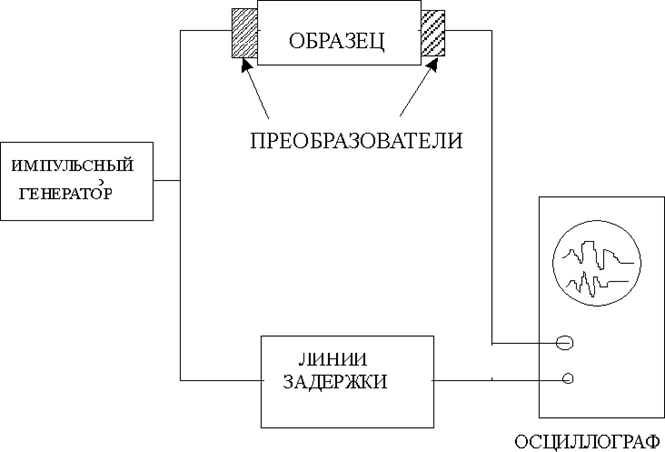Рис.3.9.1.Принципиальная схема динамического импульсного ультразвукового метода измерения упругих констант твердого тела

Измерительный комплекс обычно прост и включает импульсный генератор с преобразователями, в которых электромагнитные колебания преобразуют в механические волны продольного или поперечного (сдвигового) типа, подаваемые в образец, одно- или двухлучевой осциллограф, регистрирующий входящий и прошедший (или отраженный) сигналы от преобразователя, где осуществлен обратный процесс преобразования "механическая волна ® электрический сигнал" (рис.3.9.1).

Чаще всего используют пьезоэлектрические преобразователи механического импульса в электрический и наоборот. Удобным дополнением схемы является переменная линия задержки, применяемая для точного измерения времени прохождения импульса через образец.

Экспериментально определенные скорости упругих волн связаны с модулями упругости. Для продольной волны

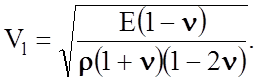                                                          (3.9.1)

Для поперечной (сдвиговой) волны

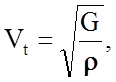                                                                              (3.9.2)

где r - плотность материала, кг/м³; n - коэффициент Пуассона, зависящий от вида напряженного состояния.

Ультразвуковой импульсный метод позволяет определять модули как в различных направлениях монокристаллических образцов, соответствующим образом вырезанных из монолита, так и поликристаллических и аморфных материалов, ультразвуковые методы позволяют по затуханию амплитуды сигнала исследовать также наличие и подвижность дефектов микроструктуры, даже оценивать пористость материала. Исследована широкая гамма веществ различных классов - окислов, галоидных соединений, карбидов, металлов. Некоторые из полученных О.Андерсеном данных приведены в табл.3.9.1 (пористость не оговорена). Там же приведена расчетная температура Дебая q_Д, речь о которой шла в Части 2.

Температура Дебая q_Д является важным параметром твердого тела. Она входит в уравнение, описывающее свойства, которые связаны с колебанием атомов решетки, и в фононные теории. Ультразвуковой метод измерения продольной V_l  и поперечной V_t  скоростей позволяет определить q_Д для веществ по формуле

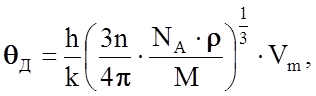                                                  (3.9.3)

                 Таблица3.9.1

Скорости упругих волн и упругие изотропные константы некоторых веществ (средние округленные значения)

Вещество	Модуль Юнга Е, ГПа	Модуль сдвига G, ГПа	Коэффициент Пуассона n	Скорость продольной волны,Vl, м/с	Скорость поперечной волны, Vt,м/с	Температура Дебая qД, К
Алмаз	1141	533	0,07	18120	12323	2240
Al	77,4	28,6	0,353	6794	3235	426,6
BaTiO3	163	61	0,346	6835	3317	450
CaF2	111	43	0,297	6813	3659	508
Cu	137,4	51,4	0,339	4833	2388	344,5
Fe	223	87	0,285	6064	3325	479
Fe3O4	231	91	0,262	7382	4192	642
Fe2O3	212	93	0,139	6582	4260	694
KCl	25	10	0,272	3972	2224	228
LiF	124	51	0,205	7233	4405	717
MgO	286	122	0,178	9361	5859	901
Si	163	67	0,223	8945	5341	638
Лёд	9,3	3,6	0,304	3633	1929	203
a-кварц	49,5	44	0,076	6040	4053	586
b-кварц	103	43	0,199	6720	4102	560
Плавленый кварц	73	31	0,172	5750	3767	495

где h, k - постоянные Планка и Больцмана соответственно, n - число атомов в молекуле,  N_А- число Авогадро, r - плотность вещества, М - его молекулярная масса, V_m - так называемая средняя скорость звука в веществе. Для изотропных веществ соотношение между V_m и продольной V_l и поперечной V_t скоростями звука имеет вид

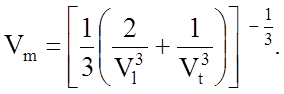                                                      (3.9.4)

Все соотношения: (3.9.1), (3.9.2), (3.9.3), (3.9.4) - справедливы для полностью изотропных тел, таких, как ненапряженное стекло и поликристаллические материалы, в которых величины V_l и V_t не зависят от направлений в образце. Наличие текстуры, значительная пористость и неоднородность структуры могут внести заметные искажения. На этом эффекте, в частности, основана методика оценки пористости материалов. Например, Ганом  после испытаний серии специально изготовленных образцов с заданной пористостью, получены соотношения для пористости в окиси алюминия:

Е = 4050 - 128 р, кбар

G = 1650 - 55 р, кбар,

где р - пористость, и для окиси магния

Е = 3050(1 - 5,21р  + 5,10p², кбар,

G = 1290(1 - 3,82р + 3,16 p², к6ap,

(1 кбар = 10⁸ Па).

Группой исследователей (Л.Б.Зуев, В.Е.Громов и др.) предложена методика определения  и увеличения ресурса работы стальных изделий на основе прецизионного измерения скорости звука в изделии и отслеживании динамики ее изменения по мере накопления повреждений структуры.

Поскольку величины упругих модулей определяются характером и величиной межатомных сил, то на их величину влияют многие факторы:

·  тип решетки (см. данные в табл.3.9.1 для различных модификаций SiO₂);

·  валентность атомов (см. данные для Fe₂O₃ и Fe₃O₄ там же);