Изменяя основные параметры системы атомов (температуру, давление) любое вещество можно перевести в конденсированное твердое состояние или из жидкого состояния, или непосредственно из паровой фазы. На рис. 1.3.9 представлена фазовая диаграмма для однокомпонентной системы - H2O. При низких температурах и повышенных давлениях все вещества можно перевести в твердое состояние, иногда с весьма непривычными свойствами. Например, при давлении, большем 21700 атмосфер, вода существует в виде льда VII, плотность которого близка к 1,5 г/см3, а температура плавления при 32000 атмосфер составляет + 192oC. Очень горячий лед!
Возникновение той или иной кристаллической структуры с параметром а0 является процессом, энергетически выгодным для данных условий воздействия на тело окружающей среды. В соответствии с законами термодинамики все атомы, ионы или молекулы кристалла стремятся занять пространственные положения, соответствующие минимуму свободной энергии системы.
При термодинамическом описании процессов плавления, конденсации, полиморфизма, то есть превращения фаз, применяются основные функции термодинамики: энтальпия, энтропия, теплоемкость, свободная энергия.
Термодинамическая функция, называемая энтальпией Н (или теплосодержанием), характеризует запас энергии, приобретенный системой или материалом, и возрастает с увеличением температуры:
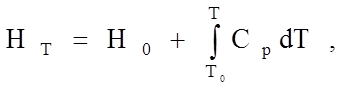(1.7.1)
где H0 и HT - энтальпия при начальной и данной температурах, Сp -теплоемкость при постоянном давлении. Численное значение энтальпии можно найти двумя способами. Если U - величина внутренней энергии, pV- работа, совершенная над телом окружающей средой, то можно записать
H = U + pV, (1.7.2)
где р и V - давление и объем материала.
Второй способ предполагает использование представления о свободной энергии Гельмгольца (F) или Гиббса (G) материала, а также произведения Т×S (абсолютной температуры на энтропию), характеризующего степень внутреннего беспорядка тела:
H = F + TS + pV = G + TS. (1.7.3)
Отметим, что величину F = U - TS называют свободной энергией Гельмгольца или изохорно-изотермным потенциалом. Эта функция будет минимальна для равновесного, устойчивого состояния системы. Но поскольку твердые тела могут быть весьма сложной формы и постоянство их мало изменяющегося объема контролировать часто неудобно, предпочтительнее использование изобарно-изотермного потенциала G = F + pV, называемого иначе свободной энергией Гиббса. В таком случае минимум свободной энергии G характеризует устойчивое равновесное состояние системы при данных температуре Т и давлении p. Представим условным графиком (рис.1.7.1) характер изменения основных термодинамических функций H, S, G с ростом температуры Т.
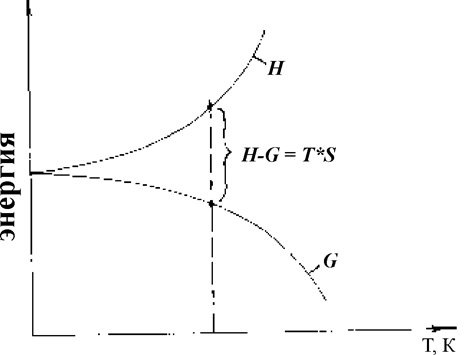Рис.1.7.1. Связь основных термодинамических функций с
ростом температуры
Очевидно, что при Т = 0К величина Н =G; с ростом температуры энтальпия H увеличивается, а свободная энергия G уменьшается, так как непрерывно увеличивается с температурой энтропия S, характеризующая степень неупорядоченности структуры.
Между скоростью изменения свободной энергии и энтропией существует связь. Продифференцируем уравнение (1.7.3) по температуре:
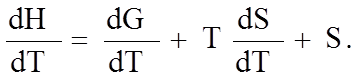(1.7.4)
В уравнение (1.7.4) необходимо подставить известные из термодинамики соотношения
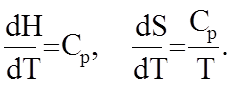(1.7.5)
Тогда получим
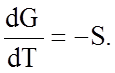(1.7.6)
При этом необходимо помнить, что энтропия S - всегда положительна и увеличивается с ростом температуры, а поэтому наклон кривой, описывающей G = G (Т), непрерывно увеличивается.
В данном случае важно, что с понижением температуры уменьшается энтропия и возрастает степень упорядоченности структуры. Свободная энергия при переходе системы в более устойчивое состояние уменьшается. Например, в известной реакции при 273К
H2O лед Û H2O вода
для смещения вправо требуется повышение температуры. Во многих справочниках энергия превращения описывается изменением энтальпии. Поясним на рис. 1.7.2, что это обозначает на примере воды.
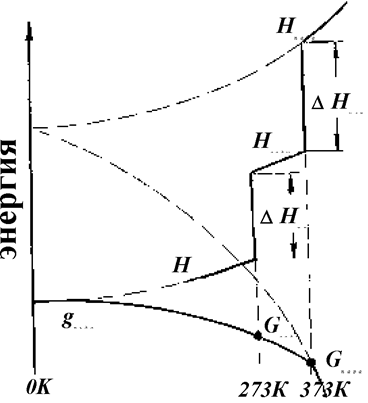
Рис. 1.7.2. Энергия превращений воды и изменения функций Н и G, описывающих ее состояние
Испарение и расплавление воды требует подвода извне энергии, величина которой зависит также и от давления. Поскольку и плавление, и испарение уменьшают координацию атомов и молекул, то происходит возрастание неупорядоченности и энтропии системы.
Выполняются соотношения
DНпл = Тпл×DSпл, (1.7.7)
DНисп = Тисп×DSисп. (1.7.8)
В точках превращений свободная энергия для обеих фаз остается одинаковой, но функция G = H - TS испытывает перегиб.
Способность материала образовывать несколько кристаллических структур (модификаций) одинакового в среднем химического состава называется п о л и м о р ф и з м о м. Различные модификации одного и того же вещества называют а л л о т р о п и ч е с к и м и м о д и ф и к а ц и я м и.
Полиморфизм широко распространен в различных технических материалах и играет крайне важную роль при их обработке и эксплуатации изделий. Он характерен как для чистых элементов - углерода, фосфора, олова, железа, кремния и других, так и, в особенности, для многоатомных соединений.
Бюргером предложена классификация структурных полиморфных изменений, особенно полезная при анализе кинетики превращений. Выделено четыре основных группы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.