Информатика и выч. техника \ Теория и обработка сигналов

Цифровые фильтры с конечной импульсной характеристикой. Вариант 8, страница 3

stem(k1)

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Окно Кайзера, beta = 0')

[K1,w]=DTFT(k1,512);

subplot(212)

plot(w,abs(K1))

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Амплитудный спектр')

k2=kaiser(N,1);

figure(2)

subplot(211)

stem(k2)

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Окно Кайзера, beta = 1')

[K2,w]=DTFT(k2,512);

subplot(212)

plot(w,abs(K2))

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Амплитудный спектр')

k3=kaiser(N,5);

figure(3)

subplot(211)

stem(k3)

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Окно Кайзера, beta = 5')

[K3,w]=DTFT(k3,512);

subplot(212)

plot(w,abs(K3))

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Амплитудный спектр')

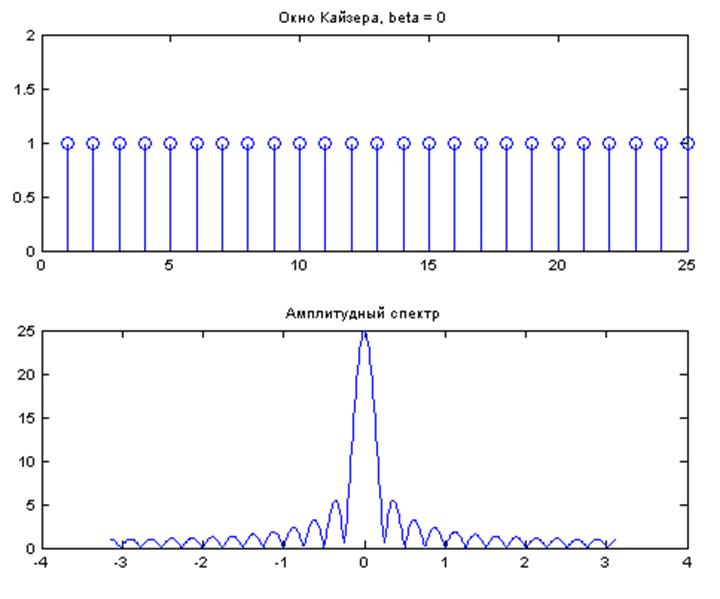
Рис. 8. Графики: окно Кайзера для  β = 0  и его амплитудный спектр.

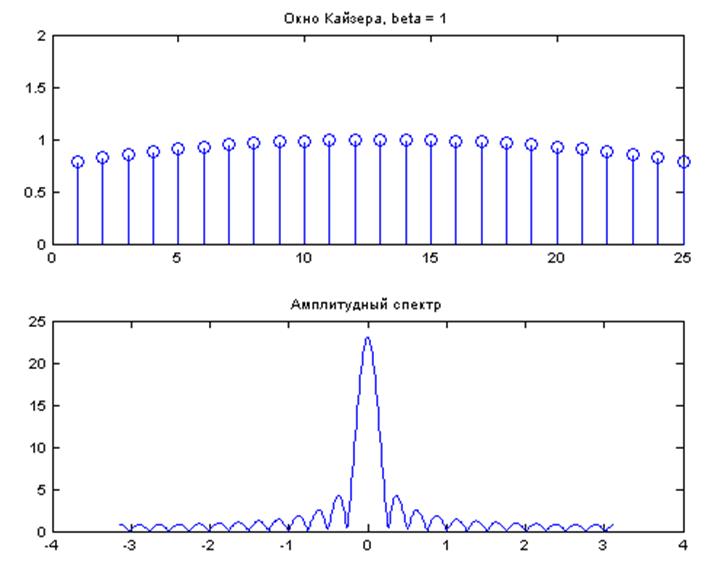
Рис. 9. Графики: окно Кайзера для  β = 1  и его амплитудный спектр.

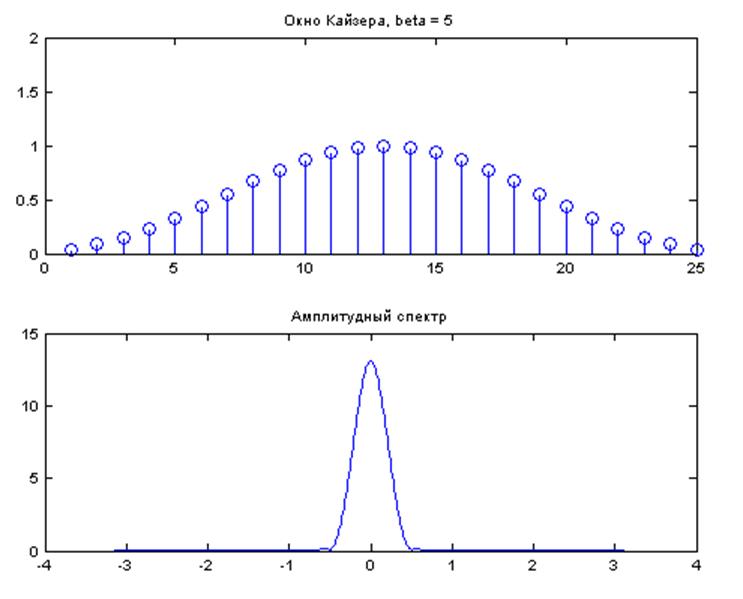
Рис. 10. Графики: окно Кайзера для  β = 5  и его амплитудный спектр.

Для прямоугольного окна и окон: Хэмминга, Ханна и Блэкмана  единственным управляемым параметром является размер окна. Но относительные уровни боковых лепестков и, значит, пульсации (отклонения) в полосах пропускания и задерживания  у таких окон не зависят от  длины окна.

Более гибкие возможности предоставляет так называемое окно Кайзера.  Функция, описывающая его поведение

               

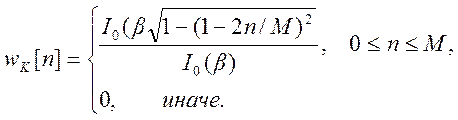
Здесь   - модифицированная функция Бесселя первого рода нулевого порядка,

          М  - порядок фильтра, позволяющий управлять шириной переходной области фильтра,

           - параметр формы окна, с помощью которого можно регулировать амплитуду боковых лепестков и форму окна.

При увеличении  относительный уровень боковых лепестков уменьшается, и график амплитудного спектра становится более гладким. Но увеличивается ширина главного лепестка, и, следовательно, увеличивается ширина переходной полосы.

Для построения окна Кайзера в Matlab используется функция  kaiser(N, beta).

8. Расчет фильтра. Построение графика АЧХ спроектированного фильтра.

График спецификации   фильтра

             

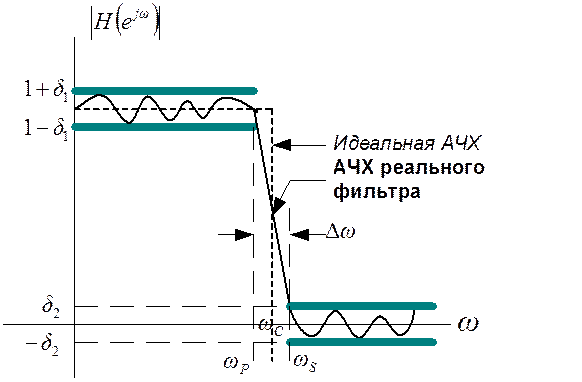
               - граничная частота полосы пропускания,

               - граничная частота полосы задерживания,   

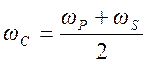 - частота  среза  фильтра,

 - допустимый уровень отклонений (пульсаций) АЧХ в полосе пропускания,

- допустимый уровень отклонений (пульсаций) АЧХ в полосе задерживания.

Исходные требования к фильтру:

·  ,

·  ,

·   рад/с,

·   рад/с.

Проектирование фильтра:

1.  Частота среза фильтра 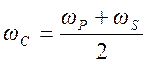 ,  Нормированная угловая переходная полоса  .

 2. Определение допустимого уровень пульсаций   как  или в децибелах  . Такому уровню ошибки аппроксимации идеальной АЧХ  фильтра соответствует окно Блэкмана, для которого  A = 74 дБ. 

3. Определение порядка фильтра с окном Блэкмана по выражению:

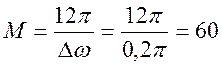
  4. Окно Блэкмана фильтра:

            

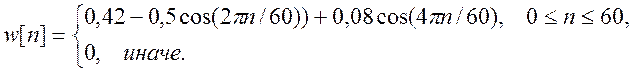
5. Импульсная характеристика рассчитанного фильтра:

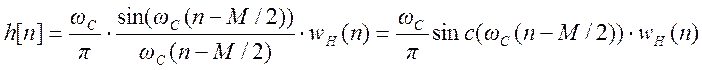
M=60;

n=0.001:M;

wc=0.65*pi;

w=0.42-0.5*cos(2*pi*n./M)+0.08*cos(4*pi*n./M);

h=w.*((wc*sin(wc.*(n-(M/2))))./(pi*wc*(n-(M/2))));

[H,w]=DTFT(h,512);

figure(1)

plot(w,abs(H)), grid

xlabel('rad/s')

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 10);

title ('Амплитудно-частотная характеристика фильтра')

figure(2)

plot(w,20*log10(abs(H)))

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 10);

title ('Логарифмическая АЧХ фильтра')

grid

xlabel('rad/s')

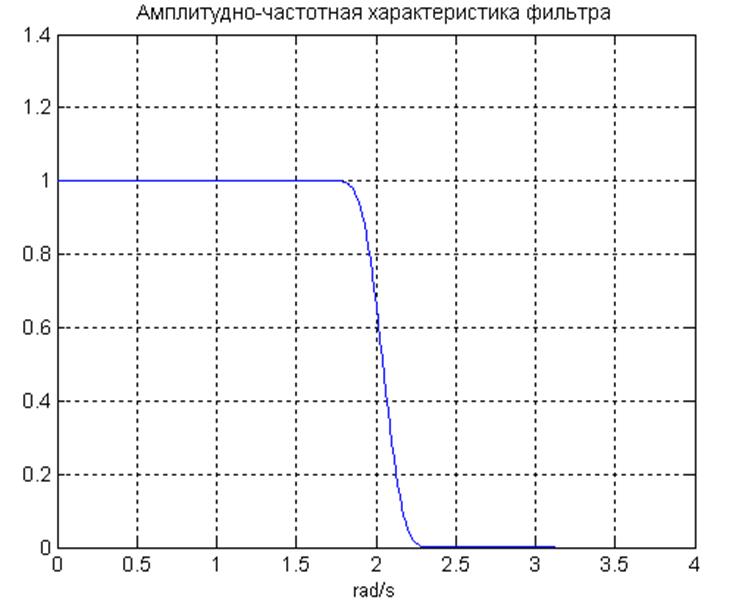
Рис.11. Амплитудно-частотная характеристика спроектированного фильтра.

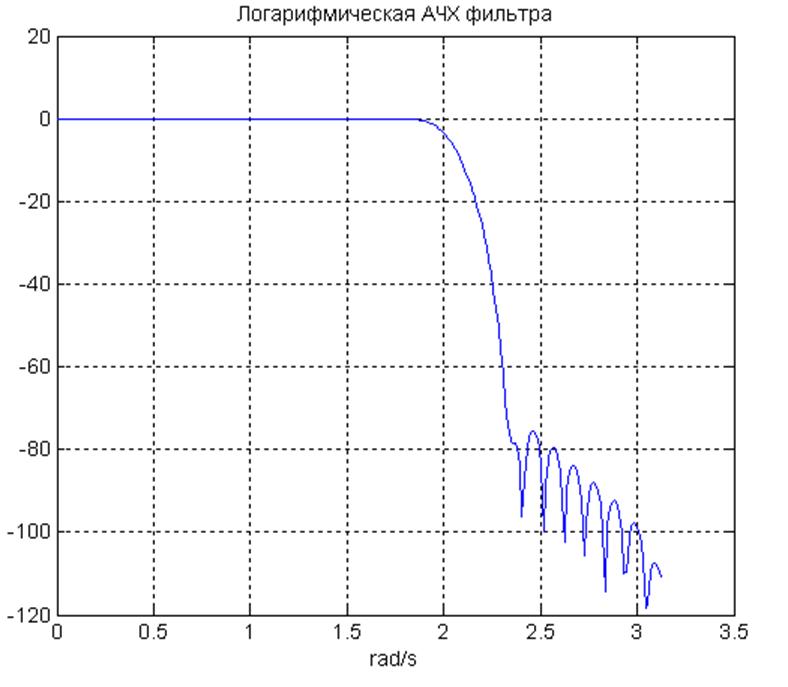
Рис. 12. Логарифмическая амплитудно-частотная характеристика спроектированного фильтра.

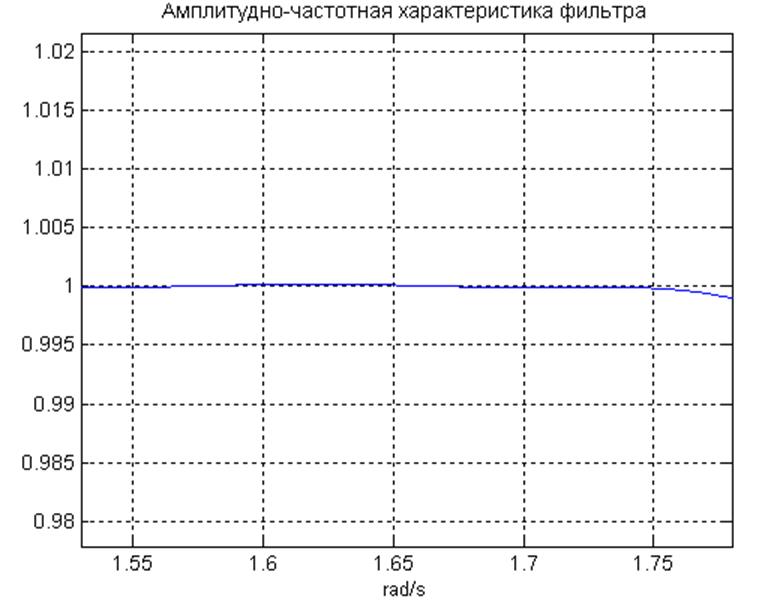
Рис.13.  Пульсации в полосе пропускания.

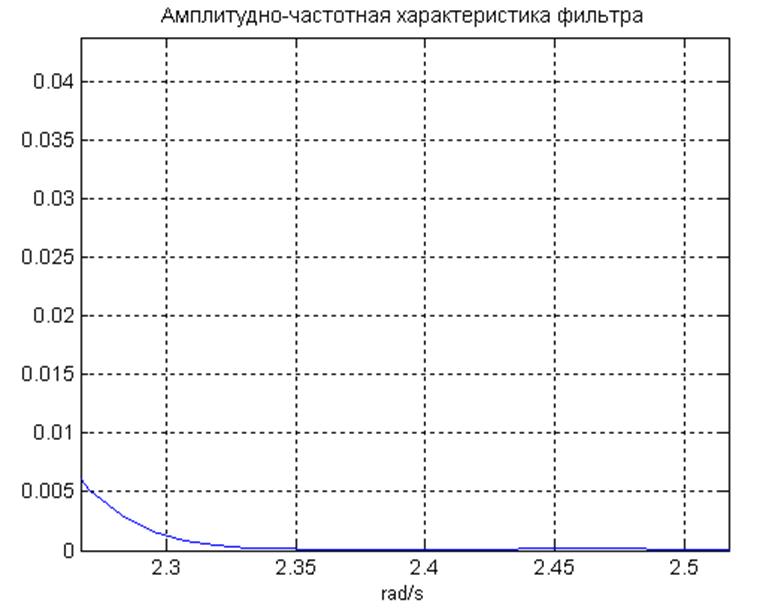
Рис.14. Пульсации в полосе задерживания.

Из графиков можем сделать вывод, что спроектированный фильтр соответствует исходным требованиям. Полоса пропускания фильтра от 0 до 1.72 рад/с (по требованиям до ), полоса задерживания начинается с 2.4 рад/с (по требованиям с ). Пульсации в полосе пропускания и в полосе задерживания не превышают 0.0005.

9.  Фильтрация сигнала speech при помощи спроектированного фильтра и оценка качества звучания сигнала до и после фильтрации.

Matlab Script (labwork10_8)

load('speech.mat');

M=61;

n=0:M-1;

wc=0.65*pi;

w=0.42-0.5*cos(2*pi*n./M)+0.08*cos(4*pi*n./M);

wc = 0.5*pi;

h = w.*(wc*sin(wc.*(n-(M/2))))./(pi*wc*(n-(M/2)));

y = conv(nspeech2,h);

[Y,w] = DTFT(nspeech2,512);

subplot(2,1,1);

plot(w./(2*pi),abs(Y));

title ('Амплитудный спектр исходного сигнала');

xlabel('f, Гц');grid;

[Y1,w] = DTFT(y,512);

subplot(2,1,2);

plot(w./(2*pi),abs(Y1));

title ('Амплитудный спектр сигнала после фильтрации спроектированным фильтром');

xlabel('f, Гц');grid;

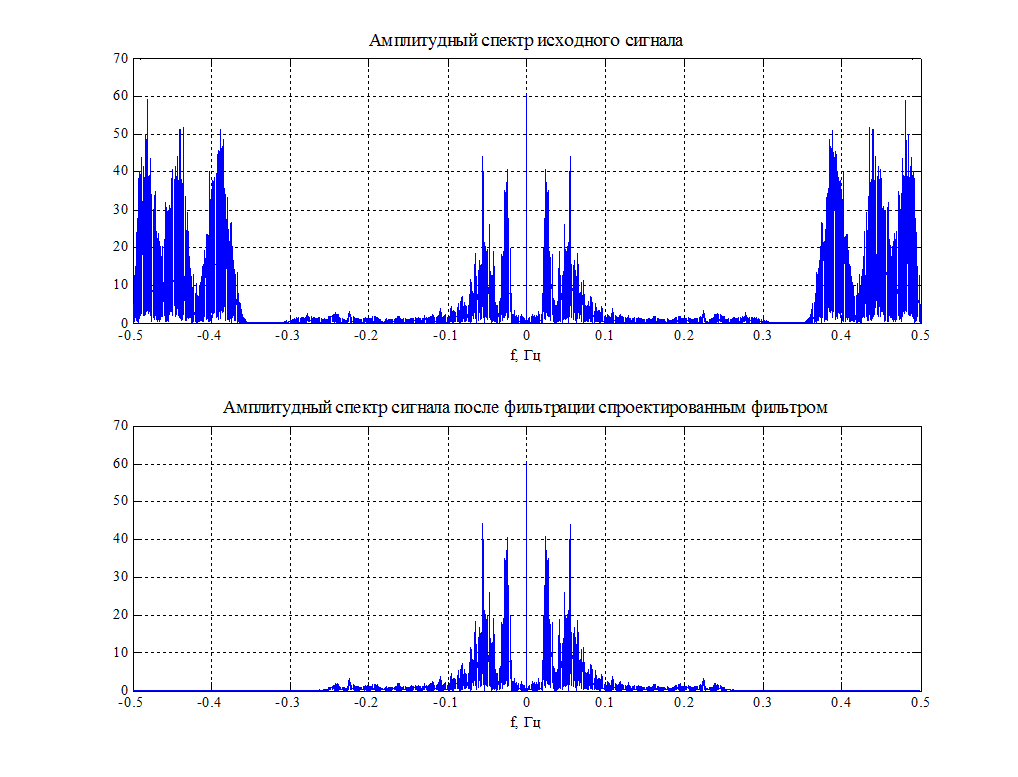
Рис.15.  График свертки исходного сигнала и импульсной характеристики спроектированного фильтра.

Комментарии:

При прослушивании отфильтрованного сигнала, наблюдается хорошее подавление шумов, но и уровень полезного сигнала стал ниже.


Выводы:

  • Синтез КИХ фильтров осуществляется несколькими способами:
    • методом разложения частотной характеристики в ряд Фурье;
    • методом взвешивающих окон;
    • методом частотных выборок;
    • методом наименьших квадратов;

·  При выполнение данной лабораторной работы был разработан КИХ-фильтр методом взвешивающих окон. Этот метод заключается в переходе от идеального фильтра к его ИХ при помощи преобразования Фурье, усечения этой характеристики и улучшения ее при помощи той или иной оконной функции (окно Хэмминга,окно Ханна, окно Блэкмана, окно Кайзера и др.), удовлетворяющей требованиям полосы пропускания и задерживания разрабатываемого КИХ-фильтра, определения порядка фильтра с учетом выбранной оконной функции и нахождения коэффициентов ИХ фильтра.

Скачать файл