Цифровые фильтры с конечной импульсной характеристикой. Вариант 8, страница 2

>> y2 = conv(nspeech2,h2);    %свертка исходного сигнала с ИХ фильтра (N = 50)

>> sound(nspeech2)            %прослушивание исходного сигнала

>> sound(y1)            %прослушивание отфильтрованного сигнала фильтром (N = 15)

>> sound(y2)            %прослушивание отфильтрованного сигнала фильтром (N = 50)

Matlab Script (labwork10_3.m)

load('speech.mat');

N1 = 16;

N2 = 50;

n1 = 0:N1-1;

n2 = 0:N2-1;

wc = 2;

h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));% ИХ с длиной фильтра 15

h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));% ИХ с длиной фильтра 50

y1 = conv(nspeech2,h1);%свертка исходного сигнала и ИХ первого фильтра

y2 = conv(nspeech2,h2);%свертка исходного сигнала и ИХ второго фильтра

%постоение графиков амплитудного спектра

%Амплитудный спектр исходного сигнала

[Y,w] = DTFT(nspeech2,512);

subplot(3,1,1);

plot(w./(2*pi),abs(Y));

title ('Амплитудный спектр исходного сигнала');

xlabel('f, Гц');grid;

%Амплитудный спектр сигнала после фильтрации (N = 15)

[Y1,w] = DTFT(y1,512);

subplot(3,1,2);

plot(w./(2*pi),abs(Y1));

title ('Амплитудный спектр сигнала после фильтрации (N = 15)');

xlabel('f, Гц');grid;

%Амплитудный спектр сигнала после фильтрации (N = 50)

[Y2,w] = DTFT(y2,512);

subplot(3,1,3);

plot(w./(2*pi),abs(Y2));

title ('Амплитудный спектр сигнала после фильтрации (N = 50)');

xlabel('f, Гц');grid;

 

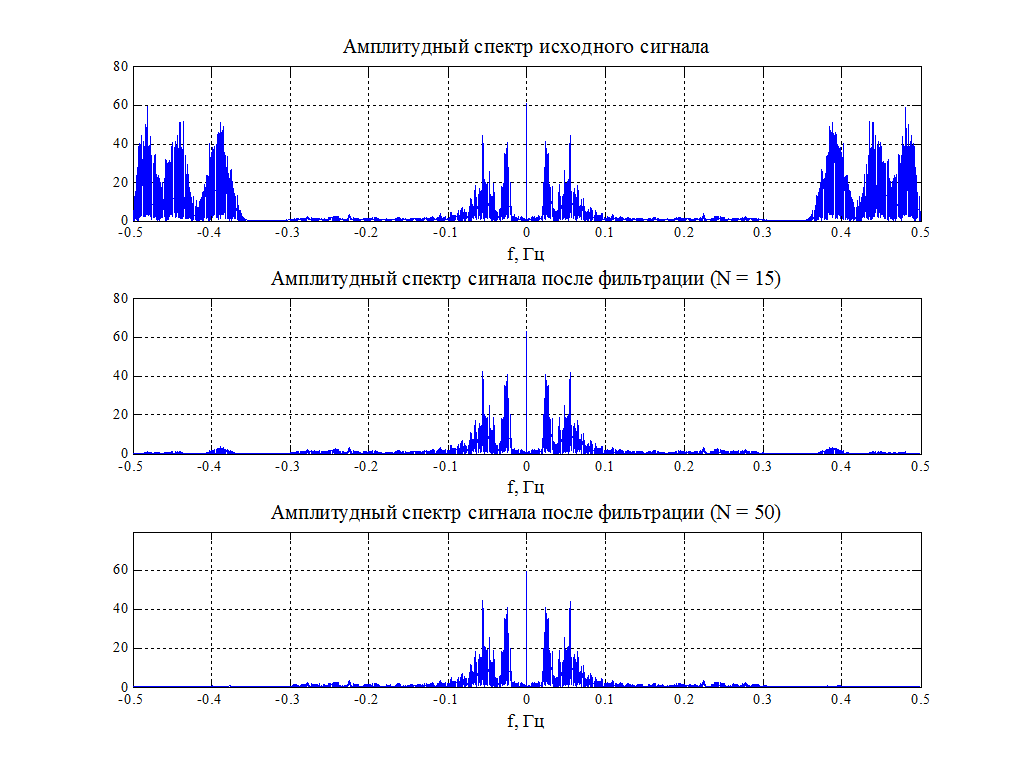
Рис. 5.  Графики амплитудных спектров исходного сигнала и отфильтрованного сигнала  КИХ-фильтром

нижних частот с прямоугольным окном частотой среза  с длиной фильтра  N = 15 и N = 50 .

Комментарии:

Исходный сигнал (nspeech2) представляет собой смесь полезного сигнала (речь) с шумом (шипение на фоне речи). Как видно из графика амплитудных спектров (Рис. 5), исходный сигнал состоит из низкочастотной высокочастотной составляющих.

При прохождении исходного сигнала через фильтр, длина которого 15, высокочастотная составляющая практически полностью подавляется и шумы при прослушивании уменьшаются.

При прохождении исходного сигнала через фильтр, длина которого 50, высокочастотная составляющая подавляется еще лучше и шумы практически полностью исчезают.

4.  Построение графиков прямоугольного окна и окон Хэмминга, Ханна, Блэкмана для N = 25.

Matlab Script (labwork10_4.m)

N = 25;

n = 0:N-1;

h1 = rectpuls(n-12,N-2);

h2 = hamming(N);

h3 = hann(N);

h4 = blackman(N);

plot(n,h1,n,h2,n,h3,n,h4);

legend('Прямугольное окно','Окно Хэмминга','Окно Ханна','Окно Блэкмана');

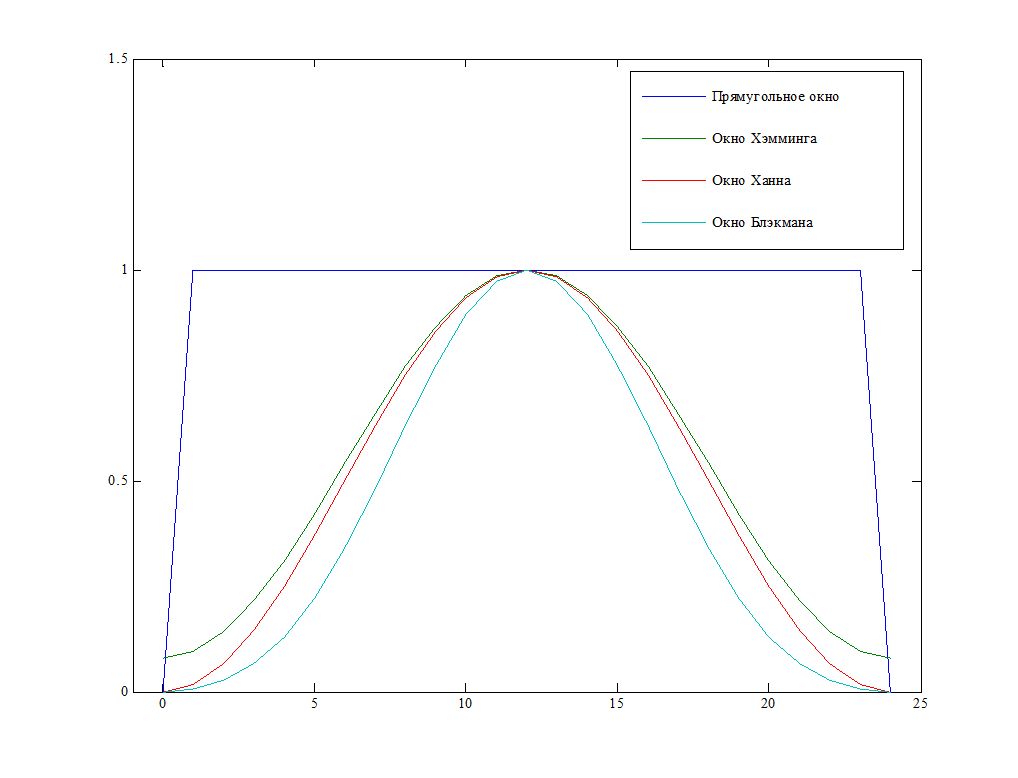
Рис. 6. Графики прямоугольного окна, окна Хэмминга, окна Ханна и окна Блэкмана для N = 25.

Комментарии:

Для формирования оконных функции в Matlab имеются специальные функции:

hamming (N) - возвращает - значений симметричного окна Хэмминга.

hann (N) - возвращает - значений симметричного окна Ханна.

blackman (N) - возвращает - значений симметричного окна Блэкмана.

Сглаживающие окна применяются для улучшения характеристик фильтра.

5. Вычисление ДВПФ оконных функций из предыдущего пункта и построение графиков амплитудных спектров в шкале децибел.

[H,w]=DTFT(h(n),512);

[X,w]=DTFT(x,512);

[F,w]=DTFT(f,512);

[B,w]=DTFT(b,512);

subplot(411)

plot(w,20*log10(abs(H)))

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Прямоугольное окно')

grid

subplot(412)

plot(w,20*log10(abs(X)))

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Окно Хэмминга')

grid

subplot(413)

plot(w,20*log10(abs(F)))

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Окно Ханна')

grid

subplot(414)

plot(w,20*log10(abs(B)))

set (gca, 'FontName', 'Time New Roman Cyr', 'FontSize', 8);

title ('Окно Блэкмана')

grid

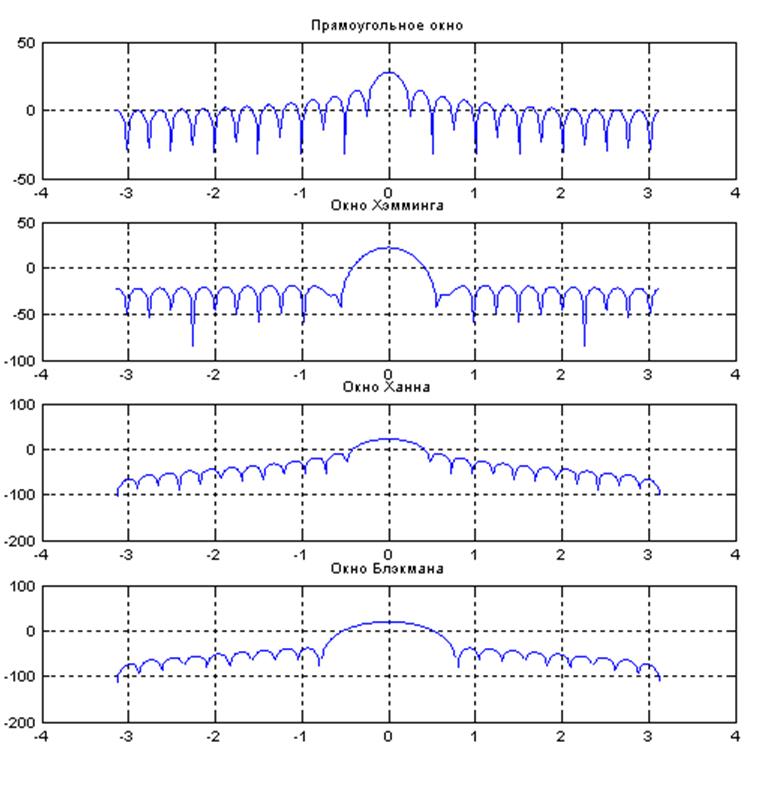
Рис. 7. Графики амплитудных спектров в шкале децибел прямоугольного окна, окна Хэмминга, окна Ханна, окна Блэкмана.

Общие требования к функциям окон заключаются в том, что окно тем лучше сглаживает, чем меньше у него ширина главного лепестка и чем меньше площадь под боковыми лепестками, но эти два условия противоречивы.

Из графиков видно, что прямоугольное окно имеет наименьшую ширину главного лепестка, но максимальный уровень боковых лепестков.

Окно Блэкмана, наоборот, самый низкий уровень боковых лепестков и наиболее широкий главный лепесток.

6. Определение ширины главного лепестка и относительного уровня боковых лепестков в децибелах (относительно амплитуды главного лепестка). Составление таблицы с измеренными и соответствующими теоретическими значениями величин и их разностями.

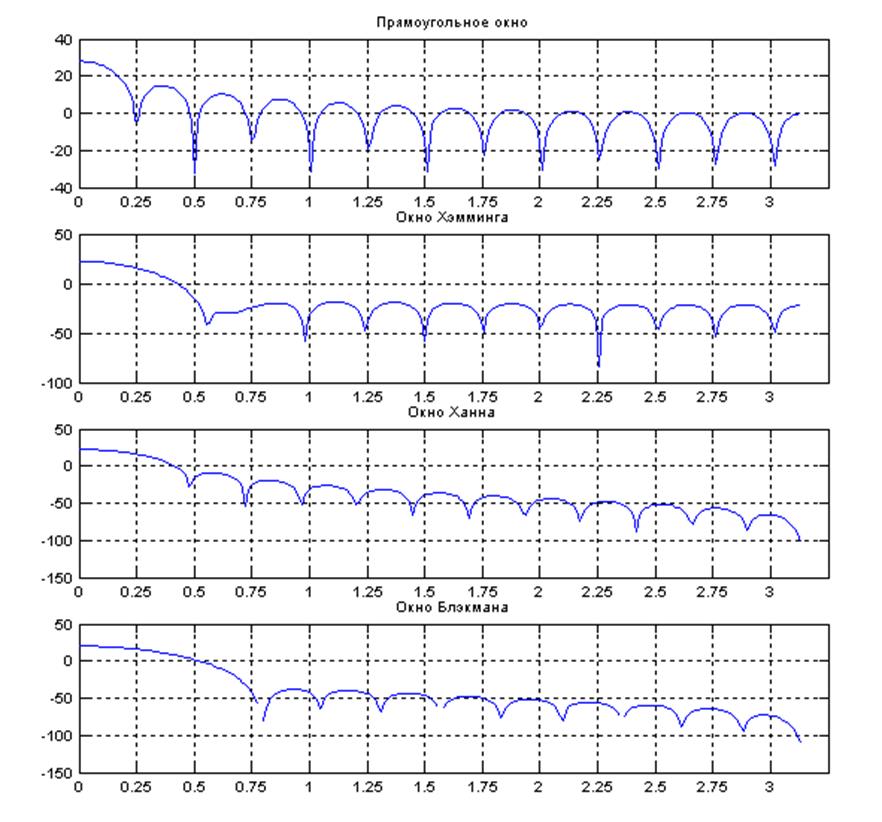
Тип  окна	Ширина  главного  лепестка (теоретическое)	Ширина главного лепестка (измеренное)	Разница
Прямоугольное Ханна Хэмминга Блэкмана	0,5027 1,0053 1,0053 1,5080	0,5000 0,9560 1,1000 1,6000	0,0027 0,0493 0,0947 0,0920

Табл. 2. Теоретические и измеренные значения ширины главного лепестка для окон: прямоугольного, Ханна, Хэмминга,  Блэкмана.

Тип  окна	Относительный  уровень  боковых лепестков, дБ (теоретическое)	Относительный  уровень  боковых лепестков, дБ (измеренное)	Разница
Прямоугольное Ханна Хэмминга Блэкмана	-13 -31 -41 -57	-13.26 -31.49 -42.3 -58.13	0.26 0.49 1.30 1.13

Табл. 3. Теоретические и измеренные значения относительного уровня боковых лепестков для окон: прямоугольного, Ханна, Хэмминга, Блэкмана.

Вывод: теоретические и измеренные значения практически совпадают. Для более точно измерения в Matlab можно использовать функцию zoom().

7. Построение графиков окон Кайзера  и их амплитудных спектров  для       

N = 25, β = 0, β = 1 и β = 5, используя для этого функцию  kaiser(N, beta) и функцию DTFT() с 512 отсчетами частот.

N=25;

k1=kaiser(N,0);

figure(1)

subplot(211)