Спектральные представления периодических сигналов. Вычисление и построение графиков спектров сигналов в среде MATLAB. Вариант 3

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

Дисциплина  «Теория  и  обработка  сигналов»

ЛАБОРАТОРНАЯ  РАБОТА  № 2

СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ

ПЕРИОДИЧЕСКИХ СИГНАЛОВ

Группа:  АТ-53

Студент: Першина Ж. С.

Вариант: 3

Преподаватель:  доц. Щетинин Ю. И.

Новосибирск, 2007

Цель работы:

Изучение понятия спектра  периодического сигнала, приобретение практических навыков вычисления и построения  графиков спектров   сигналов в  среде MATLAB.

1.

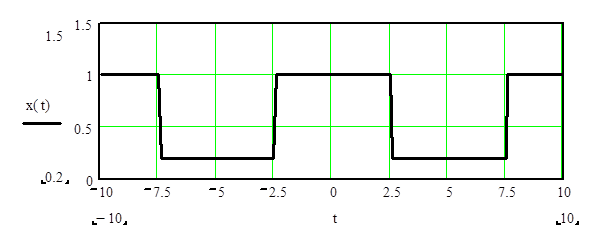
Рис. 1. Спектр периодической последовательности прямоугольных импульсов.

Ряд  Фурье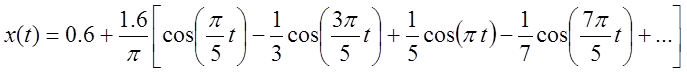  

·  Функция:     ; 

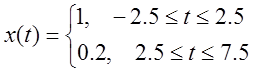·  Амплитуда: А=0.4;

·  Период: T=10;

·  Частота основной гармоники:  ω0=.

1.  Коэффициенты комплексного ряда Фурье (аналитический метод).

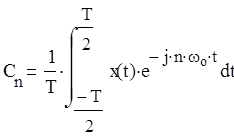
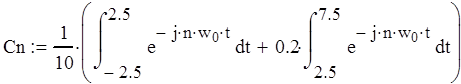
|C1|=0.255, |C2|=0, |C3|=0.085, |C4 |=0, |C5 |=0.051

Так как данная функция является четной, все коэффициенты b_n=0.

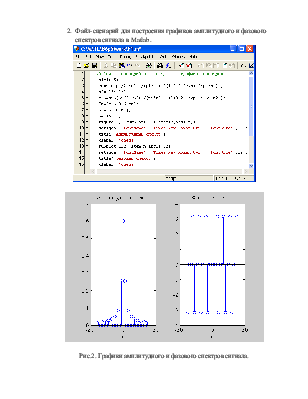
2.  Файл-сценарий для построения графиков амплитудного и фазового спектров сигнала в Matlab.

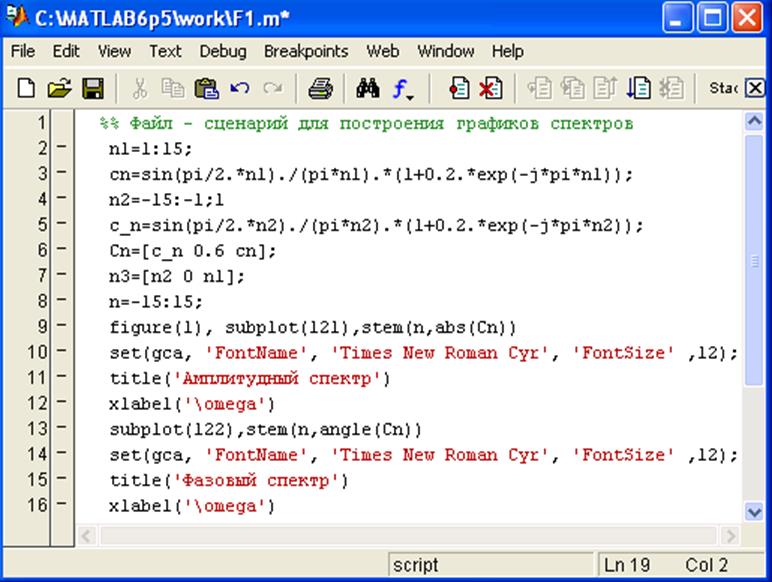
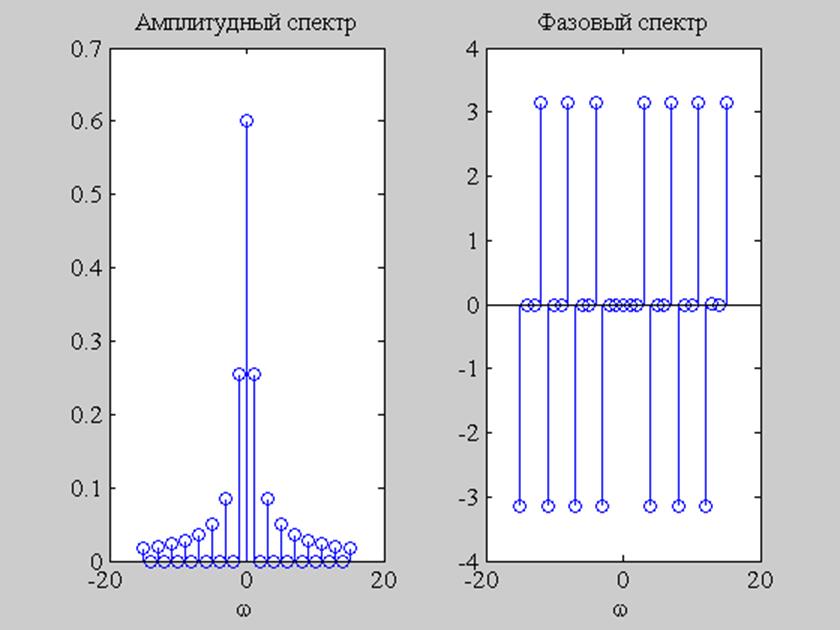
Рис.2. Графики амплитудного и фазового спектров сигнала.

3.  Определение спектра Фурье сигнала с помощью функции fft() Matlab.

%файл-сценарий для вычисления коэффициентов ряда Фурье  сигнала с помощью процедуры fft()

T=10;                                                          % период сигнала

t=-T:T/63:T;                                               % временной интервал

N=10;

x=0.4*square(2*pi*(t+2.5)./N,50)+0.6; % генерирование сигнала

figure(1);

subplot(311), plot(t,x)                      % график сигнала

xlabel('t')

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Прямоугольные импульсы')

axis([-10 10 0 1.2])

k=0:63;

% коэффициенты ряда Фурье

C= sin(pi/2.*k)./(pi*k).*(1+0.2.*exp(-j*pi*k));

Cn=[0,6 C];

n=2*k/T;

s=[0 n];

% график амплитудного спектра

subplot(312),

stem(s, abs(Cn));

xlabel('\omega')

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Амплитудный спектр')

axis([0 40 0 0.3])

y=fft(x,64);% Дискретное преобразование Фурье сигнала

% график ДПФ

subplot(313), stem(2*pi*k/T, abs(y)/64)

xlabel('\omega')

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Амплитудный спектр по команде fft()')

axis([0 40 0 0.7])

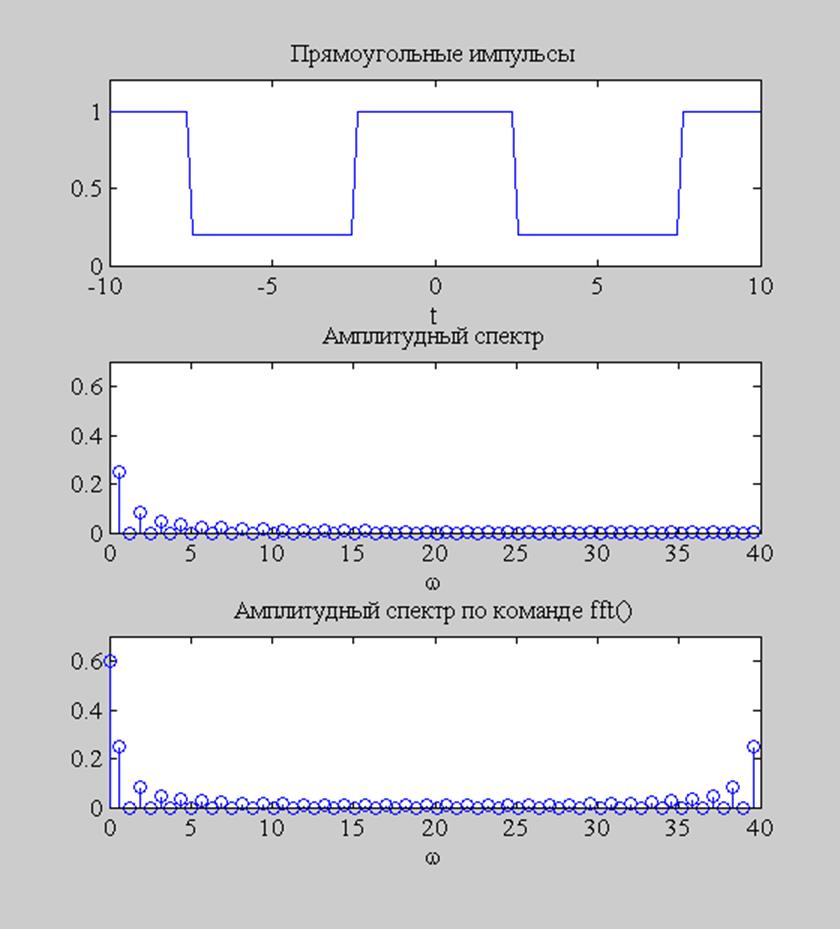
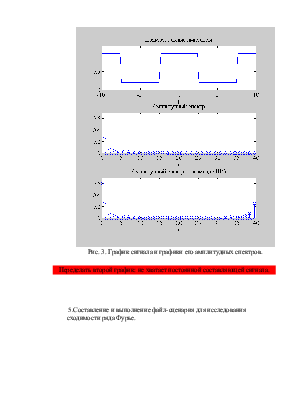
Рис. 3. График сигнала и графики его амплитудных спектров.

Переделать второй график: не хватает постоянной составляющей сигнала.

 5.Составление и выполнение файл-сценария для исследования сходимости ряда Фурье.

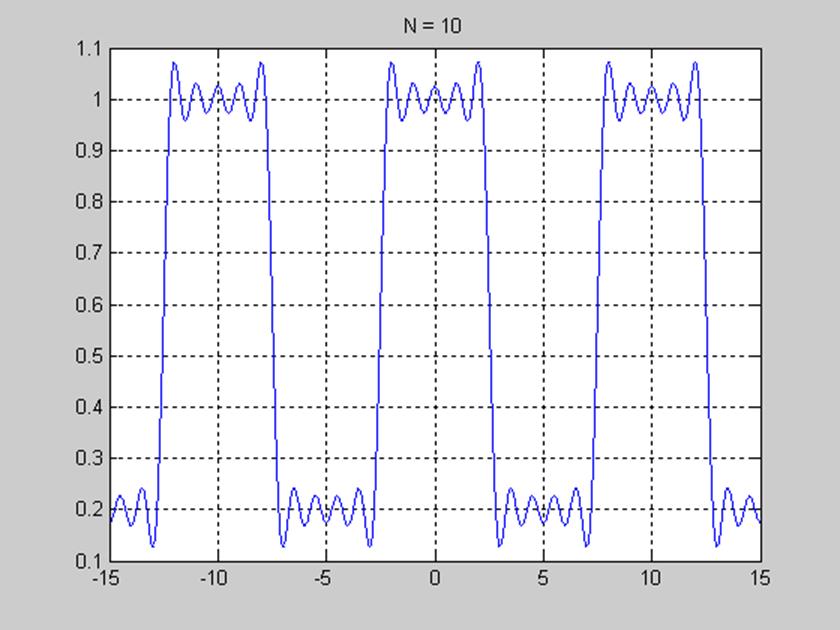
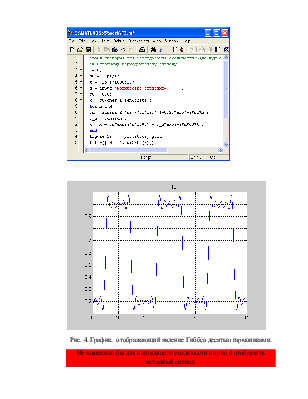
Рис. 4. График,  отображающий явление Гиббса десятью гармониками.

Не помешало бы для наглядности сходимости на рис.4 отобразить исходный сигнал.

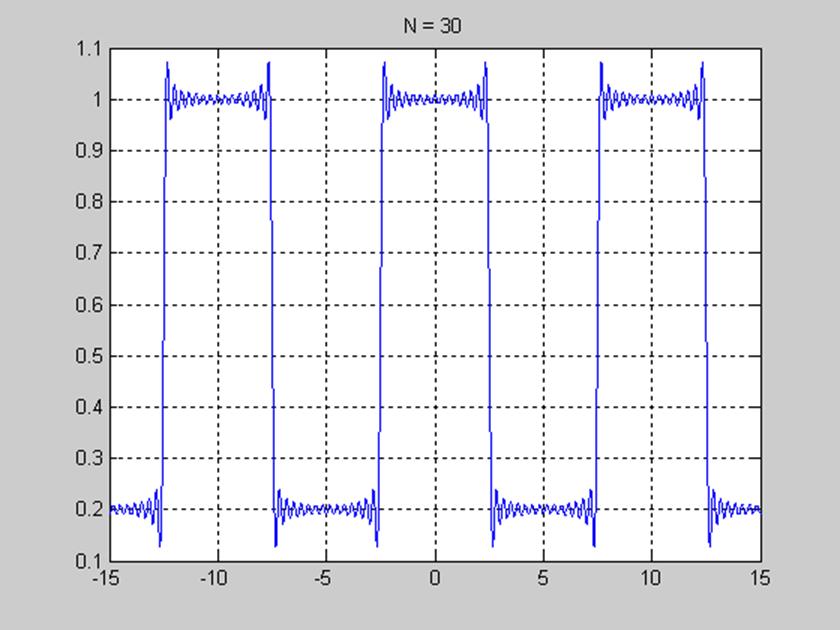
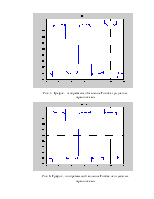
Рис. 5. График,  отображающий явление Гиббса тридцатью гармониками.

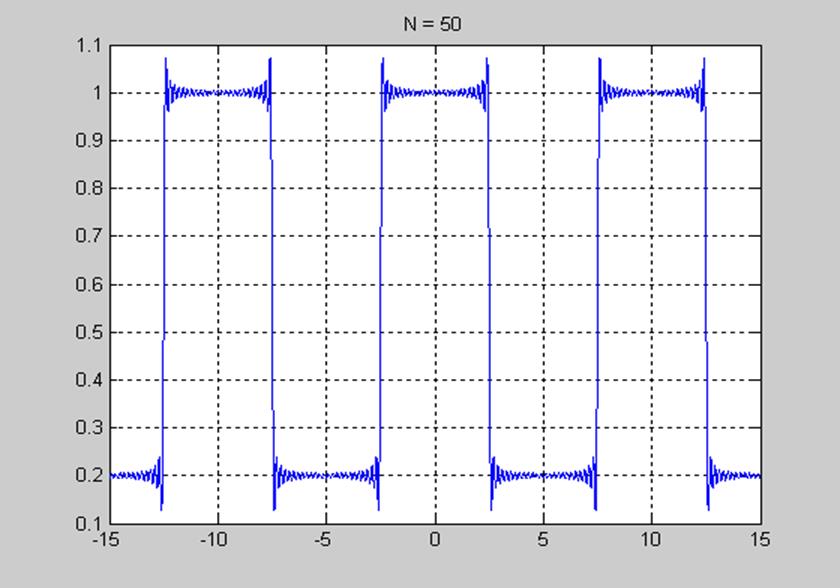
Рис. 6. График,  отображающий явление Гиббса пятидесятью гармониками.

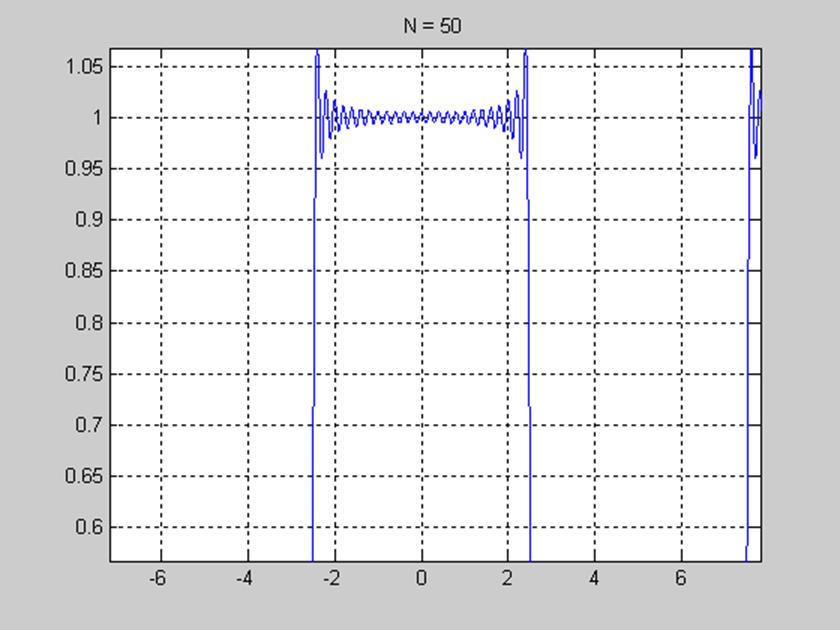
Рис. 7. График,  отображающий явление Гиббса пятидесятью гармониками (увелич. Масштаб).

Явление Гиббса – это явление связанное с появлением пульсации или выбросов при суммировании рядов Фурье. От числа гармоник N зависит число выбросов, амплитуда выбросов не зависит от числа гармоник.

 Отобразить свойства сходимости, рассмотрев среднеквадратичную сходимость и …

6. Аппроксимации сигналов: квадратной волны, ноты Ре, ноты До.

>> T=1/293.66;

>> w0 = 2*pi/T;

>> t = 0:1/8192:2;

>> x = zeros(1,length(t));

>> for n=1:2:19,

x = x + 4*sin(w0*n*t)/(pi*n);

end

>> y=harmonic(w0, 2*pi*8192, 2);

>> figure(1),plot(t(1:100),x(1:100),t(1:100),y(1:100)) , grid

>> axis([0 0.012 -1.5 1.5]);

>> p = zeros(1,length(t)); p=[x p y];

>> sound(p);

                                       Рис. 8. График аппроксимации ноты Ре.

>> T=1/261.63;

>> w0 = 2*pi/T;

>> do = zeros(1,length(t));

>> t = 0:1/8192:2;

>> k=[1 0.5 0.5 -0.3 0.2];

>> for n=1:5,

do = do + k(n)*sin(n*w0*t);

end

>> subplot(211), plot(t(1:100),do(1:100)) , grid

>> axis([0 0.012 -1.5 1.5]);

>> set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

>> title('График ноты До');

>> N=123; s=0:N;

>> y=fft(do,N+1);

>> subplot(212), stem(2*pi*s/T, abs(y)/(N+1)), grid

>> axis([0 max(2*pi*s/T)/2 0 max(abs(y)/(N+1))]);

>> set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

>> xlabel(' Угловая частота,  рад/сек')

>> title(' Амплитудный спектр ноты До по процедуре fft')

>> sound(do);

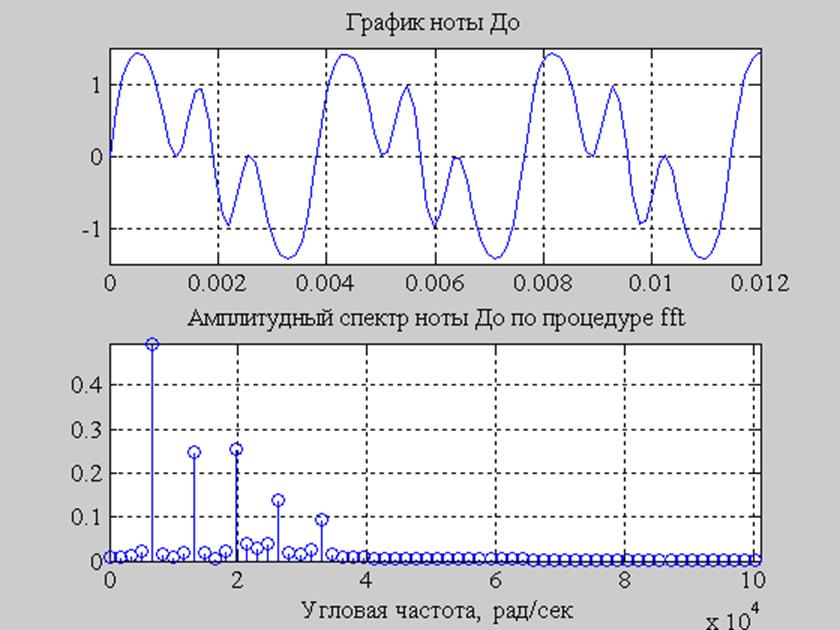
Рис.9. График ноты До и его амплитудный спектр.

Вывод: в данной работе было изучено спектральное представление периодических сигналов на примере периодической последовательности прямоугольных импульсов, при исследования сходимости ряда Фурье к исходному периодическому сигналу было рассмотрено явление Гиббса.

!!!Подробное описание основных моментов работы!!!

Удачи,Лёш!!!

JJJ